Interféromètre de Bath

Cette page sur l’interféromètre de Bath sera divisée en plusieurs parties :

Vous pouvez aller directement à la section qui vous intéresse en cliquant sur l’un des choix ci-dessous. Vous pourrez ensuite revenir directement ici avec la flèche retour de votre navigateur.

1 – Introduction à l’interférométrie
2 – Conception et construction du Bath
3 – Principales causes d’imprécisions
4 – Mise en œuvre du test
5 – Analyse des interférogrammes
6 – Ressources

Dans cette page, certaines photos et/ou illustrations sont « cliquables », c’est à dire qu’en cliquant sur elles cela la fera apparaître en plus grande taille. Pour distinguer celles qui sont cliquables de celles qui ne le sont pas, quand vous survolez une image, un dessin ou une vidéo avec votre curseur (généralement en forme de flèche) celui-ci prend alors la forme d’une main. Pour revenir à la page, cliquez sur la croix en haut à droite ou tapez sur la touche ESCAPE de votre clavier.

---

–

 

 

 

Introduction à l’interférométrie :

Nature ondulatoire de la lumière :

On sait aujourd’hui que la lumière a une double nature : corpusculaire et ondulatoire.

Pourtant, les savants ont longtemps pensé que la lumière était uniquement constituée de corpuscules se propageant en ligne droite.

Isaac Newton, déjà, avait mis en évidence un phénomène d’anneaux alternativement sombres et lumineux en disposant une lentille plan-convexe sur une lame plane réfléchissante (voir figure ci-dessous). Fervent partisan de la théorie corpusculaire de la lumière, il fut incapable de proposer une interprétation de ce phénomène.

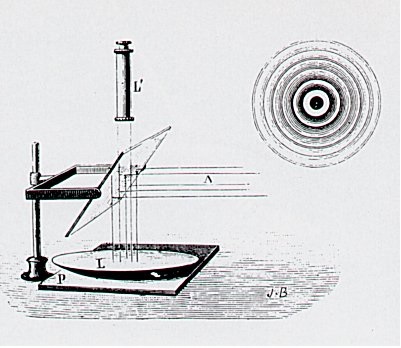Anneaux de Newton (livre II d’Optiks publié en 1704)

Il fallut attendre 1801 pour que Thomas Young apporte une preuve expérimentale de la nature ondulatoire de la lumière. En projetant une source lumineuse sur une plaque percée de deux trous de petite dimension, il obtint la formation de franges lumineuses sur un écran placé à l’arrière. Plus tard, les trous furent remplacés par des fentes pour accentuer la luminosité (voir figure ci-dessous).

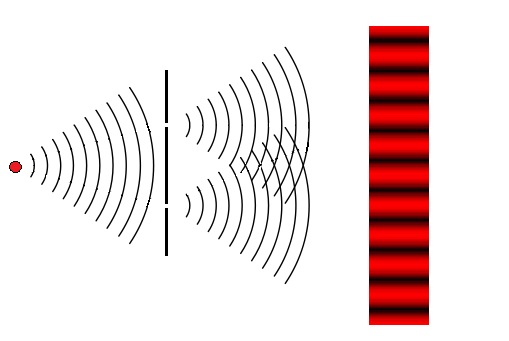Expérience des trous de Young (avec utilisation de fentes)

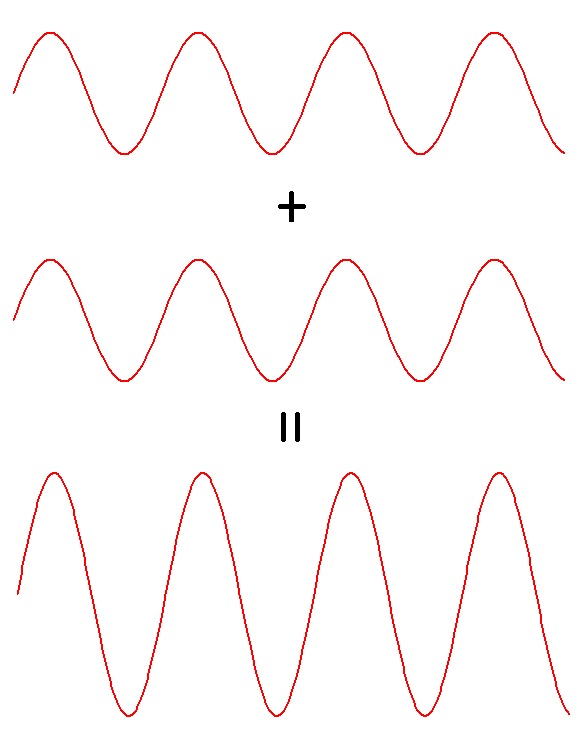
Les deux fentes éclairées par la source lumineuse se comportent comme deux sources produisant deux ondes lumineuses en phase. En fonction de la position considérée sur l’écran, on obtient une différence de marche variable entre ces deux ondes. Lorsque cette différence est nulle ou correspond à un multiple de longueur d’onde (figure ci-dessous à gauche) les maximums s’ajoutent et on obtient une bande lumineuse sur l’écran. Par contre, lorsque les ondes sont en opposition de phase (figure ci-dessous à droite), le maximum de l’une et le minimum de l’autre s’annulent en s’additionnant créant alors une bande sombre sur l’écran. On obtient ainsi une succession de bandes lumineuses et sombres que l’on appelle franges d’interférence.

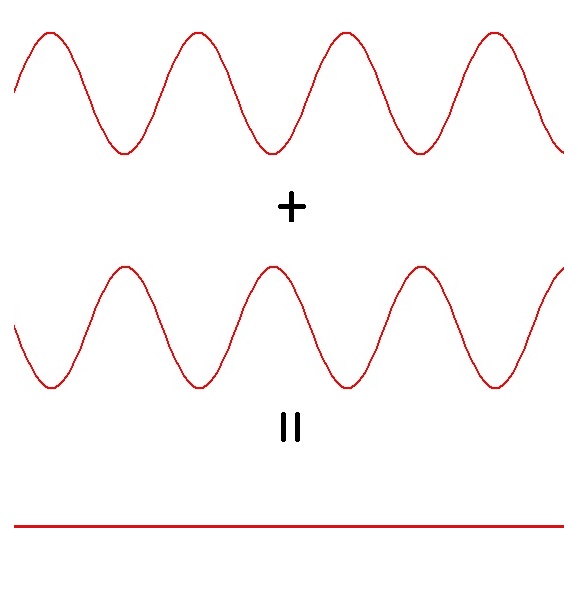Ondes en phase : Frange lumineuse	Ondes en opposition de phase : Frange sombre

 

 

 

Principe d’un interféromètre :

Le principe de l’interféromètre s’appuie sur ce phénomène d’interférences dû à la nature ondulatoire de la lumière. A partir d’une source lumineuse commune et de préférence monochromatique, on va faire interférer un front d’onde émergeant d’un miroir étalon (plan ou sphérique) et un front d’onde émergeant d’une pièce optique à tester (miroir ou lentille). Dans le cas d’un test d’une pièce plane, si cette dernière est optiquement « parfaite » (à l’identique de l’étalon), les franges apparaîtront parallèles (figure ci-dessous à gauche). Par contre, en présence d’un défaut, une ondulation de franges apparaîtra qui permettra de localiser et quantifier le défaut (figure ci-dessous à droite). Pour cela, on prend comme référentiel la distance séparant deux franges successives qui, dans le cas courant, correspond à la longueur d’onde de la source monochromatique (λ). On en déduit alors, par une simple règle de trois, la hauteur du renflement Δ correspondant au défaut optique sur l’onde (PTV : Peak to valley).

 

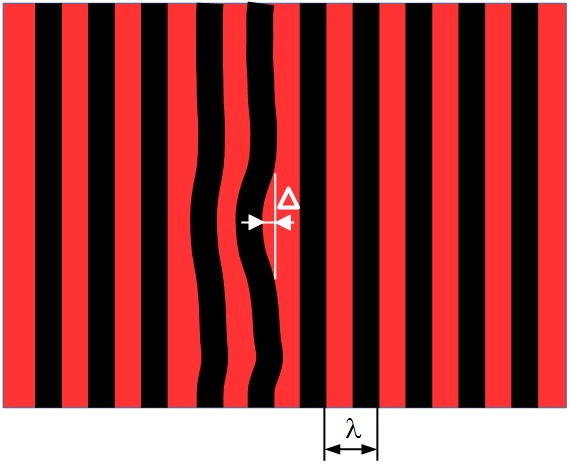Dans le cas de pièces optiques sphériques, les franges apparaissent circulaires et concentriques si centrées sur l’axe optique (voir figure ci-dessous).

Les algorithmes utilisés par les logiciels d’analyse d’interférogrammes vont, de la même manière, procéder à une mesure de l’écart entre les franges pour en déduire la position et l’amplitude des défauts sur l’onde. La plupart de ces algorithmes ne sont toutefois pas efficaces en présence de franges circulaires fermées (comme dans la figure ci-dessus). Pour optimiser l’analyse, un léger décalage (appelé tilt) sera opéré pour n’intégrer que les franges hors axe optique dont la forme courbe ne sera pas fermée ou trop prononcée. La figure ci-dessous à gauche montre un exemple d’interférogramme d’une pièce optique sphérique optimisé pour l’analyse. La figure ci-dessous à droite donne l’aspect d’un interférogramme d’une pièce optique asphérique. Dans ce dernier cas, la déformation des franges est due à l’aberration sphérique dont les caractéristiques devront être prises en compte par le logiciel.

 

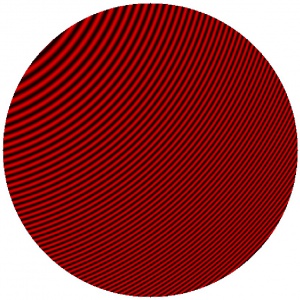Différents types d’interféromètres :

On doit à Hippolyte Fizeau la conception du premier interféromètre qui porte aujourd’hui son nom. Il en décrit les principes en 1850 alors qu’il cherchait par ce moyen à mesurer la vitesse de la lumière. Le concept général de l’interféromètre de Fizeau est le suivant (cas d’un test de miroir plan) :

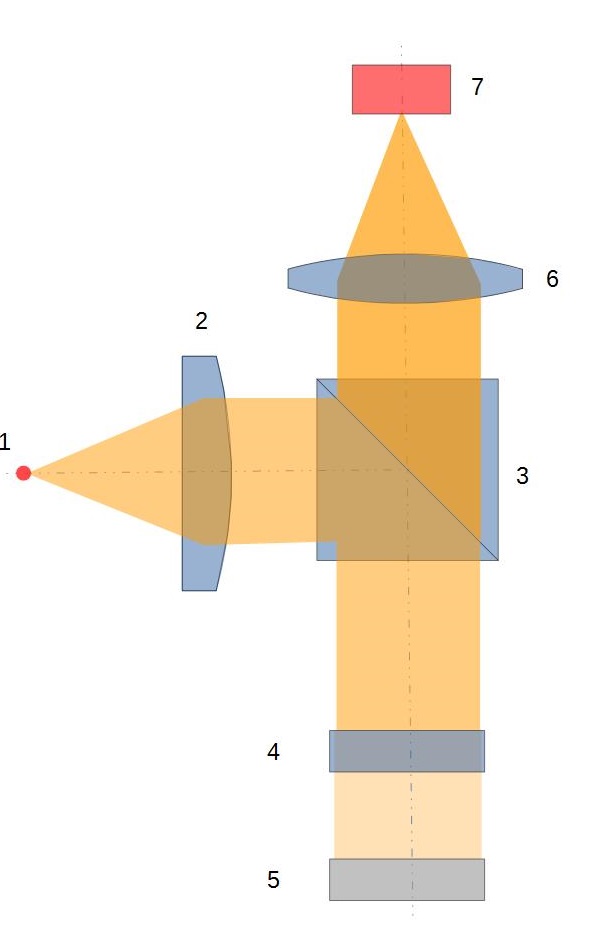
Une source lumineuse (de préférence monochromatique) (1) émet des fronts d’ondes sphériques vers un collimateur (2) dont le rôle est de les transformer en fronts d’ondes plans sur un diamètre de pupille adapté au test. Ce faisceau rencontre un cube séparateur (3) qui le réfléchit en partie vers un miroir étalon (4) dont la forme est très précise et de même nature que la pièce optique à tester (plane dans le cas présent). Ce plan étalon étant semi-réfléchissant, une partie du faisceau va subir une réflexion et être renvoyé vers un objectif (6) afin de former une première image sur le capteur de l’imageur (7). L’autre partie du faisceau va traverser l’étalon (4) et se réfléchir sur le miroir à tester (5). Il va ensuite former une nouvelle image sur le capteur (7) de la même manière que le premier faisceau. En formant un léger angle entre la surface de l’étalon (4) et du miroir testé (5) on va générer des différences de marche sur les deux fronts d’ondes émergents et créer ainsi des franges d’interférence mettant en évidence les écarts de forme entre le miroir testé et l’étalon. Un miroir sphérique concave peut être mesuré de la même manière en utilisant un étalon de forme identique.

Albert Abraham Michelson reprit les travaux de Fizeau en améliorant son concept d’interféromètre. On retrouve en effet dans l’interféromètre de Michelson des configurations communes à celles du modèle de Fizeau :

Un front d’onde plan est également généré par une source (1) reprise par un collimateur (2) dont le faisceau est réfléchi en partie sur un cube séparateur (3) vers un plan étalon (4). Ce dernier réfléchit le faisceau en direction de l’imageur (7) via son objectif (6). La différence avec le concept de Fizeau réside essentiellement dans le fait que la pièce optique à tester (5) n’est pas située sur le même axe que celui de l’étalon (axes perpendiculaires). La partie du faisceau source non réfléchie par le cube séparateur (3) va donc traverser ce dernier pour atteindre la pièce à tester (5) sur laquelle elle va se réfléchir et atteindre le système imageur (6) et (7) par réflexion dans le cube séparateur (3). Les interférences entre les deux front d’ondes captés par l’imageur vont permettre d’analyser la forme de la pièce optique testée. Des dispositifs de réglage fin de l’orientation et de translation des pièces (4) et (5) permettent d’obtenir des franges en nombre et forme optimisés.

A partir de ces concepts de base, plusieurs types d’interféromètres ont été conçus par la suite. On peut notamment citer les interféromètres de Twyman-Green, Mach-Zehnder, et Sagnac.

 

Cas particulier de l’interféromètre de Bath :

C’est en 1973 que Karl-Ludwig Bath publie un article sur un concept d’interféromètre dérivé du modèle de JW Gates (voir chapitre  “Ressources” – “Optical shop testing” de Daniel Malacara).

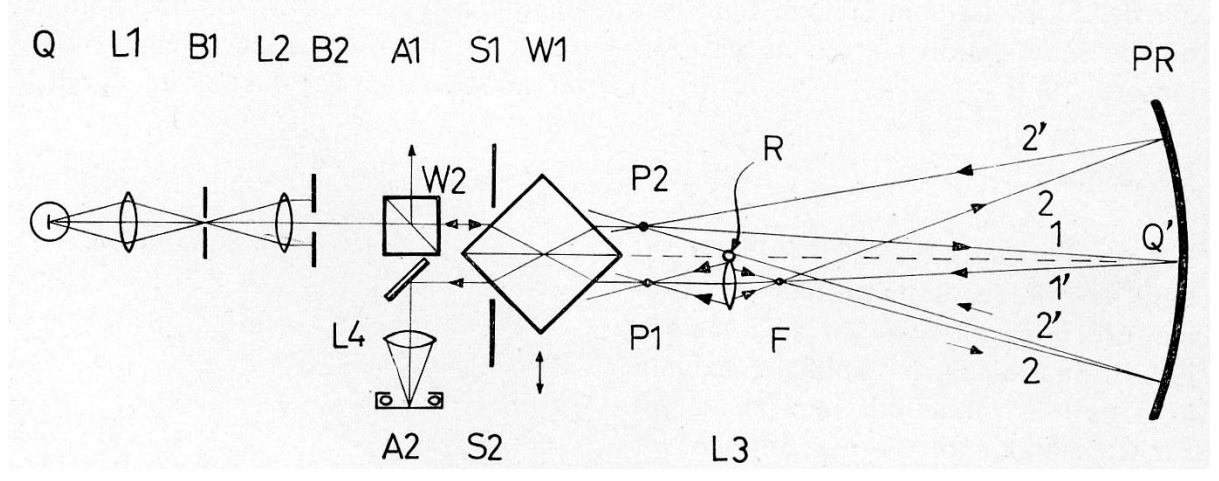Schéma tiré de l’article original paru en 1973 dans la revue « Sterne und weltraum » (voir chapitre “Ressources”)

L’inconvénient majeur des interféromètres de Fizeau et Michelson, notamment pour l’amateur, réside dans le coût élevé de la pièce étalon. En effet, cette dernière  doit avoir au moins la même dimension et la même forme que la pièce à contrôler tout en respectant des critères de qualité optique particulièrement élevés. L’idée pour le moins innovante de Karl-Ludwig Bath consiste à utiliser une partie de la pièce optique à tester pour produire un front d’onde de référence comme le ferait un étalon classique. On peut enfin noter que cet interféromètre n’est adapté qu’au contrôle de miroirs concaves.

Le principe général en est le suivant :

Pour faciliter la compréhension des schémas, on décrira alternativement les chemins du faisceau de référence et du faisceau testé.

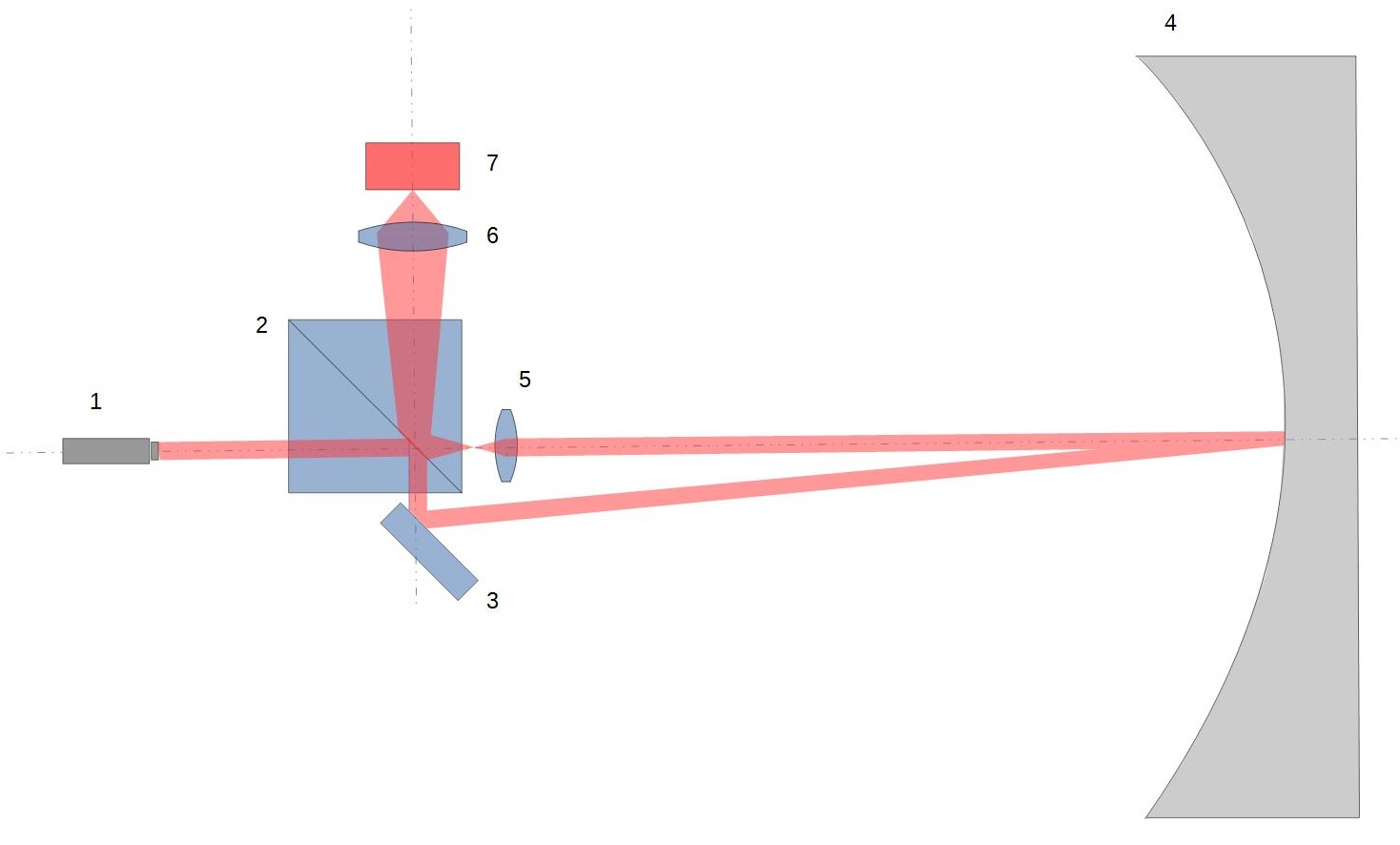Interféromètre de Bath : Chemin du faisceau de référence

La source monochromatique est constituée d’un laser (1) produisant un faisceau collimaté (non divergent, non convergent) de quelques millimètres de diamètre. Celui-ci est en partie réfléchi par le cube séparateur (2) puis dirigé vers un petit miroir plan (3) dont l’orientation va  permettre de pointer le faisceau dans la région centrale du miroir à contrôler (4). On peut à ce stade poser un postulat : Étant donné la faible surface interceptée par le faisceau sur le miroir, on peut considérer celle-ci comme optiquement proche de la perfection. En effet, dans les cas courants, les gros défauts de forme ont des largeurs de plusieurs centimètres et n’altèrent donc pas significativement un faisceau de quelques millimètres de diamètre. C’est cette caractéristique qui donne à l’interféromètre de Bath tout son intérêt pratique. Le faisceau réfléchi par le miroir testé (4) est donc « porteur » d’un front d’onde de référence quasi-parfait. Il va ensuite rencontrer une lentille convergente (5) de courte focale qui va le concentrer puis le déployer. Ce faisceau divergent va ensuite être partiellement réfléchi par le cube séparateur (2) et être dirigé vers le système imageur (6) et (7) dans lequel il va  matérialiser le front d’onde de référence.

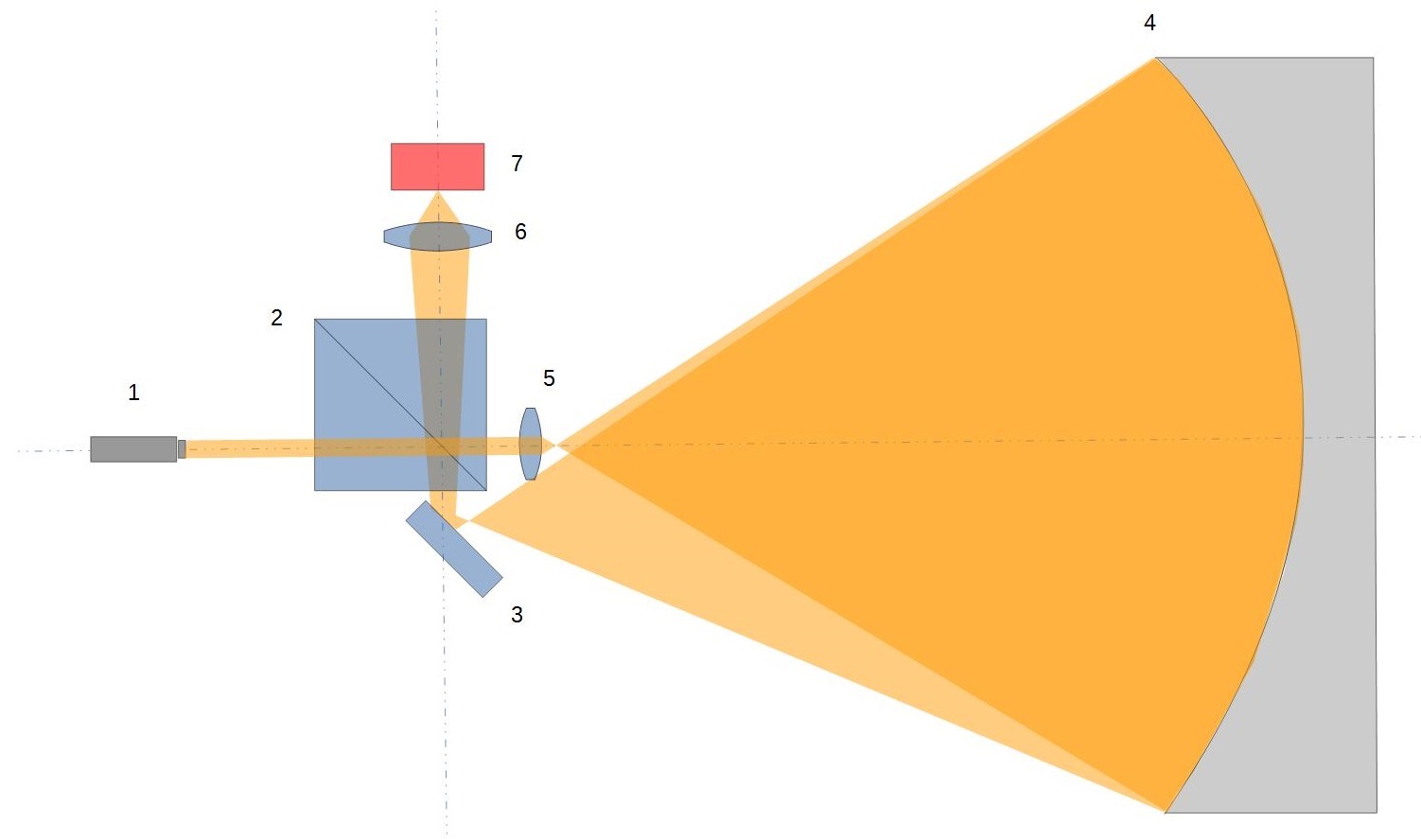Interféromètre de Bath : Chemin du faisceau testé

 

La partie du faisceau laser (1) qui n’est pas réfléchie par le cube séparateur (2) traverse ce dernier pour atteindre la lentille convergente (5). A la sortie de cette dernière, le faisceau se focalise puis se déploie pour couvrir toute l’ouverture du miroir à tester (4) contrairement au faisceau de référence décrit précédemment. Le faisceau réfléchi sur le miroir est donc porteur d’un front d’onde qui est quant à lui altéré par les défauts optiques de la surface à tester. Celui-ci va ensuite se « focaliser » en direction du petit miroir plan (3) et être réfléchi vers le système imageur pour former le front d’onde testé.

La superposition des plages de fronts d’ondes de référence et testé va générer des franges d’interférences. Des mouvements fins en tilt et focus vont permettre d’optimiser le nombre et la forme des franges pour une analyse par un logiciel spécifique.

L’interféromètre de Bath fait partie de la catégorie « à chemin commun » (ou common-path en anglais) dans la mesure où les faisceaux de référence et testé empruntent le même trajet ce qui constitue, on le verra plus loin, un atout non négligeable.

On peut mentionner différentes configurations de l’interféromètre de Bath ayant in fine des performances équivalentes.

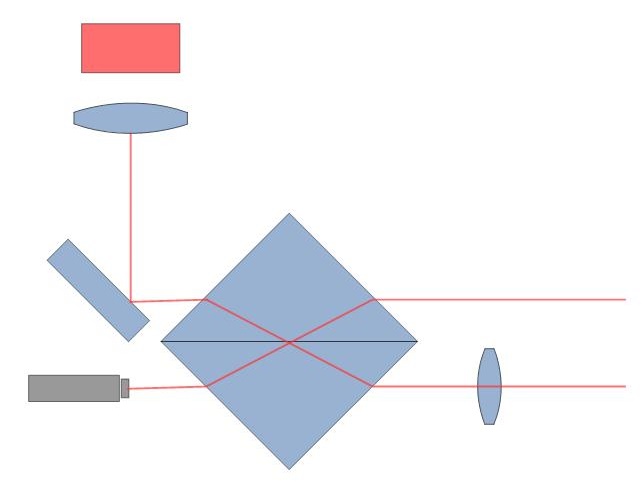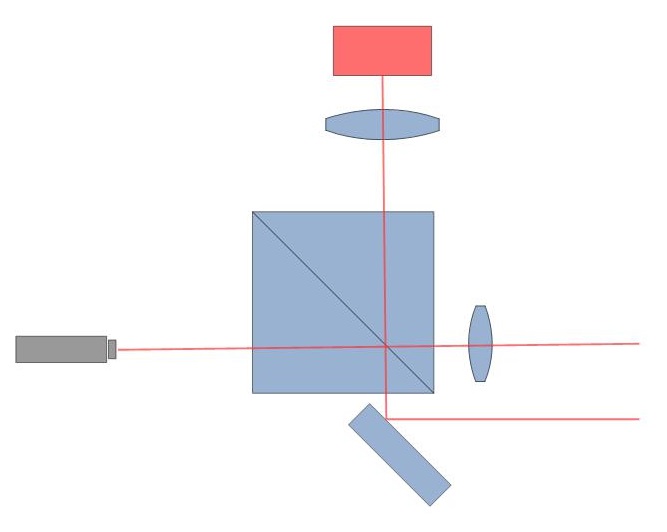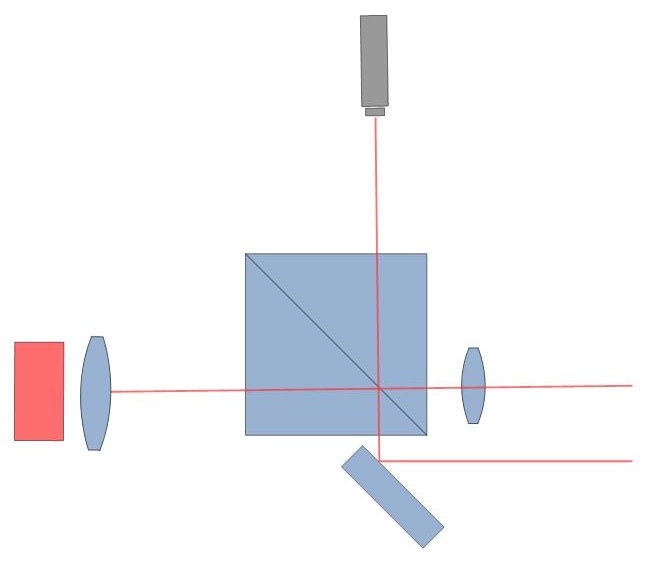• Le modèle droit (image de gauche) : C’est la configuration originale proposée par Karl-Ludwig Bath. Elle utilise les propriétés de réfraction et de réflexion du cube séparateur. Il n’est pas nécessaire ici que les intensités de flux par transmission et par réflexion soient équivalentes.
• Le modèle à angle droit (image du milieu) : C’est la configuration la plus répandue. Les alignements optiques sont peut-être plus intuitifs que dans la configuration précédente. Un équilibrage 50% / 50% des flux transmis et réfléchis est ici requis pour le cube séparateur.
• Variante du modèle à angle droit (image de droite) : Tout-à-fait équivalente à la précédente, cette configuration peut offrir quelques avantages ergonomiques (Appareil photo en ligne par exemple).

---

–

 

 

 

Conception et construction du Bath :

 

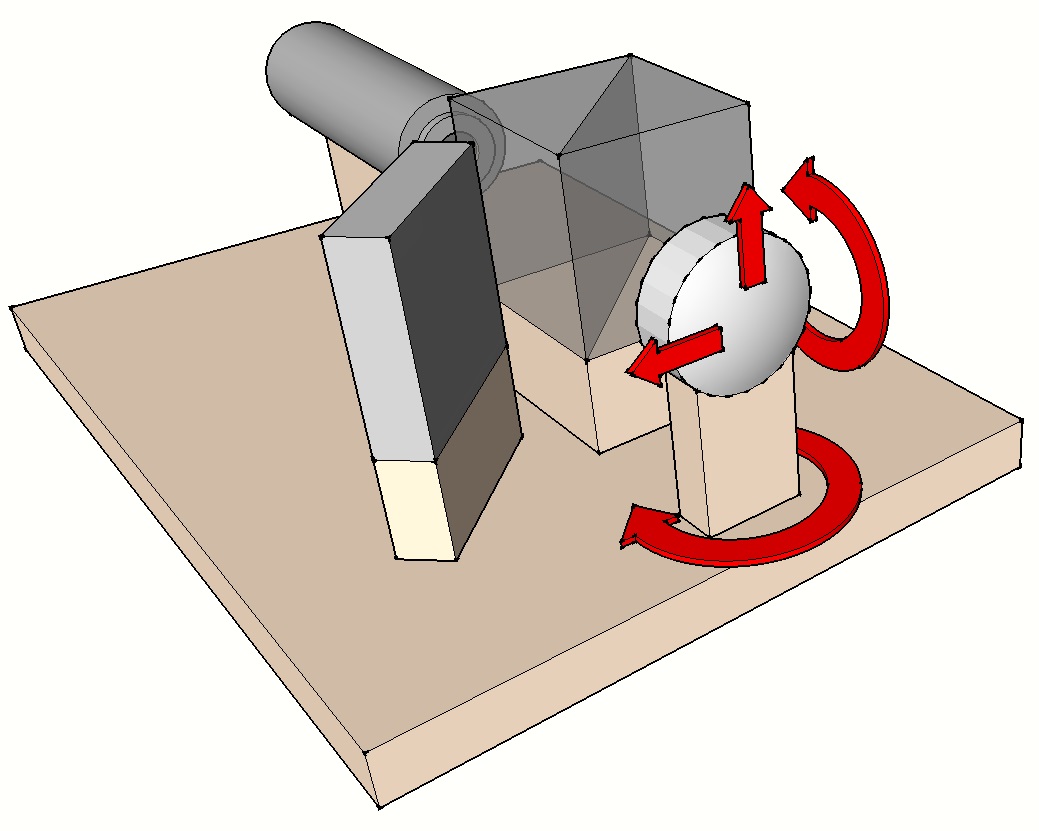
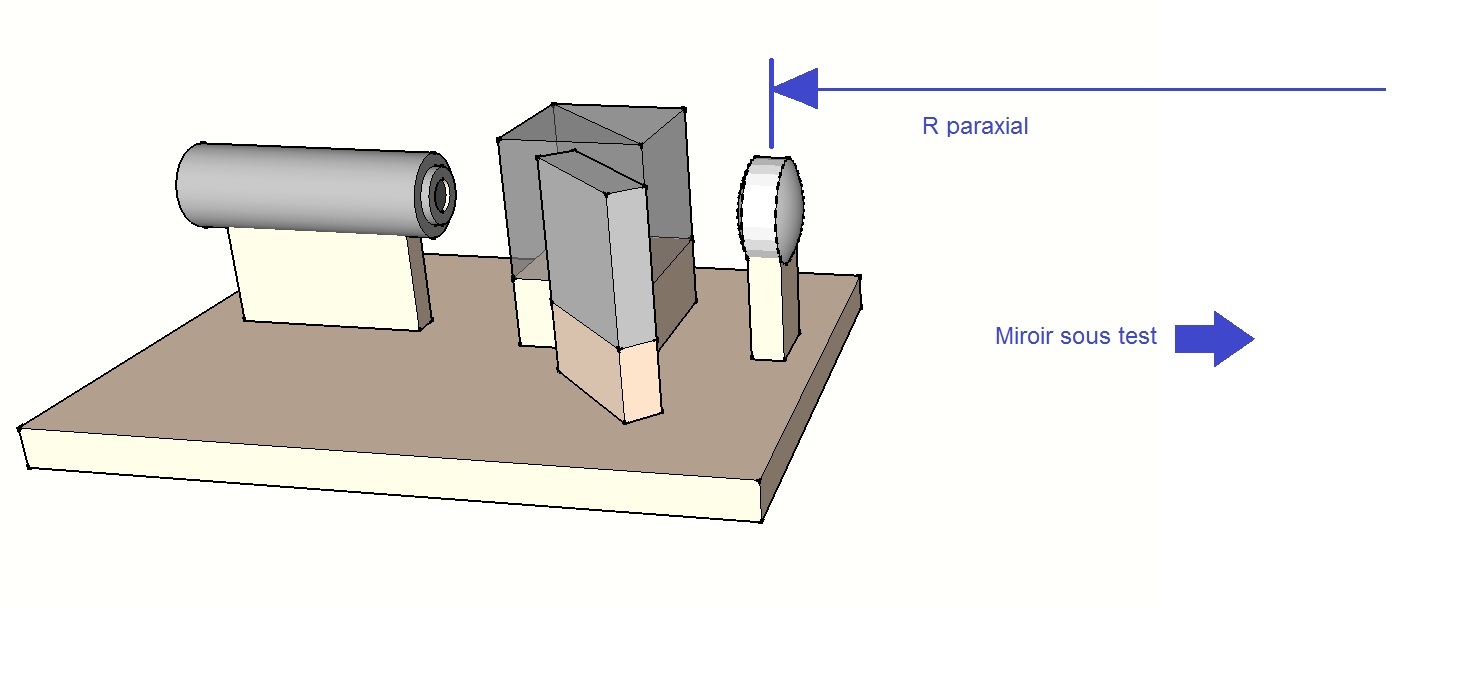
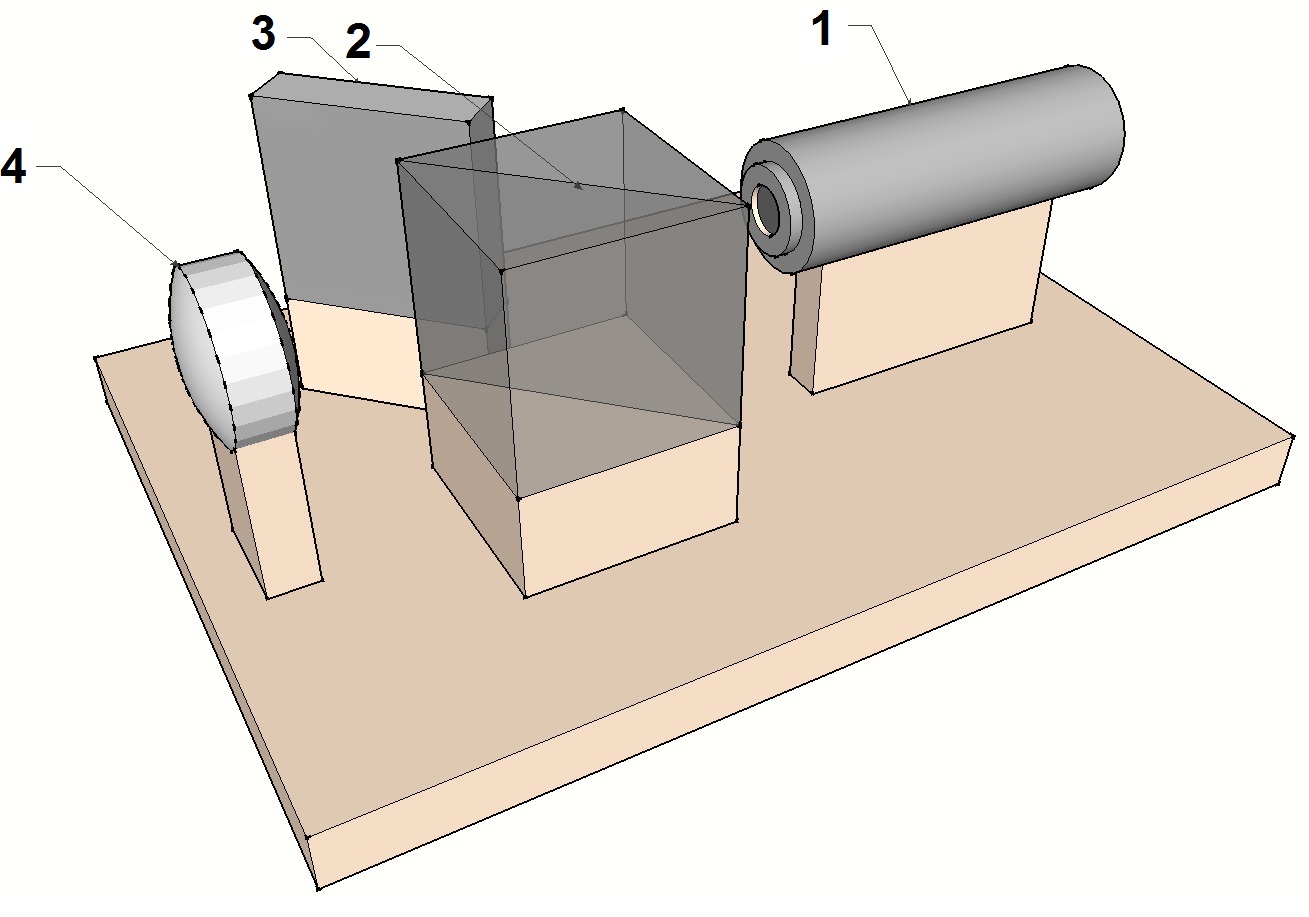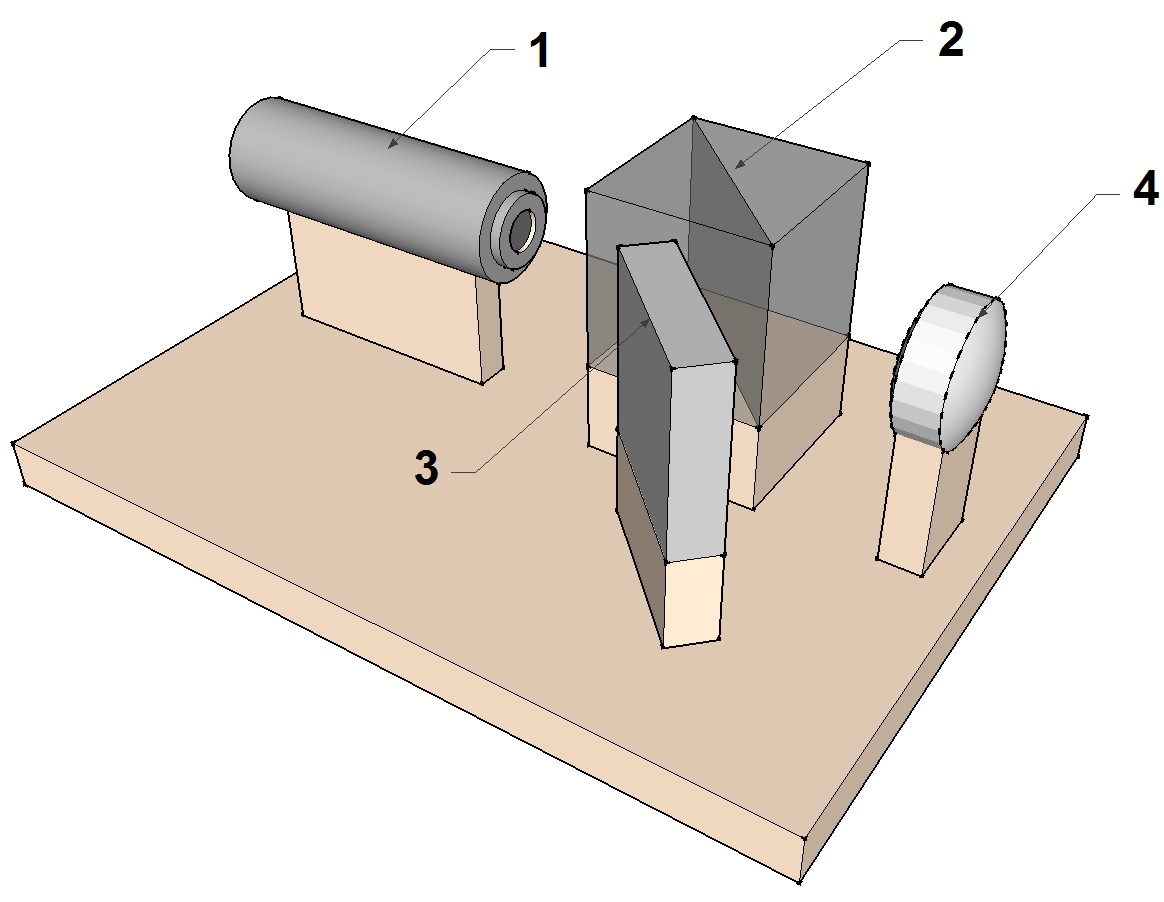
• Les figures ci-dessus représentent les différents composants de l’interféromètre de Bath (sauf le dispositif imageur qui n’est pas matérialisé). Ceux-ci sont fixés sur un socle avec possibilité de réglages fins qui seront décrits plus loin. Ils sont constitués d’une source laser (1), d’un cube séparateur (2), d’un miroir plan (3) et d’une lentille convergente (4).

Voyons en détail les caractéristiques de chacun de ces composants :

 

Source laser :

La source laser est adaptée pour l’interférométrie en raison de ses caractéristiques : cohérence de l’onde (spatiale et temporelle), monochromatique (pour un meilleur contraste) et collimatée. Des pointeurs laser économiques peuvent être utilisés. On leur préférera toutefois des modules laser d’un certain niveau de qualité ayant notamment les caractéristiques suivantes :

• Lentille en verre (les pointeurs sont quant à eux généralement équipés de lentilles en plastique). Les lentilles de mauvaise qualité ont tendance à créer des artefacts dans les interférogrammes. On peut envisager le remplacement de la lentille plastique d’un laser bas de gamme par une lentille en verre de récupération mais cette adaptation n’est toutefois pas aussi triviale qu’il n’y paraît.
• Lentille focusable : Cette mise au point permet de collimater au mieux le faisceau dont la divergence doit être limitée.
• Précision de la longueur d’onde : Les lasers bas de gamme ne garantissent généralement pas la longueur d’onde avec grande précision. Cette donnée entre dans le calcul de la précision du miroir testé et doit donc être connue avec une tolérance relativement faible. Il existe certes des méthodes assez simples pour mesurer la longueur d’onde d’un laser mais avec une précision toute relative (voir exemple ici).

Exemple de module laser (Picotronic)

Pour information, on peut également citer le cas des lasers à gaz hélium-néon (He-Ne). Ce type de laser, souvent utilisé dans les laboratoires, émet une onde de haute qualité à 632,8 nanomètres. Toutefois, sa taille et surtout son coût les rendent peu appropriés à l’usage de l’amateur.

Concernant la longueur d’onde, le choix se porte généralement sur des lasers verts ou rouges qui présentent chacun des avantages et inconvénients :

• Le laser vert (l = 532 nm) est plus lumineux que le rouge et les capteurs des imageurs numériques sont plus sensibles à cette longueur d’onde. Son intensité lumineuse n’est pas réglable. Son coût est plus élevé que le rouge. Son faisceau est de section circulaire.

Le laser rouge (l = 635 à 650 nm) est plus économique. Il est possible de régler son intensité lumineuse en le faisant atteindre son seuil de « lasing » sous lequel il se comporte comme une diode classique par perte de cohérence de l’onde. Pour effectuer ce réglage, on peut utiliser un module d’alimentation à tension de sortie variable (en kit ou déjà monté). Par ailleurs, les modules (ou pointeurs) laser étant particulièrement consommateurs de piles, l’utilisation d’une alimentation permanente garantit un confort durant les tests.

Module d’alimentation à tension variable (Conrad Electronique)

 

Le faisceau est généralement de section rectangulaire. Cette caractéristique s’avère intéressante pour l’optimisation de l’orientation du faisceau en rapport avec la polarisation de l’onde émise (voir chapitre « Mise en œuvre du test »).

Concernant la puissance, un laser de 1mW (classe 2) devrait être suffisant pour obtenir le flux lumineux requis. Dans certains cas (par exemple pour un miroir non aluminé), une puissance de 5mW (classe 3R) peut s’avérer utile. On peut également jouer sur le temps d’exposition lors de la prise de vue.

Attention : les lasers de classe 3 et plus peuvent provoquer des lésions oculaires graves (voir ici les recommandations d’usage).

Enfin, le diamètre du faisceau ne doit pas être trop faible pour garantir un déploiement en sortie de lentille convergente couvrant la totalité du miroir à contrôler. L’optimisation du diamètre de faisceau est à déterminer en corrélation avec la longueur focale de la lentille (voir paragraphe « Lentille convergente » ci-dessous). Certains types de laser (notamment He-Ne) ont des faisceaux particulièrement fins qui nécessitent l’adjonction d’un expanseur optique pour en élargir le diamètre.

La conception du support de la source laser doit idéalement prévoir les degrés de liberté suivants :

 

Des rotations selon un axe vertical et un axe horizontal pour un réglage de l’alignement du faisceau sur le cube séparateur et l’axe de la lentille. Une rotation du laser sur son axe pour permettre l’équilibrage de l’intensité lumineuse des 2 faisceaux émergeant du cube séparateur rendu nécessaire du fait de la nature polarisée de l’onde laser.

 

Cube séparateur :

On choisira un cube avec une répartition de l’intensité lumineuse de 50% par transmission et 50% par réflexion. Un traitement antireflet est souhaitable. Le cube introduit une polarisation des faisceaux qui le traverse. Loin de constituer un problème, on pourra dans certains cas tirer parti de ce phénomène (voir chapitre “Mise en œuvre du test”).

Exemple de cube séparateur

On limitera généralement la dimension du cube entre 10 et 15 mm de côté. En effet, le cube étant attaqué par des faisceaux dont l’angle des rayons est variable (cônes de lumière), il peut se produire une aberration sphérique du fait de la réfraction qui sera d’autant plus prononcée que l’épaisseur de verre traversée sera importante, l’ouverture du cône de lumière ouvert et son diamètre sur  les faces du cube large. Dans les conditions courantes d’utilisation, l’influence de ce défaut reste toutefois négligeable.

On peut également fabriquer un cube séparateur à l’aide de deux prismes collés au baume du Canada.

Les mouvements à prévoir pour le cube séparateur se limitent à un seul degré de liberté :

Une rotation unique selon un axe vertical est suffisante pour effectuer les réglages.

Elle sert à rejeter des reflets parasite hors du champ de l’interférogramme (voir chapitre « Mise en œuvre du test »).

 

Miroir plan :

Un miroir de petite dimension est tout à fait suffisant compte-tenu du faible diamètre des faisceaux qu’il doit réfléchir. Peu importe sa forme également (carrée ou ronde). Il doit bien sûr être métallisé pour ne pas perdre d’intensité lumineuse lors de la réflexion des faisceaux.

Un petit prisme peut également assurer cette fonction.

Les degrés de liberté à prévoir pour le miroir sont les suivants :

Deux rotations selon des axes perpendiculaires. Ces mouvements servent au réglage du parallélisme des faisceaux.

 

Lentille convergente :

Une lentille biconvexe (ou à défaut double-convexe si les courbures de chaque dioptre ne sont pas trop différentes) semble être la solution la plus adaptée. Une lentille plan convexe peut également être utilisée mais elle peut générer plus d’aberration sphérique dans certaines configurations. Le diamètre de la lentille doit être suffisant pour ne pas diaphragmer le faisceau tout en gardant un peu de marge. A l’inverse, il ne doit pas être surdimensionné au risque d’empiéter sur le deuxième faisceau (voir paragraphe « Positionnement des composants » ci-dessous). On évitera également les supports et autres montures de la lentille qui pourraient déborder sur l’autre faisceau. De ce point de vue, l’utilisation d’un oculaire n’est pas d’un usage très adapté.

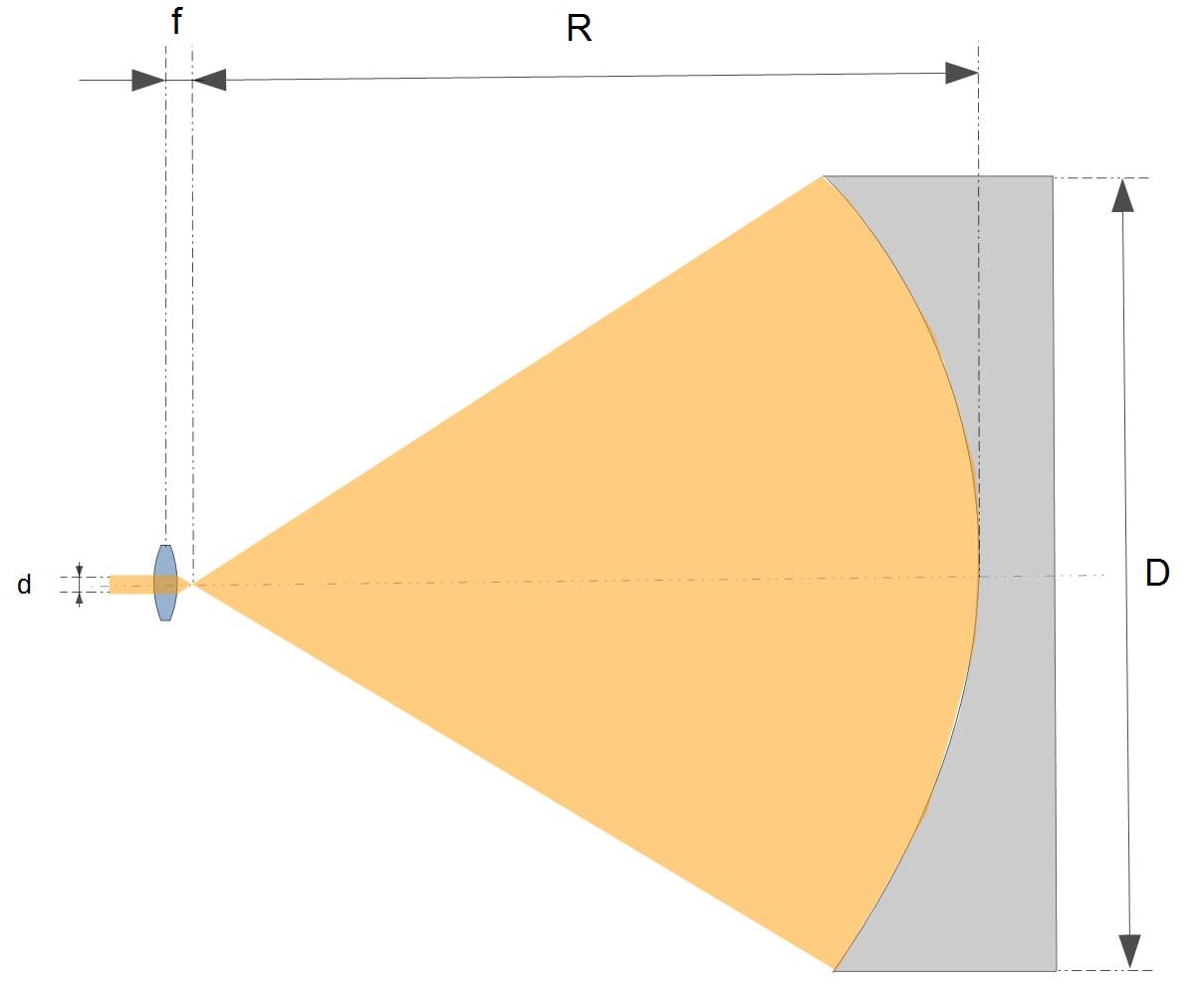
Le choix de la focale doit être optimisé en fonction du diamètre du faisceau laser, du diamètre du miroir à tester et de son rayon de courbure. L’objectif est de couvrir largement le diamètre du miroir testé avec le faisceau déployé (voir figure ci-dessous).

On peut ainsi poser la relation suivante :

f / d  << R / D

avec f = longueur focale de la lentille
d = diamètre du faisceau laser (ou plus petite dimension du spot s’il est de forme rectangulaire)
R = rayon de courbure du miroir testé
D = Diamètre optique du miroir testé

La qualité du faisceau laser n’étant en général pas homogène jusqu’en bord de champ, il est conseillé de prendre de la marge sur son rapport d’ouverture en respectant par exemple la relation suivante :

f / d  = 1/2 (R / D)

Par exemple, pour tester un miroir à F/D = 4 (soit R/D = 8) avec un laser dont le faisceau fait 5 mm de diamètre, on choisira de préférence une lentille de 20 mm maximum de longueur focale.

Il ne faut pas non plus tomber dans l’excès inverse en ouvrant trop largement le faisceau de test au risque de perdre une quantité importante du flux lumineux après réflexion.

Vu le faible coût de ce composant optique, on peut faire en sorte de disposer de 2 ou 3 lentilles interchangeables avec des longueurs focales échelonnées et optimisées pour différents rapports d’ouvertures de miroirs.

Idéalement, les degrés de liberté à prévoir pour la lentille sont les suivants :

Deux rotations selon des axes perpendiculaires et deux translations. La mise en place de quatre degrés de liberté peut sembler excessive mais l’expérience montre qu’ils ne sont pas de trop pour peaufiner le centrage du faisceau et limiter au maximum le tilt (non perpendicularité de la lentille par-rapport à l’axe du faisceau laser). Cela dit, les translations sont plus utiles que les rotations dans la plupart des cas.

 

Appareil photo :

L’appareil photo doit être équipé d’un objectif répondant à certains critères :

• Sa pupille d’entrée doit être suffisante pour ne pas diaphragmer les faisceaux émergents.
• Sa qualité optique doit permettre de limiter les aberrations (notamment la distorsion) afin de produire des interférogrammes les moins déformés possibles pour une analyse précise du front d’onde. Généralement, les objectifs à focale fixe répondent mieux à ces critères (voir paragraphe « Qualité des composants optiques » ci-dessous).
• Sa focale doit être suffisante pour garantir une résolution d’au moins 640 x 640 pixels pour la partie utile de l’interférogramme. Une focale de 80 à 100 mm sur un appareil reflex numérique satisfait généralement à cette exigence.

Il est possible d’imager les interférogrammes sans objectif mais cette piste est à déconseiller fortement en raison des effets de la diffraction qui dégradent notablement l’image, notamment au bord du miroir (voir exemple ici).

Concernant la fonction de mise au point, il est quasiment indispensable de pouvoir débrayer l’autofocus et de procéder en mode manuel (via la bague ou une commande déportée).

Les degrés de liberté nécessaires au réglage du positionnement de l’appareil photo sont deux rotations (selon des axes perpendiculaires) et deux translations :

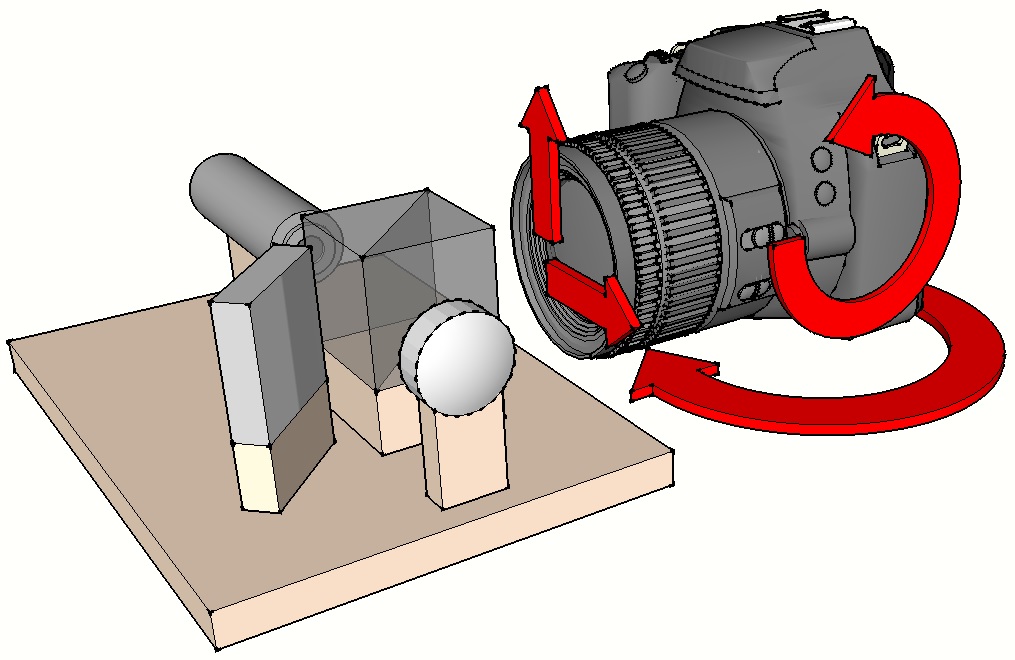
Ces réglages permettent de collimater un mieux l’appareil photo afin de garantir une qualité optimale des interférogrammes. On limitera ainsi :

• Les aberrations hors axes liées à un décentrage du faisceau sur l’objectif
• Le vignetage causé par le diaphragme
• Le tilt (plans de l’image et de la matrice formant un angle). Celui-ci peut générer de l’ovalisation des plages de l’interférogramme et une mise au point non homogène sur la totalité de la circonférence du miroir.

L’utilisation d’un pied photo peut permettre d’effectuer ce positionnement. Toutefois, pour un réglage plus fin et plus stable, on peut s’orienter vers une solution de support solidaire de l’interféromètre équipé de glissières (translations) et de réglages d’assiette.

L’ensemble doit être conçu de telle manière que la distance entre l’objectif et le cube soit minimale (notamment pour limiter le vignetage).

 

Positionnement des composants :

Pour la conception et la fabrication de l’interféromètre, la réalisation d’une épure à grande échelle constitue une aide précieuse. On peut également utiliser une feuille de calcul avec traçage des rayons telle que celle-ci :

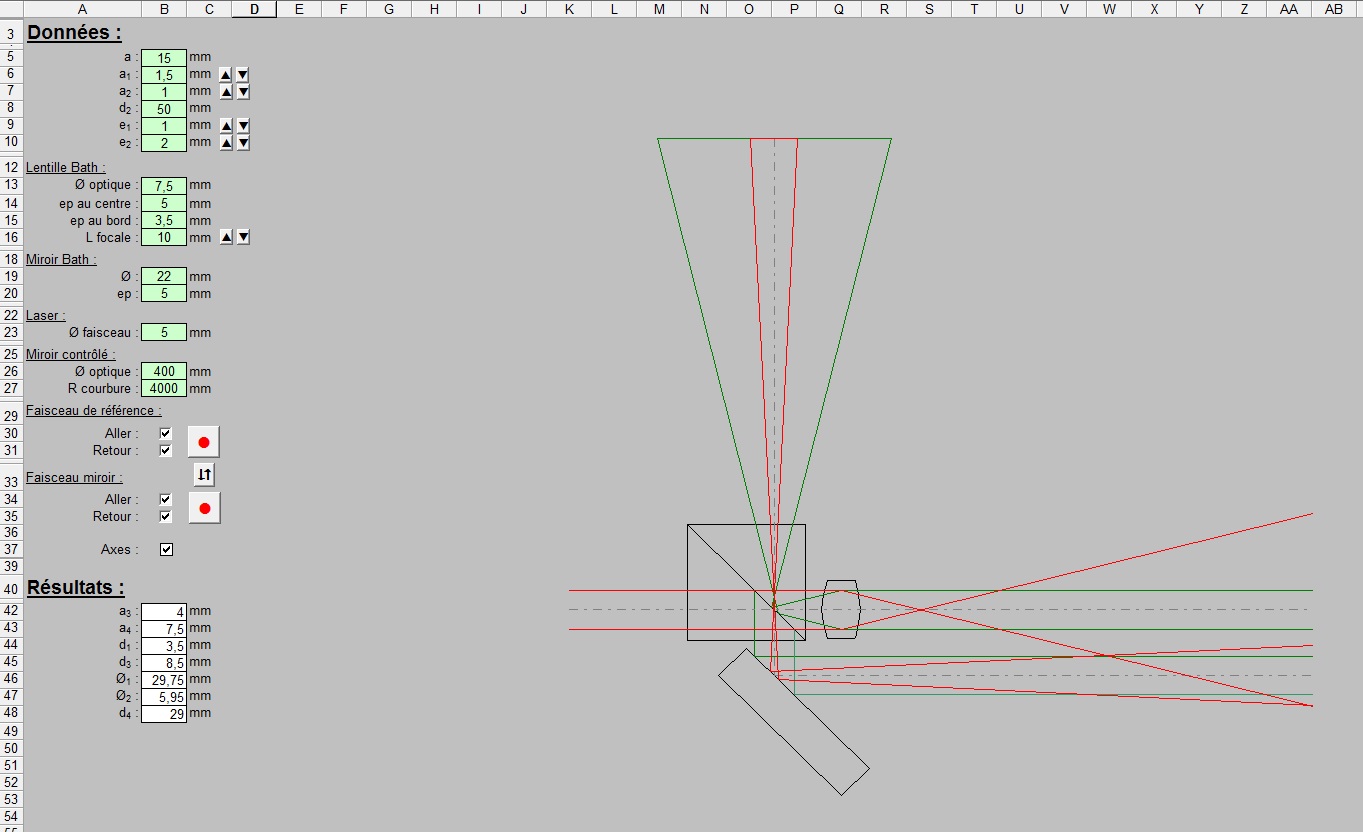Feuille de calcul dimensionnel de l’interféromètre de Bath.Télécharger 
(À utiliser uniquement avec Excel en raison des macros et formats de graphiques spécifiques)

On pourra ainsi :

• Optimiser la distance entre les deux faisceaux parallèles. Une distance inférieure à 8 mm est souhaitable pour limiter l’astigmatisme de montage. Cette exigence peut toutefois être contrainte par les diamètres de la lentille et du faisceau laser.
• Éviter le vignetage sur les faisceaux en dimensionnant et positionnant correctement les pièces optiques
• Mesurer le diamètre des faisceaux au droit de l’imageur et en vérifier la cohérence au regard du matériel utilisé
• Éviter de positionner les foyers sur les faces du cube (sauf celle à 45° car protégée) rendant le front d’onde moins sensible aux défauts (rayures, poussières)

 

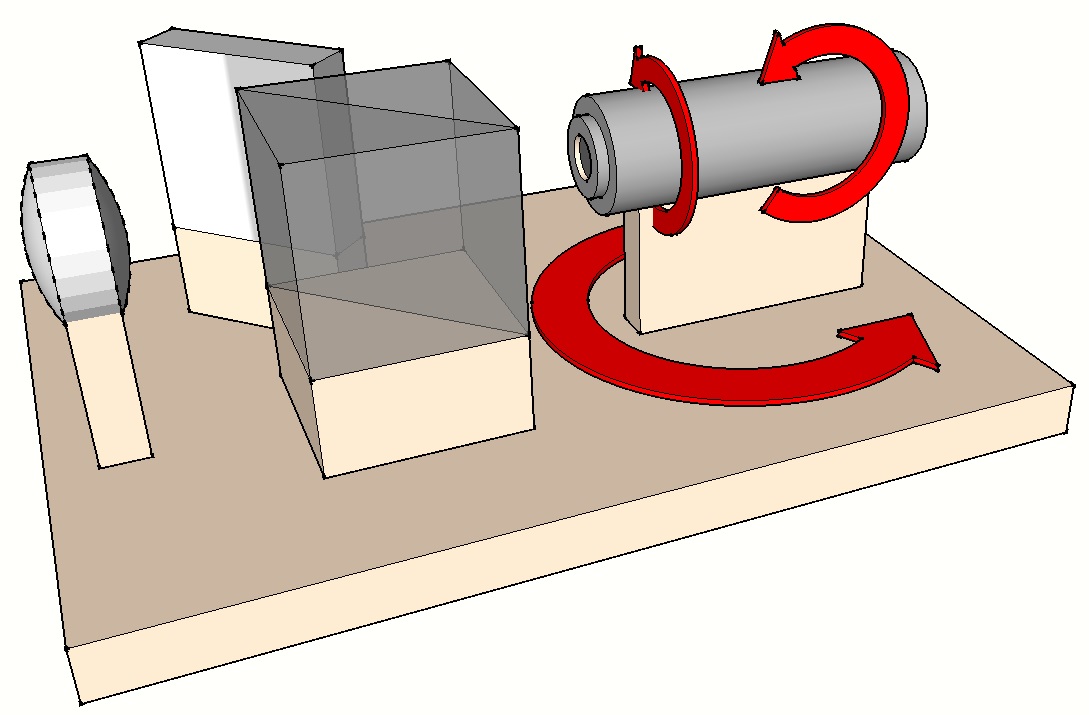
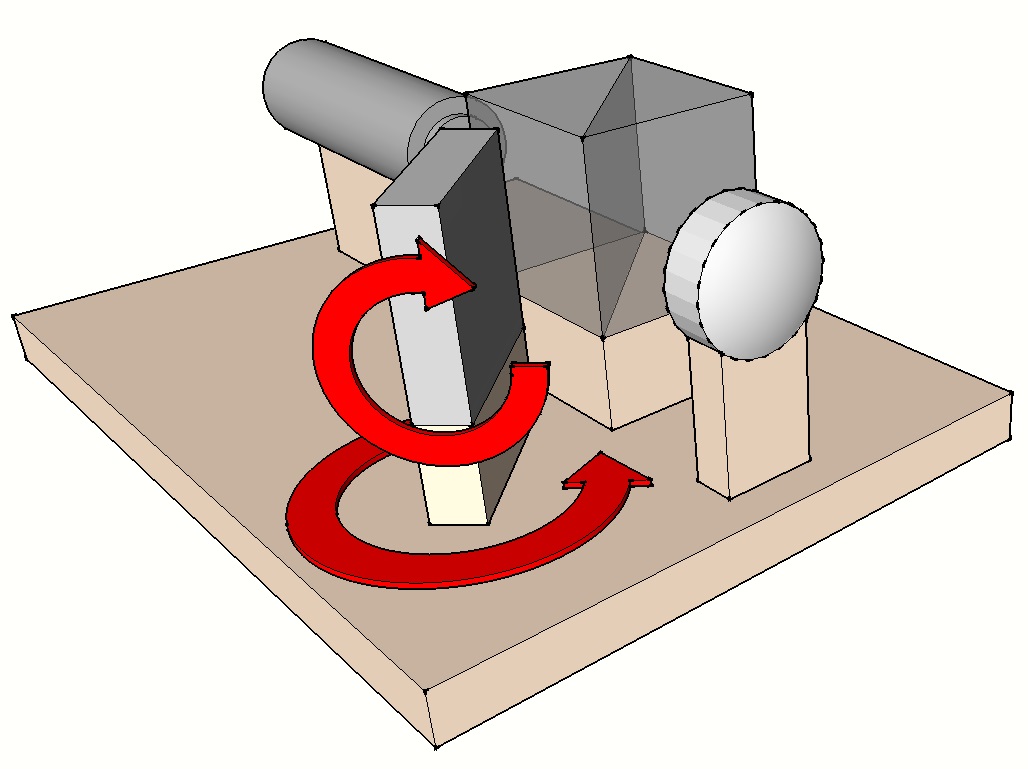
Mouvements de l’interféromètre :

L’obtention d’interférogrammes optimisés pour l’analyse nécessite des réglages fins de la position de l’interféromètre (voir figure ci-dessous) :

• Selon un axe longitudinal (Z) afin de régler le bon focus et obtenir ainsi le nombre de franges adapté.
• Selon deux axes transversaux (X horizontal et Y vertical) afin de régler le tilt et permettre notamment d’obtenir des franges non fermées plus adaptées à l’analyse.

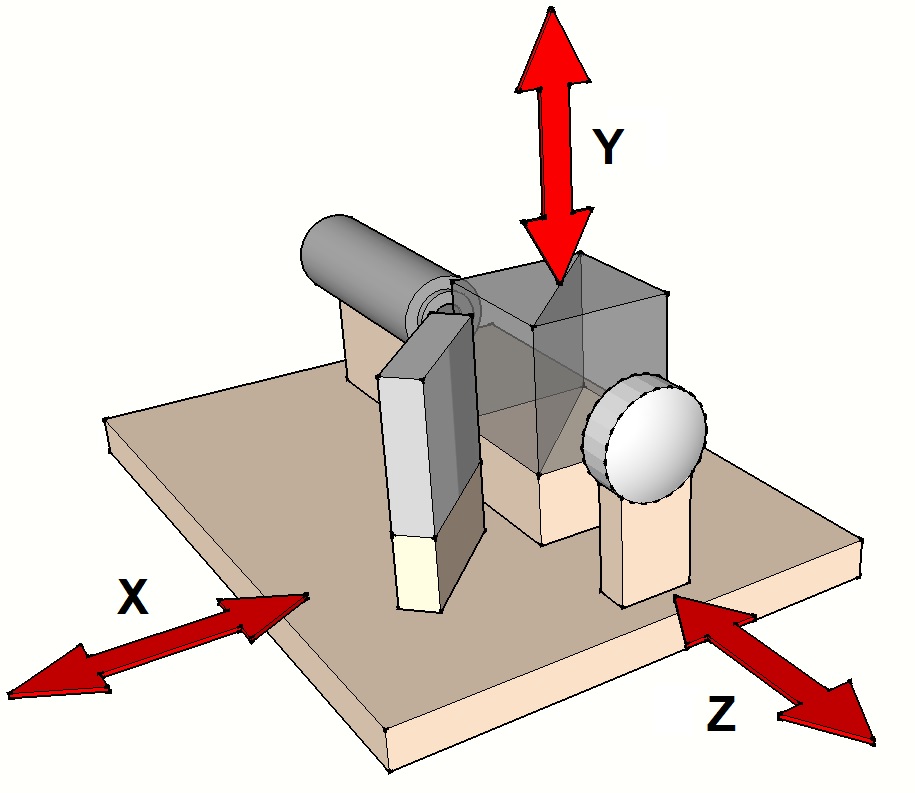
La réalisation pratique de ces mouvements de translation peut s’appuyer sur plusieurs techniques. On peut notamment citer :

• Utilisation de glissières de tiroirs : C’est une solution économique mais suffisamment précise pour ce type d’utilisation. On y adjoindra des vis et ressorts permettant de contrôler les mouvements avec finesse.

• Utilisation d’une table croisée : On en trouve de différents types. On peut par exemple citer des tables utilisées pour des mini-fraiseuses ou des tables micrométriques croisées.

Table croisée PROXXON KT70	Platine micrométrique NEWPORT

Pour réaliser le mouvement en Y (vertical), on peut utiliser un support élévateur de laboratoire.

On peut également motoriser ces mouvements ce qui procure un grand confort d’utilisation (limitation des fibrations, réduction de la turbulence liée à la proximité de l’utilisateur).

Voici quelques exemples de constructions d’interféromètres de Bath par des amateurs aux concepts variés et plus ou moins élaborés :

Source : http://www.dreistein.nl/

Source : http://datscope.wikispaces.com/Bath%20Interferometer

 

Ci-dessous, les interféromètres successifs utilisés au GAP47 :

Pour plus de détails sur la conception de cet interféromètre, cliquez ici.

---

–

 

 

 

Principales causes d’imprécisions :

La méthode de contrôle universelle parfaite n’existe pas. Chacune a ses points forts et ses points faibles. La méthode de Bath n’échappe pas à cette règle. Comme souvent en métrologie, c’est en croisant plusieurs techniques que l’on peut espérer quantifier et qualifier au mieux un objet de mesure. On reconnaît toutefois à la méthode de Bath des avantages indéniables :

• Elle est impersonnelle. La subjectivité de l’opérateur entre peu en ligne de compte contrairement, par exemple, à la méthode de Foucault visuelle pour laquelle l’appréciation des niveaux photométriques des fenêtres est souvent variable d’une personne à l’autre et nécessite une certaine expérience pour obtenir des résultats précis.
• Elle se base sur un échantillonnage important de points de mesure sur la surface contrôlée. En comparaison, la méthode de Foucault se limite à mesurer seulement quelques zones (généralement pas plus d’une dizaine).
• Elle permet de mesurer en une seule fois le front d’onde complet avec ses différents défauts optiques (aberration sphérique, astigmatisme, …). Par contre, avec la méthode de Foucault, il est nécessaire de procéder à des tests spécifiques pour chacun de ces défauts.

Reste la question de la précision de la méthode de Bath. Quelques études ont été effectuées pour comparer ses résultats à ceux de méthodes professionnelles (analyseur de front d’ondes  et interféromètres). On peut par exemple citer les études de :

• Maxwell L. Edwards de l’université d’Aberystwyth : Interféromètre dynamique Twyman-Green sur deux miroirs sphériques D=200 mm
• Stephen C. Koehler : Interféromètre de Fizeau sur miroir parabolique D=310 mm à F/D = 4,1
• Frédéric Jabet (Airylab) dans l’ouvrage « Conception et construction de télescopes et astrographes amateurs » (Editions de boeck) : Inteféromètre Fizeau (Zigo) et analyseur de front d’ondes (HASO) sur miroirs D=113 mm à F/D=4 et D=203mm à F/D=4,5
• Robe Brown et Dale Eason : Inteféromètre Fizeau (Zigo) sur miroir sphérique D=150 mm à F/D = 4

Toutes ces études concluent à une très bonne convergence des résultats obtenus avec l’interféromètre de Bath comparés à ceux des méthodes professionnelles.

Ce constat de fiabilité suppose toutefois que le test soit réalisé dans des conditions optimales afin de limiter au maximum les sources d’erreurs. On peut dresser une liste non exhaustive de ces dernières avec la façon de les minimiser :

 

Aberrations hors axe :

Le principal défaut optique engendré par l’interféromètre de Bath est l’astigmatisme. Il est dû au fait que les faisceaux de test et de référence sont séparés de quelques millimètres. L’image de l’interférogramme se situe donc légèrement hors axe ce qui entraîne inévitablement un astigmatisme de montage. La valeur de ce défaut est donnée par la formule suivante :

Ʃ = D². d² / 16.R³

avec :  D = Diamètre optique du miroir testé
d = Distance de séparation des faisceaux de test et de référence
R = Rayon de courbure paraxial du miroir testé

Le tableau suivant donne quelques valeurs du défaut PTV d’astigmatisme pour différents diamètres et rapports d’ouverture dans le cas d’une séparation de faisceaux de 8 mm :

Diamètre optique	F / D
	3	4	5	6
150 mm	λ / 10	λ / 24	λ / 48	λ / 82
200 mm	λ / 14	λ / 32	λ / 64	λ / 110
300 mm	λ / 21	λ / 49	λ / 95	λ / 165
400 mm	λ / 27	λ / 65	λ / 127	λ / 219
500 mm	λ / 34	λ / 81	λ / 159	λ / 274
600 mm	λ / 41	λ / 98	λ / 191	λ / 329

Comme on peut le constater, la valeur de l’astigmatisme reste souvent négligeable mais peut s’avérer pénalisante pour de petits miroirs à faibles rapports d’ouverture. Heureusement, les principaux logiciels de réduction d’interférogrammes permettent de compenser ce défaut intrinsèque à la méthode. En effet, le logiciel va calculer la valeur de l’astigmatisme à l’aide de la formule ci-dessus et ensuite la retirer du front d’onde brut. Une autre méthode consiste à contrôler le miroir selon plusieurs orientations (typiquement 3 à 5) ce qui permettra au logiciel de détecter l’astigmatisme qui ne tourne pas avec le miroir (celui dont on parle ici) et ainsi de le retirer au moment de la construction du front d’onde.

Enfin, le défaut de coma lié à une analyse hors axe, restera généralement très faible. Celui-ci ne pouvant trouver son origine que dans la configuration de test (et non dans la qualité optique du miroir), il sera volontairement ignoré lors de la construction du front d’onde.

 

Test au centre de courbure :

Faute de pouvoir disposer d’une source située à l’infini, le test s’effectue au centre de courbure ce qui n’est pas sans poser problème (commun d’ailleurs à de nombreuses méthodes de test). Dans ces conditions, le front d’onde émergeant du miroir testé (asphérique) sera donc entaché d’une aberration sphérique lorsqu’il sera comparé au front d’onde de référence. Il faudra en conséquence corriger ou compenser d’une manière ou d’une autre cette aberration de montage pour espérer analyser de façon précise la forme du miroir. Pour ce faire, plusieurs méthodes s’offrent à nous :

• Utiliser une lentille plan convexe entre la source et le miroir afin d’annuler l’aberration sphérique du front d’onde émergeant du miroir testé. Le Dall null test ou le Ross null test décrits par Peter Ceravolo en sont une illustration (Voir chapitre “Ressources”). Les caractéristiques géométriques de la lentille utilisée (diamètre, longueur focale et distance par-rapport à la source) doivent être déterminées en fonction du miroir à tester. Par-ailleurs, la qualité optique de cette lentille doit être particulièrement soignée. Pour toutes ces raisons, cette méthode est relativement peu adaptée à l’amateur.

Configuration du Ross null test (Peter Ceravolo)

• Réaliser le test en auto-collimation. Pour cela, il faut disposer d’un miroir plan de grande qualité optique, percé, aluminé et d’un diamètre au moins égal à celui testé. On place l’interféromètre de Bath au foyer du miroir à contrôler derrière le trou du miroir plan. La source étant située au foyer, les rayons réfléchis par le miroir parabolique seront parallèles entre eux. Suite à leur réflexion sur le miroir plan, ils vont emprunter le même chemin qu’à l’aller pour se focaliser à proximité de la source (l’écart correspond à la distance des deux faisceaux du Bath). En travaillant ainsi au foyer, on élimine toute aberration de sphéricité. Cette solution pourrait apparaître comme idéale si l’on faisait abstraction du coût élevé du miroir plan qui, là aussi, la rend hors de portée de l’amateur.

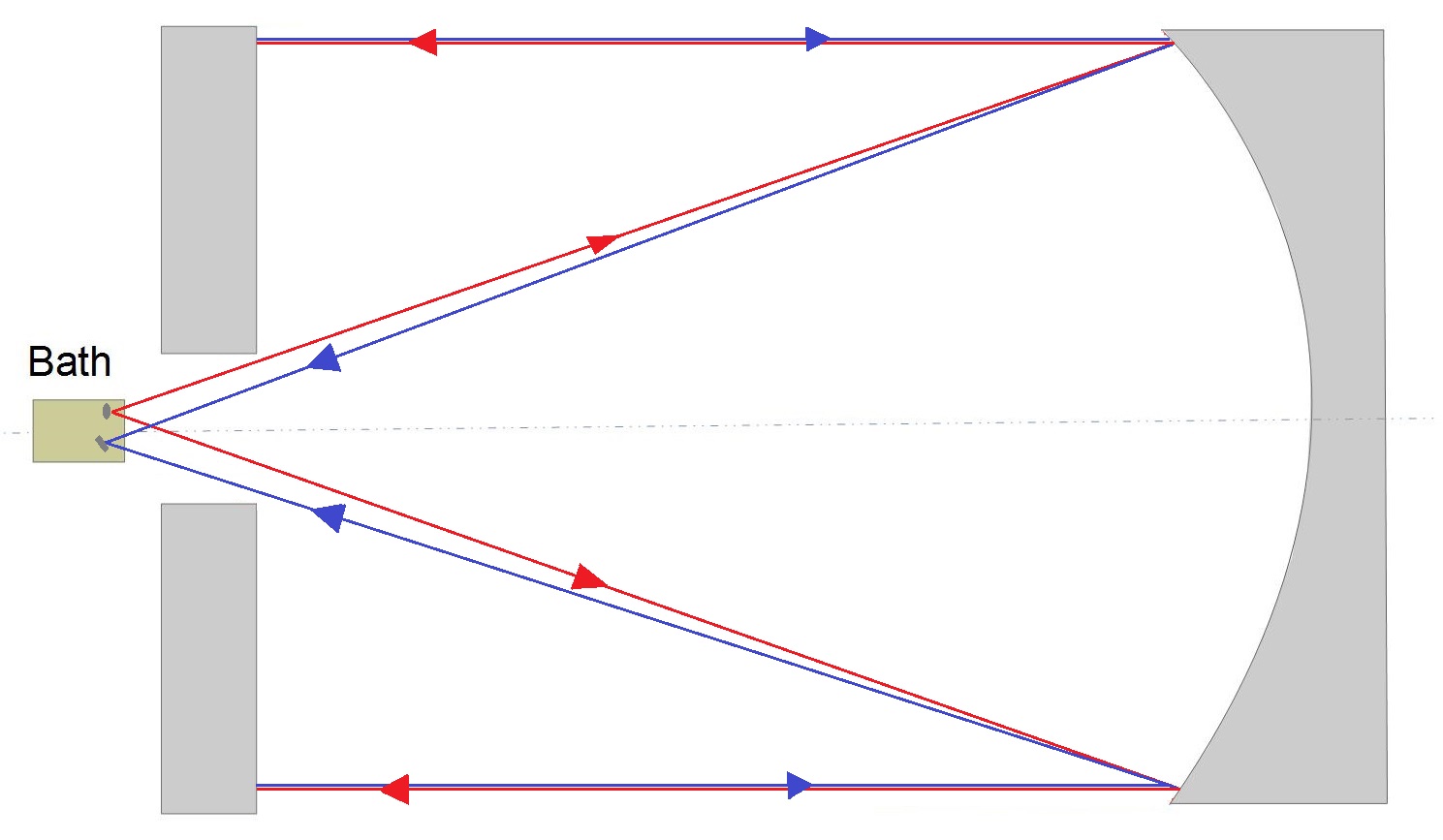Test de Bath en auto-collimation

• Utiliser un null artificiel. La plupart des logiciels de réduction d’interférogrammes disposent d’une fonction de « null artificiel ». Son principe consiste à calculer l’aberration sphérique théorique au centre de courbure puis à la retirer au front d’onde brut. Cette solution est de loin la plus adaptée aux moyens de l’amateur. Elle comporte toutefois des limites qu’il convient d’appréhender :

L’algorithme utilisé par les logiciels pour reconstruire le front d’onde s’appuie sur un développement en série, appelé polynôme de Zernike (pour plus de détails, se reporter au paragraphe « Analyse des interférogrammes »), dont l’un des termes quantifie l’aberration sphérique. Son expression est donnée par la formule :

Z8 = D⁴ / (384 . l . R³).10⁶

avec : D = Diamètre optique du miroir testé (en mm)
l = longueur d’onde de la source laser (en nm)
R = Rayon de courbure paraxial du miroir testé (en mm)
Z8 (Wyant) est exprimé en fraction de longueur d’onde (0 to peak). Il faut donc multiplier cette valeur par 2 pour l’exprimer en PTV (Peak to valley).

 

La précision de ces données aura donc une influence directe sur la valeur exacte de l’aberration de sphéricité et donc du résultat final d’évaluation de la forme du miroir. Le diamètre étant porté à la puissance quatre, il constitue la donnée la plus sensible. La marge d’erreur de sa mesure devra donc être réduite le plus possible. Cette contrainte est d’autant plus délicate à respecter qu’elle concerne deux mesures cumulées : Le diamètre optique du miroir (physique) et de son image dans l’interférogramme lors de son calibrage dans le logiciel.

Le rayon de courbure étant quant à lui porté à la puissance trois, autorisera une plus grande marge d’erreur dans sa mesure.

A titre d’exemple, voici les marges d’erreurs PTV sur le front d’onde causées par une erreur de ±1 mm dans la mesure du diamètre optique :

Rapport d’ouverture	F/D = 3	F/D = 4	F/D =5	F/D = 6
Marge PTV	± λ / 11	± λ / 25	± λ / 49	± λ / 85

Le null artificiel présente enfin un autre inconvénient. La valeur de l’aberration sphérique augmentant (terme Z8), les franges sont de plus en plus déformées et le logiciel de traitement a de plus en plus de mal à les interpréter correctement. Dans la pratique, il semble que les miroirs dont l’aberration sphérique au centre de courbure correspond à une valeur de Z8 supérieure à 10, soient difficiles (voire impossibles) à analyser selon ce procédé.

A titre indicatif, le tableau ci-dessous donne des valeurs de Z8 pour des miroirs de différents diamètres et rapports F/D (calcul à partir de la formule ci-dessus) :

F/D	D optique (mm)
	200	300	400	500	600	800	1000
6	0,5	0,7	0,9	1,2	1,4	1,9	2,4
5	0,8	1,2	1,6	2,1	2,5	3,3	4,1
4	1,6	2,4	3,2	4	4,8	6,4	8
3	3,8	5,7	7,6	9,5	11,4	15,2	19

 

Qualité des composants optiques :

La qualité optique des éléments constituant l’interféromètre de Bath a une importance toute relative. En effet, les deux faisceaux séparés empruntent le même chemin mais dans des sens inverses. Ainsi, les défauts présents sur un dioptre engendreront une déformation du front d’onde qui sera grandement annulée par le même défaut contraire présent dans le front d’onde inverse du faisceau retour. Il faut toutefois rester prudent face à ce postulat théorique car les dioptres sont « attaqués » par les faisceaux aller et retour selon des diamètres de pupilles légèrement différents engendrant ainsi des déformations des fronts d’ondes respectifs plus ou moins variables pour un même défaut de surface d’un élément optique. On veillera donc à éviter les composants de piètre qualité. Des tests ont été effectués par certains praticiens (notamment Dale Eason) utilisant différents composants optiques de qualité courante dans le contrôle d’un même miroir. Ils ont montré une très bonne convergence des résultats confirmant ainsi l’importance relative qu’il convient d’accorder à ce paramètre.

Un traitement antireflets du cube séparateur est souhaitable.

On veillera a ce que les surfaces optiques ne présentent pas de rayures qui pourraient provoquer de la diffusion ou une déformation du front d’onde et nuire ainsi à la qualité des interférogrammes.

Enfin, on s’attachera à la qualité optique de l’objectif photographique utilisé. De manière générale, on préférera un objectif à focale fixe mieux optimisé qu’un zoom. Le principal défaut de l’objectif nuisible à la qualité des interférogrammes est la distorsion. Il est toutefois possible de retirer artificiellement ce défaut par voie logicielle (voir paragraphe « Mise en œuvre du test »). On pourra également se reporter à des tests d’objectifs édités sur le Net afin de choisir l’équipement le mieux adapté (voir chapitres « Ressources »).

 

Précision des alignements optiques :

La fiabilité du test nécessite quelques réglages d’alignements optiques qui conditionnent le résultat final et sur lesquels il convient de porter une attention particulière :

• Parallélisme des faisceaux : Celui-ci devra être ajusté au mieux faute de quoi un défaut d’astigmatisme est susceptible de fausser les résultats.
• Éviter le vignetage : Les faisceaux ne doivent pas être partiellement interrompus par des obstacles ou des ouvertures insuffisantes d’éléments optiques. On s’aidera d’une épure pour s’assurer qu’il n’en est rien (voir le paragraphe « Positionnement des composants » ci-dessus). Le vignetage peut également être introduit par le diaphragme de l’appareil photo si son ouverture est trop faible ou si l’objectif est trop éloigné du cube séparateur.
• Centrer et orienter la lentille : On fera en sorte de centrer au mieux les faisceaux aller et retour sur la lentille. Son orientation devra également faire en sorte que l’ouverture du faisceau couvre entièrement le miroir afin d’obtenir un éclairage uniforme et éviter ainsi des pertes de contraste sur une partie d’interférogramme. Un défaut d’orientation peut également induire un astigmatisme par ovalisation de la figure.

Le paragraphe « Mise en œuvre du test » ci-après décrit les méthodes pour optimiser ces réglages.

Exemple d’un effet du au vignettage

Exemple d’éclairage non uniforme

Qualité des interférogrammes :

L’algorithme de modélisation du front d’onde utilisé par le logiciel de traitement des résultats doit disposer d’interférogrammes dépourvus autant que possible de défauts afin de limiter les biais dans l’analyse de la précision de la forme testée. On peut passer en revue quelques défauts d’interférogrammes parmi les plus courants :

 

Reflets parasites :

Ils sont dus en général à des réflexions indésirables sur les faces optiques des composants de l’interféromètre. Le plus couramment rencontré est causé par une double réflexion interne au cube séparateur qui produit deux spots lumineux sur les images. On pourra placer un écran opaque entre l’interféromètre et le miroir testé pour constater que les spots seront toujours présents révélant ainsi l’origine interne au cube du phénomène. La présence de ces reflets sur la partie utile de l’interférogramme nuira inévitablement à l’analyse. Pour s’en affranchir, il convient d’opérer une légère rotation du cube séparateur jusqu’à rejeter les spots en dehors du périmètre de l’interférogramme.

Une surface optique testée mal nettoyée peut également engendrer des reflets parasites. En effet, le faisceau laser de référence rencontrant cette surface diffusante va produire un reflet nuisible. La surface optique du miroir testé devra donc être parfaitement nettoyée en prévision du contrôle.

Double spot (reflet interne au cube)

Reflet diffusant du faisceau de référence (au centre)

Artefacts :

Des artefacts peuvent également biaiser l’analyse des franges.

On constate souvent la présence de sortes de bulles sur les images d’interférogrammes. Elles sont principalement dues à des poussières déposées sur les surfaces optiques des composants de l’interféromètre mais également sur l’objectif photographique. Pour limiter ce phénomène, il conviendra de procéder à un dépoussiérage à la poire soufflante ou à l’aide d’un tissus approprié (type Pec Pap par exemple). En période d’inutilisation, l’interféromètre devra être stocké dans une enceinte hermétique à la poussière.

Par-ailleurs, les interférogrammes peuvent présenter un aspect spongieux généralement causé par des lentilles de modules laser en plastique. Le manque d’homogénéité de ce matériau est en effet souvent à l’origine de ce phénomène. Pour y remédier, on s’orientera donc vers des optiques en verre.

De plus, sur les modélisations de fronts d’ondes, on voit parfois s’incruster le spectre des franges de l’interférogramme à partir duquel elles ont été construites. En anglais, cet artefact porte le nom de « print through » qu’on pourrait traduire littéralement par « imprimé à travers », expression qui reflète bien la nature du phénomène. Il s’agit en fait d’un biais de calcul lié essentiellement à la non linéarité photométrique de l’interférogramme. La principale cause est en général à rechercher dans la correction gamma interne à l’appareil photo ou, plus rarement, à un logiciel de traitement d’images. Ce défaut peut également se produire en cas de saturation d’une partie des franges. L’idéal consiste d’abord à déconnecter la correction gamma automatique de l’imageur si cela est possible. A défaut, on pourra sensiblement atténuer les effets indésirables de ce phénomène en limitant l’intensité lumineuse des franges à environ la moitié de l’échelle des niveaux de gris. Dans ces conditions, la correction gamma automatique sera limitée et, de fait, le défaut de « print through » également. On pourra enfin lisser les résidus de ce défaut en moyennant les fronts d’ondes de plusieurs interférogrammes dont l’orientation des franges aura été modifiée pour chacun d’eux (voir paragraphe « Mise en œuvre du test »).

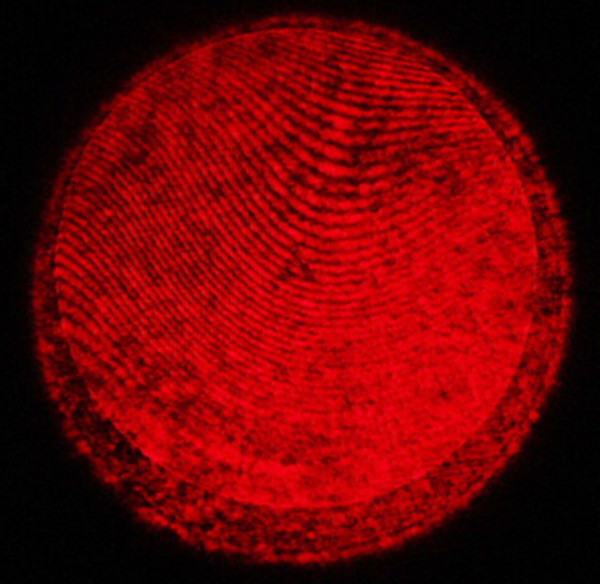Présence de bulles	Aspect spongieux

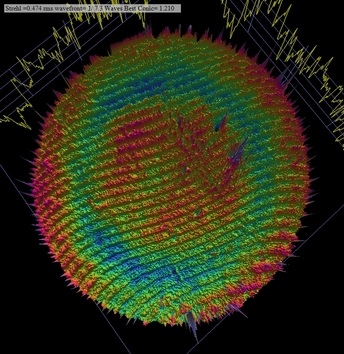Défaut de « print through » sur un front d’onde

Notons enfin qu’il conviendra d’éviter tout masque dans le périmètre d’un interférogramme (par exemple une patte de maintien du miroir) qui perturbera localement l’analyse du front d’onde. On verra toutefois qu’il est possible de neutraliser ces zones au besoin lors de la modélisation.

 

Manque de contraste ou de définition des franges :

En tout premier lieu, comme signalé précédemment, il convient d’éclairer uniformément le miroir testé en positionnant correctement la lentille convergente de l’interféromètre. On obtiendra ainsi un contraste homogène des franges sur toute la surface de l’interférogramme.

Le nombre de franges influe également sur leur contraste. Des franges trop nombreuses, et donc trop resserrées, produisent des interférogrammes diffus plus difficilement exploitables pour l’analyse par le logiciel de modélisation du front d’onde. A l’inverse, plus faible sera l’échantillonnage des franges, moins grande sera la précision du calcul de la forme. Il convient donc de trouver un compromis entre ces deux exigences : un échantillonnage de 30 à 50 franges pour un interférogramme semble satisfaisant à l’usage. Avec des miroirs ouverts (F/D=4 ou moins) on aura tendance à obtenir un maximum de franges pour éviter que certaines ne soient circulaires.

Par ailleurs, la mise au point devra être soignée afin d’optimiser le contraste des franges. Elle s’effectue sur le miroir (donc à une distance correspondant au rayon de courbure) et non à l’infini.

Un autre phénomène influe sur le contraste du réseau de franges : la polarisation des faisceaux laser à travers le cube séparateur qui peut avoir pour conséquence d’en déséquilibrer l’intensité lumineuse. Le meilleur contraste sera obtenu lorsque les faisceaux auront une luminosité équivalente. On fera varier l’intensité respective des flux lumineux en ajustant l’orientation du module laser selon son axe jusqu’à obtenir le meilleur contraste. Le paragraphe « Mise en œuvre du test » ci-après donne à l’utilisateur les moyens d’y parvenir. On pourra également placer un filtre polarisant linéaire rotatif devant la source laser. Celui-ci renforcera le contraste des franges et contribuera à « nettoyer » les interférogrammes du bruit de fond et autres artefacts.

Enfin, la résolution des interférogrammes ne doit pas être trop faible afin que l’algorithme soit en mesure d’interpréter correctement le tracé des franges. En fonction de la taille de la matrice et des photosites  de l’imageur, on choisira une focale d’objectif capable de restituer une largeur de frange supérieure à cinq pixels. On veillera également à sélectionner un format d’image dont le niveau de compression devra être limité de ce point de vue.

 

Conditions de test :

 De manière plus classique, les sources d’erreurs peuvent provenir du contexte associé au contrôle ainsi qu’à son mode opératoire. Parmi les paramètres pouvant influer sur les résultats, on peut principalement citer :

 

Stabilité de l’air :

Comme d’autres tests optiques, l’interférométrie est sensible aux turbulences de l’air ambiant qui peuvent déformer les fronts d’ondes et fausser ainsi les résultats. Pour limiter ce phénomène, on réalisera les contrôles dans un local thermiquement stable et préservé des courants d’air. Pour améliorer encore les conditions du test, on peut réaliser un tunnel. L’utilisation du tissu est particulièrement adaptée car celui-ci bloque les mouvements d’air tout en limitant les gradients de température pouvant générer des mouvements de convection (voir exemple ci-dessous). Enfin, on limitera au maximum la présence de personnes dans l’environnement proche du banc de contrôle afin de ne pas générer de turbulence.

Vibrations :

En théorie, les faisceaux de l’interféromètre de Bath utilisant un chemin commun, le dispositif devrait être moins sensible aux vibrations que d’autres (test de Foucault par exemple). La pratique montre toutefois que ce postulat est loin d’être vérifié et qu’il convient donc de prendre certaines précautions afin de limiter les effets induits  de ce phénomène. On s’éloignera si possible de toute source de vibrations (trafic routier, personnes à proximité, …). On privilégiera un local dont la structure sera stable et à forte inertie (notamment le plancher). Concernant le banc optique lui-même, on aura intérêt à rigidifier l’ensemble en solidarisant par exemple le miroir sous test de l’interféromètre par l’intermédiaire de poutres.

Les vibrations différentielles seront ainsi largement atténuées. Les vibrations peuvent par-ailleurs être générées par le déclenchement de l’obturateur de l’appareil photo. Pour y remédier, on dotera ce dernier d’un support rigide à forte inertie. On pourra également solidariser les supports de l’appareil photo et de l’interféromètre.

Enfin, en s’efforcera de limiter les interventions manuelles lors des phases de prises de vues. Des commandes motorisées de mouvements de l’interféromètre et des déports de réglages de l’appareil photo peuvent utilement répondre à cet objectif.

Exemple de commandes déportées des mouvements xyz (pupitre) et des prises de vue

Supportage du miroir :

Généralement, le contrôle s’effectue miroir en position verticale ou légèrement inclinée. En présence d’une grande pièce optique, notamment de faible épaisseur, on est plus ou moins confronté à des contraintes mécaniques et à des risques de pliure du disque sous son propre poids générant en particulier de l’astigmatisme qu’il sera difficile de dissocier des défauts propres au miroir. On peut toutefois tenter de limiter ce phénomène au travers de diverses solutions :

 

• Support incliné :

Dans le cas d’un contrôle en position légèrement inclinée, on peut envisager de placer le miroir dans son barillet définitif ou en fabriquer un spécifiquement pour les contrôles. Dans cette configuration, les forces résultantes reportées sur le dos seront faibles et le nombre d’appuis pourra ainsi être limité. Par contre, il conviendra d’apporter une attention particulière aux appuis latéraux qui reprendront l’essentiel des efforts. La solution de quatre points d’appui avec roulements sur deux balanciers est considérée comme parmi les plus performantes (voir exemple ci-dessous).

 

• Support vertical :

Cette solution est privilégiée par certains professionnels. Le miroir verticalisé repose sur la tranche par l’intermédiaire d’appuis durs constitués de deux rondelle en Nylon assez peu épaisses (voir exemple ci-dessous). Ces deux contacts seront placés dans le plan du centre de gravité du miroir, ce dernier se trouvant ainsi en équilibre. Des pattes éviteront un basculement accidentel. On peut espérer ainsi une compensation des contraintes à l’origine d’un astigmatisme de pliure. Le poids important reporté sur seulement deux points d’appui occasionne un  poinçonnement pouvant générer un défaut de trefoil.

Source : Joerg Peters

• Installation rapide :

Cette méthode consiste à laisser reposer le miroir quelques heures afin qu’il libère les contraintes. Pour cela, on peut le déposer à plat sur un molleton relativement souple et homogène ou sur son barillet. On l’installera ensuite sur le support de contrôle et on effectuera les tests sans délai avant qu’il ne commence à plier significativement sous son poids. Les manipulations s’effectueront avec des gants isolants afin d’éviter des contraintes thermiques dans le disque de verre.

• Support horizontal :

Dans l’idéal, il serait préférable de réaliser les contrôles miroir horizontal installé dans son barillet définitif. On évacuerait ainsi le délicat problème des appuis latéraux. Quant au maintien du dos, il serait parfaitement géré par des appuis adaptés. En revanche, ce mode opératoire nécessite une hauteur utile disponible équivalente au rayon de courbure du miroir testé. Il faut pour cela disposer d’une fosse (un puits par exemple) ou d’un local avec une hauteur sous plafond en conséquence. Cette contrainte est souvent rédhibitoire. Autre difficulté liée à ce mode opératoire : la stratification des couches d’air (gradient de tampérature) dont il conviendra de maîtriser les effets. Si ce procédé devait toutefois être mis en œuvre, il convient d’utiliser un miroir plan pour couder le faisceau et installer l’appareil de contrôle en position horizontale à l’écart de l’enveloppe verticale du miroir contrôlé. On y gagnera ainsi en termes d’ergonomie et on se préservera des risques de chute d’objets sur la surface optique.

 

On peut lever quelques doutes sur la présence d’un astigmatisme de pliure susceptible de parasiter les résultats au travers de deux méthodes :

• On peut réaliser plusieurs contrôles successifs du miroir selon des orientations différentes. Pour chacune d’elles, on évalue l’amplitude et l’orientation d’un éventuel défaut d’astigmatisme à l’aide d’un interféromètre ou d’un appareil de Foucault équipé d’une étoile artificielle. Si le défaut tourne exactement comme le miroir, il peut être imputé à une forme optique imparfaite. S’il garde une orientation stable, on peut légitimement diagnostiquer un astigmatisme de pliure. De plus, si l’amplitude du défaut reste également constante, on peut considérer que seul ce dernier défaut est présent et qu’il peut donc être ignoré. A défaut, un résidu d’astigmatisme intrinsèque à l’optique est à prendre en considération. Ce postulat suppose toutefois que les effets de pliure soient reproductibles pour chaque orientation du miroir ce qui impose une certaine prudence s’agissant de grands miroirs minces. Certains logiciels d’analyse d’interférogrammes intègrent des fonctions de mise en évidence de l’astigmatisme de pliure et permettent de le retirer du front d’onde brut.
• On peut également installer le miroir dans son tube de destination équipé d’un barillet de qualité. On réalise alors un startest sur une étoile proche du zénith afin que le miroir repose bien sur son dos sans solliciter les appuis latéraux. Dans le cas d’un miroir non aluminé, on choisira une étoile très brillante. Si les plages intra-focale et extra-focale restent parfaitement circulaires, on pourra considérer que le miroir est exempt de défaut d’astigmatisme. Les défauts constatés sur le banc de contrôle pourront donc être imputés à une pliure du miroir. A l’inverse, en cas d’ovalisation des figures tournant de 90° entre les positions intra et extra, il conviendra d’estimer l’amplitude de l’astigmatisme et de repérer son orientation. Par précaution, on fera tourner le miroir dans son barillet pour vérifier que le défaut d’astigmatisme observé à l’oculaire tourne également et qu’il est donc imputable à l’optique.

 

Moyenner des mesures :

On rappellera un principe essentiel en métrologie : On augmente la précision des mesures en multipliant leur nombre. On aura donc intérêt à appliquer ce mode opératoire aux mesures interférométriques en procédant de la façon suivante :

• Pour une orientation de miroir donnée, on réalisera plusieurs interférogrammes en variant les inclinaisons et le nombre de franges. Pour ce faire, on déplacera légèrement l’interféromètre en tilt et en focus (mouvements xyz).
• On renouvellera ces prises de vues pour plusieurs orientations du miroir qu’on aura pris soin de repérer précisément.

Au terme de chacune de ces phases, on réalisera une moyenne des résultats. Les fronts d’onde  obtenus gagneront ainsi en informations utiles alors que les phénomènes aléatoires et indésirables seront grandement atténués (bruit de fond, artefacts, effets liés à la turbulence, pliure du miroir, …).

Le nombre de mesures peut être considéré comme suffisant quand le fait d’en rajouter n’influe plus significativement sur les résultats.

---

–

 

 

 

Mise en œuvre du test :

 

Réglages et prises de vues :

On peut décomposer le protocole de mesures en étapes successives :

• Nettoyer le miroir pour limiter la diffusion de sa surface optique et éviter les reflets indésirables.
• Dépoussiérer (voire nettoyer si nécessaire) les surfaces optiques des composants de l’interféromètre et de l’appareil photographique. On pourra utiliser une poire soufflante, un pinceau à poils doux ou des tissus spéciaux de nettoyage d’optiques (type Pec Pad).

Dépoussiérage des composants optiques à la poire

• Marquer des repères d’orientation du miroir sur sa tranche. On tracera des traits sur la tranche au feutre indélébile séparés de 45° par exemple avec inscription de l’angle par ordre croissant dans le sens inverse des aiguilles d’une montre (certains praticiens ont obtenu de meilleurs résultats avec 5 orientations séparées de 72°). Une certaine précision étant requise, on pourra s’aider d’un ruban de papier épais entourant le miroir qu’on marquera d’autant d’intervalles souhaités une fois déployé sur une table. Un repère de référence sera placé sur le support de test.
• Mesurer avec précision le diamètre optique du miroir (à 5/10 mm près si possible). Une règle plastique graduée de précision est bien adaptée à cet usage.
• Installer le miroir sur son support de contrôle. Utiliser des gants propres, isolants et antidérapants. Un délai approprié devra être respecté avant de procéder aux mesures afin de permettre un éventuel équilibrage thermique ou mécanique. Pendant ce laps de temps, la surface optique sera protégée des poussières.
• Mesurer avec précision le rayon de courbure paraxial du miroir (rayon de courbure de la zone centrale). Pour ce faire, on pourra utiliser un mètre à ruban de qualité ou un télémètre de précision à partir d’une coupe à l’appareil de Foucault.
• Si le module laser dispose d’une lentille focusable, régler celle-ci le cas échéant afin d’obtenir un faisceau à rayons parallèles. Pour le vérifier, on déplacera un écran sur le chemin du faisceau en vérifiant que le diamètre du spot reste constant sur plusieurs mètres.
• Installer l’interféromètre dans sa configuration de contrôle. Le plan de la lentille de celui-ci sera placé à une distance correspondant au rayon de courbure paraxial du miroir testé.

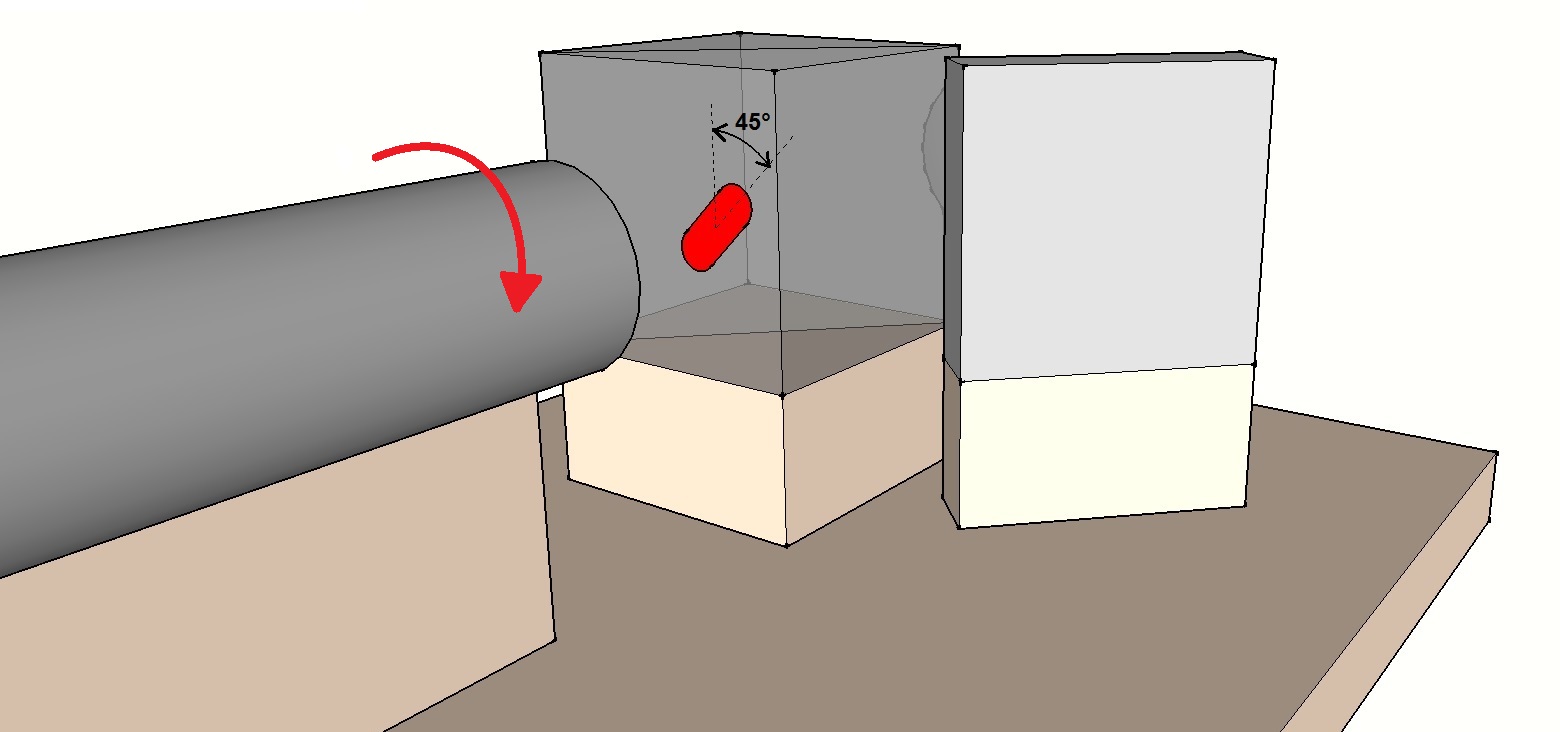
• Régler sommairement le parallélisme du faisceau laser avec l’axe de déplacement en Z du support de l’interféromètre. Ce prérequis offrira un confort lors des derniers ajustements en faisant en sorte que les déplacements en focus (Z) n’introduisent pas du tilt (X et Y). Pour effectuer ce réglage, on projette le spot laser sur un écran situé au niveau du support du miroir et on observe son éventuelle dérive lors des déplacements en Z de l’interféromètre. Au besoin, ajuster l’orientation du module laser ou de l’interféromètre jusqu’à obtenir l’immobilité du spot.
• Tourner le laser sur son axe afin d’obtenir le meilleur contraste des franges en raison de la polarisation du faisceau dans le cube séparateur. Dans le cas d’un laser rouge, le spot a une forme rectangulaire qui permet de situer son orientation. L’expérience montre qu’une inclinaison à 45° permet d’équilibrer l’intensité lumineuse des faisceaux laser en sortie de cube garantissant un contraste optimum des franges. Les lasers verts, quant à eux, génèrent des spots circulaires. La rotation optimale du module laser devra donc être réalisée expérimentalement par appréciation itérative des contrastes de franges d’une série d’images d’interférogrammes.

• Retirer ou déplacer la lentille pour vérifier le parallélisme des faisceaux émergeant de l’interféromètre. On peut s’aider pour cela d’un écran sur lequel on trace des repères et que l’on déplace en s’éloignant de l’interféromètre (voir photo ci-dessous). La distance entre les deux spots doit rester constante. A défaut, on agira sur l’orientation du petit miroir plan jusqu’à ce que les faisceaux soient parallèles.

• Replacer la lentille et s’assurer que le faisceau laser est bien centré dessus. A défaut, ajuster le positionnement de la lentille par des translations (voir figures ci-dessous).

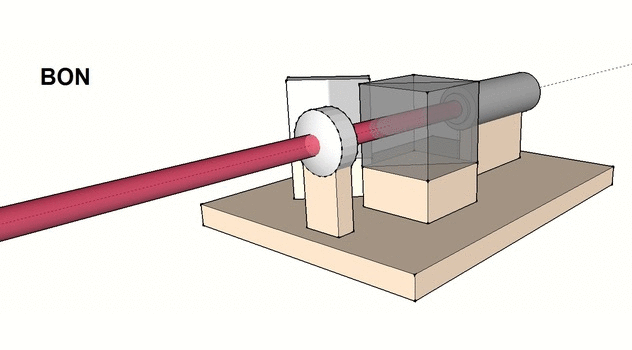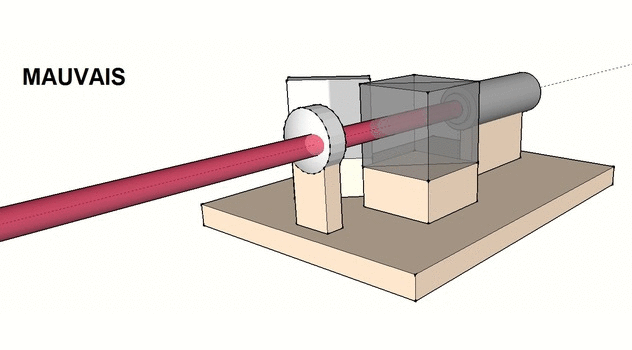
• Ajuster l’orientation de la lentille de telle sorte que le faisceau émergeant couvre la totalité du miroir (voir figures ci-dessous).

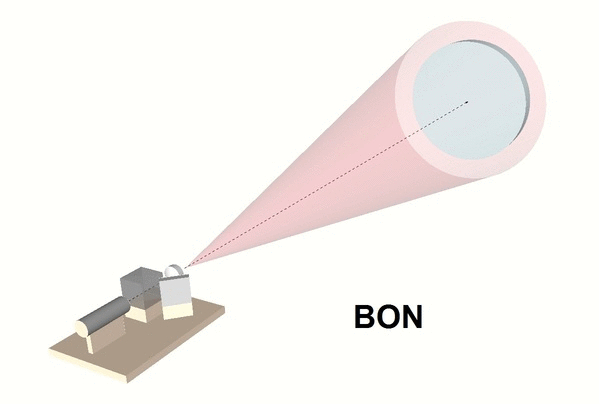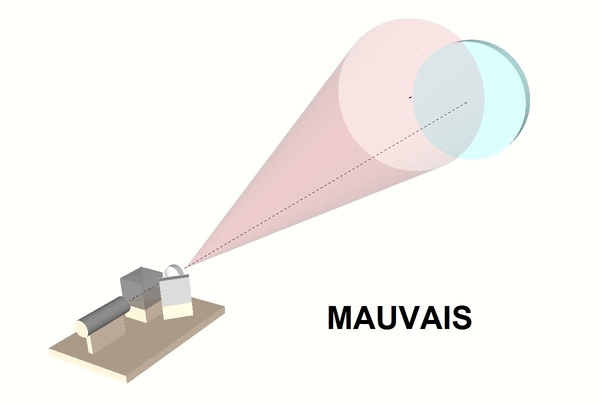
Pour faciliter ce réglage, on va réaliser un écran (voir figure et photos ci-dessous). On trace d’abord deux croix matérialisant les axes des deux faisceaux émergeant de l’interféromètre et séparées de la distance d correspondant à la séparation des faisceaux. On matérialise ensuite des cercles concentriques centrés sur la première croix. On place l’écran face à l’interféromètre et on le déplace d’avant en arrière. Le spot (faisceau de référence) est positionné sur la deuxième croix. Le faisceau émergeant de la lentille (rectangulaire pour un laser rouge, circulaire pour un laser vert) doit quant à lui rester centré sur les cercles concentriques lorsque l’on translate l’écran. Si ce n’est pas le cas, on ajustera les orientations de la lentille jusqu’à ce que le centrage soit satisfaisant.

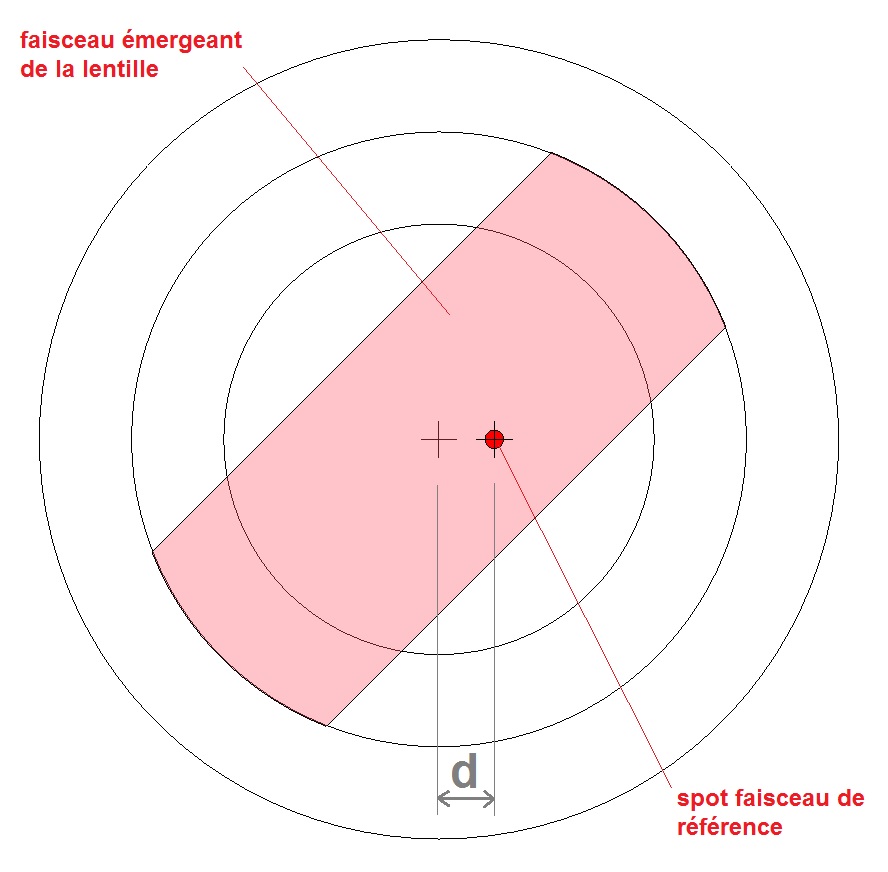• Orienter l’interféromètre de telle manière que le spot du faisceau de référence se situe vers le centre du miroir testé. La précision de ce centrage n’est pas critique. D’ailleurs pour les miroirs troués (type Cassegrain par exemple), on doit par obligation s’écarter du centre et viser le bord du trou. Il convient toutefois de ne pas trop s’éloigner du centre au risque de générer un astigmatisme de montage.
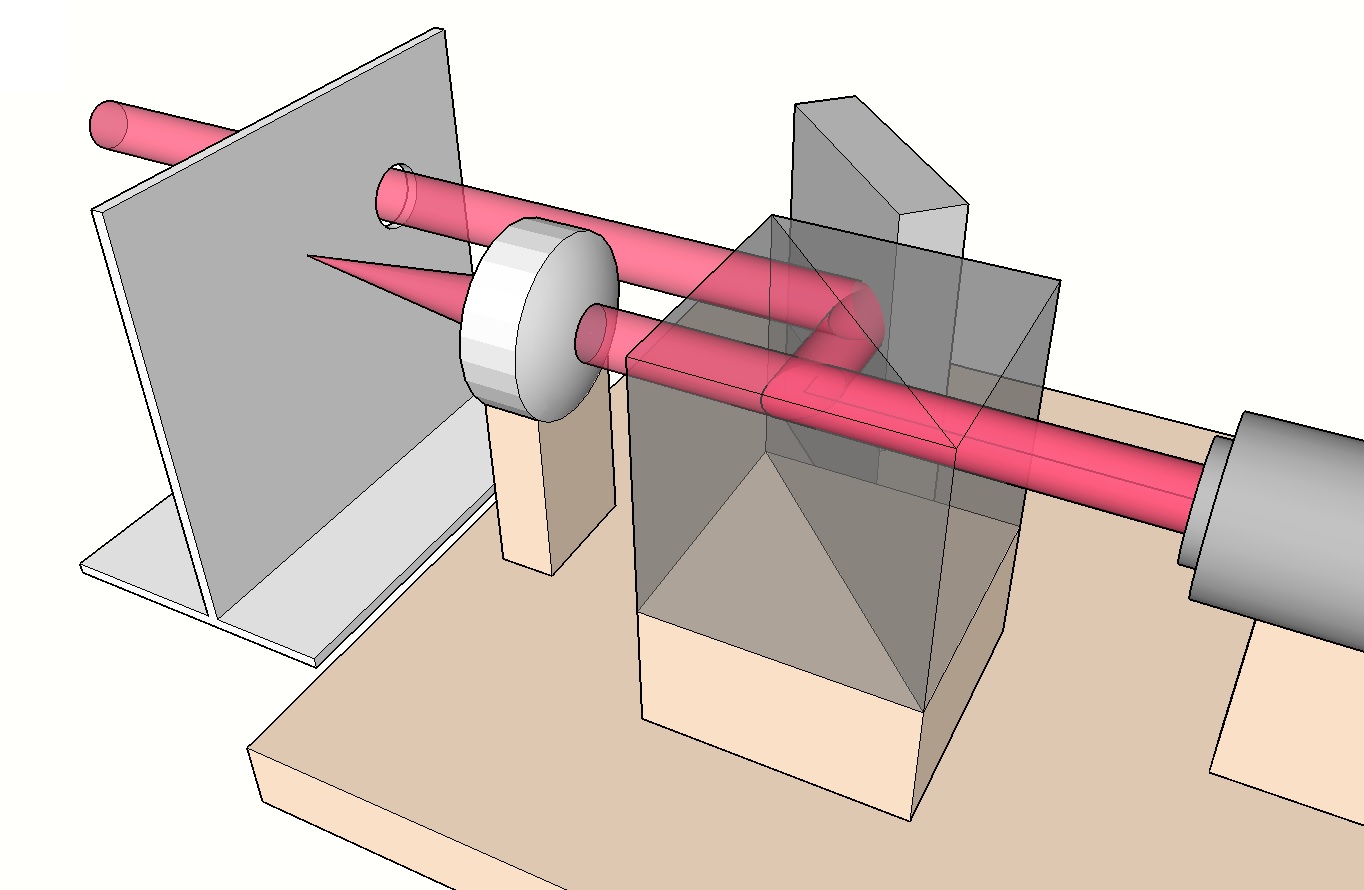
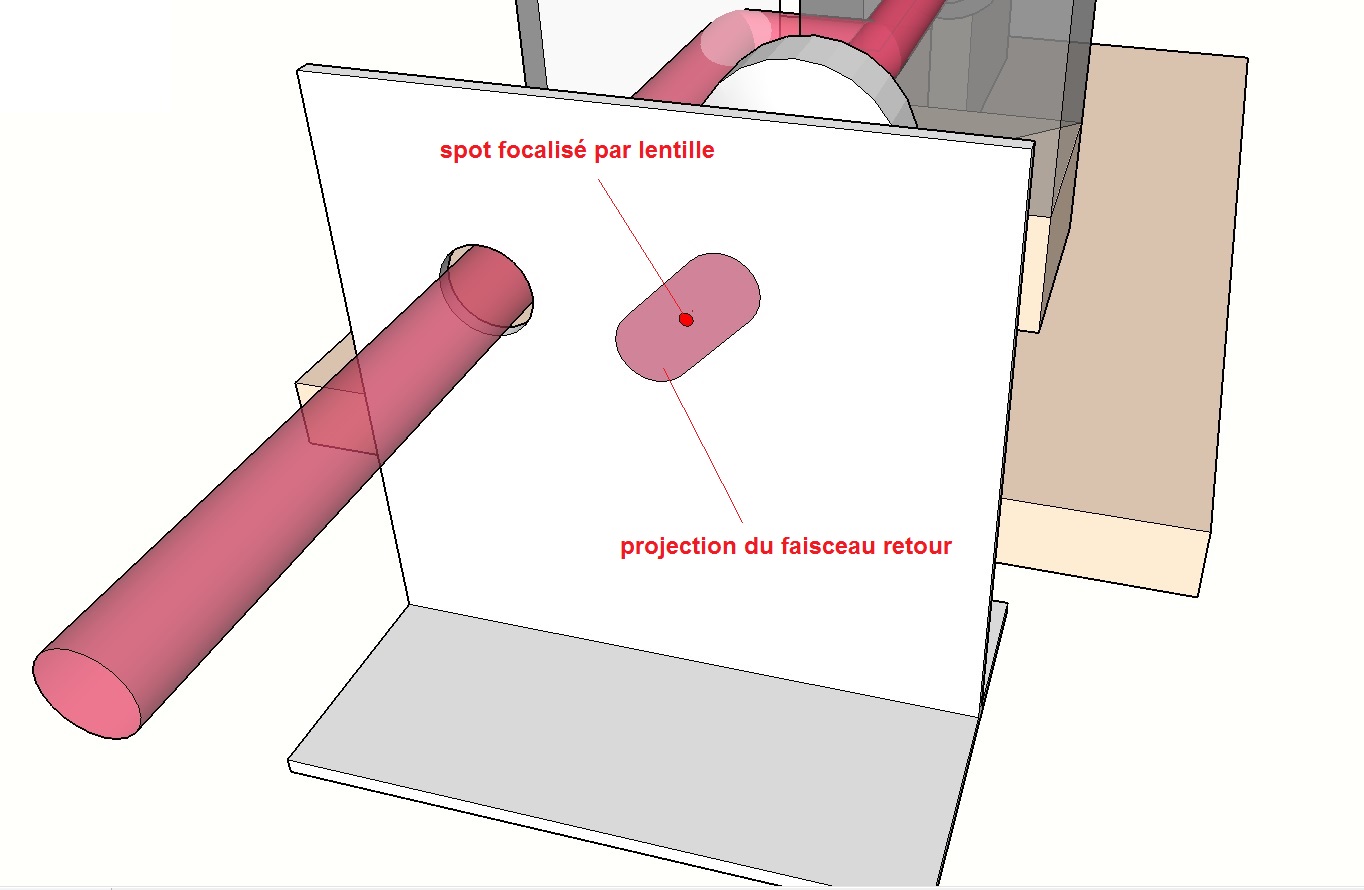
• Chercher le retour du faisceau de référence réfléchi par le miroir testé au voisinage de l’interféromètre. On pourra s’aider pour cela d’un écran blanc que l’on déplace dans l’environnement de l’interféromètre. La manipulation consiste à diriger ce faisceau au centre de la lentille. On pourra dans un premier temps agir grossièrement sur l’orientation du miroir testé (sans trop décentrer le spot) afin d’approcher la position. Pour affiner le réglage, on utilisera un petit écran en bristol que l’on positionnera approximativement dans le plan focal de la lentille (voir figures ci-dessous). Celui-ci laissera passer le faisceau de référence émergeant du miroir plan à travers un trou pour le laisser librement se diriger vers le miroir testé. Le faisceau émergeant de la lentille se focalisera quant à lui sur l’écran en bristol. Le petit spot qu’il formera sera visible par transparence sur l’autre face de l’écran en bristol. Le retour du faisceau de référence, quant à lui, se projettera sur l’écran après réflexion sur le miroir testé. La marque qu’il formera aura la section du faisceau (de forme rectangulaire pour un laser rouge, ronde pour un laser vert). La finalisation du réglage va donc consister à centrer le petit spot focalisé dans le grand. Pour ce faire, on agira sur les mouvements fins en x et y du support de l’interféromètre.

Afin de faciliter les opérations, on peut faire apparaître et disparaître la tache retour par des mouvements de main occultant le faisceau de référence. On visualisera ainsi mieux la précision de centrage des deux spots.

• Positionner un écran en sortie de cube séparateur et à une distance de 20 à 30 cm. Pour plus de confort, on peut également procéder par transparence derrière un calque peu opaque. On doit normalement distinguer deux disques lumineux :

– Un grand disque pâle : Il est créé par le faisceau de référence émergeant de la lentille de l’interféromètre. Dans le cas d’un laser rouge sa forme sera plus proche du rectangle.
– Un plus petit disque brillant : Il est créé par le faisceau de référence émergeant du miroir contrôlé.

En ajustant finement le tilt (mouvements en x et y) , il faut faire en sorte que ces deux disques se chevauchent en totalité et de préférence en les centrant au mieux pour faire apparaître des franges (à cette échelle, elles ne sont pas toujours facilement distinguables). Avec l’habitude, cette étape pourra être évitée et directement réalisée via l’appareil photo.

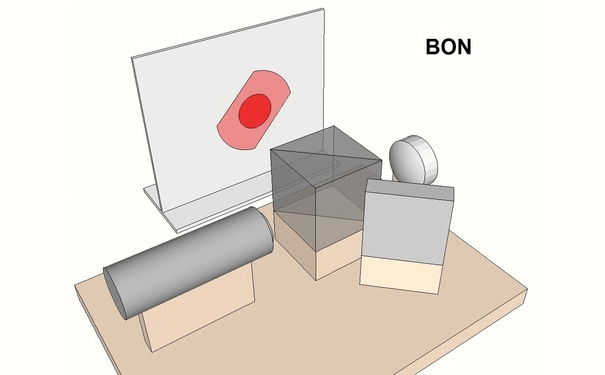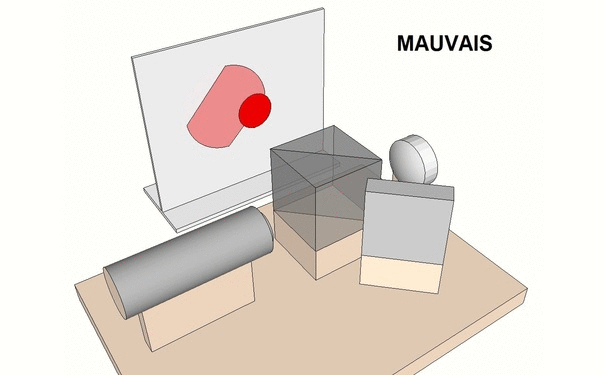
• Installer l’appareil photographique et procéder aux premiers réglages. Une alimentation sur secteur permettra une pleine autonomie dans le cas de longues sessions de prises de vues. Sélectionner le mode Manuel. Choisir un format d’image JPEG avec la meilleure résolution.
• Placer l’objectif au plus près de la face du cube séparateur pour éviter un vignetage éventuel. Il devra ensuite être collimaté sur le faisceau afin d’éviter une ovalisation des interférogrammes pouvant entraîner un astigmatisme de montage. Il convient tout d’abord de centrer le faisceau dans la pupille d’entrée de l’objectif. On peut s’aider pour cela d’un disque en carton placé devant l’objectif dont on aura matérialisé le centre par une croix (voir image ci-dessous à gauche). Si les réglages précédents ont été correctement effectués, on devrait observer sur cet écran deux plages lumineuses circulaires et superposées ayant des dimensions différentes. La plus petite et la plus lumineuse délimite la surface utile du miroir testé. C’est elle qu’il conviendra de centrer dans l’écran de l’objectif en translatant et orientant l’appareil photo. Pour collimater l’objectif, on activera le mode live view de l’appareil, et on fera en sorte de centrer la plage brillante dans l’image. Pour se faciliter la tâche, on peut connecter l’appareil à un ordinateur et le piloter via un logiciel tel que digiCamControl (Les fonctionnalités de ce programme seront utilisées dans le reste de l’exposé. Voir le lien de téléchargement dans le paragraphe « Ressources »). On active la fenêtre de visualisation de l’image en live view via l’icône « Lv » et on peut faire apparaître un réticule en sélectionnant « Affichage / Grille / Split » qui servira de repère de centrage (voir image ci-dessous à droite). Pour ce réglage, il convient à la fois de centrer le faisceau dans l’ouverture de l’objectif et l’image du miroir dans la matrice de l’appareil de prise de vue. On vérifiera enfin que la netteté est homogène sur la circonférence complète de l’interférogramme. Si ce n’était pas le cas, on pourrait soupçonner un défaut d’alignement de l’objectif photo (de type tilt).

On peut ajuster la luminosité de l’image si nécessaire à l’aide du curseur disponible dans le cadre « Affichage ».

• Régler les paramètres de prise de vues dans le cadre « Contrôler » : Ouverture du diaphragme maximum, sélectionner le sensibilité native de l’appareil photo utilisé (100 ou 200 ISO selon la marque), balance des blancs « Manuel », compensation d’exposition « 0.0 ». Déconnecter la correction gamma interne à l’appareil photo si cette option est disponible. Il s’agit ici d’obtenir la réponse la plus linéaire possible dans la restitution des images.
• Peaufiner la mise au point. Pour cela, on utilisera le zoom 5x dans la visualisation live view de digiCamControl (Display / Lv zoom ratio / 5x). Le rectangle matérialisant le champ du zoom 5x sera positionné dans une partie de l’image facilitant la mise au point (bord du miroir, patte de fixation, reflets poussières, …). Pour cela, il suffit de cliquer dans cette zone puis de sélectionner le zoom 5x. Les copies d’écrans ci-dessous donnent une illustration de ces fonctionnalités :

On utilise ensuite les boutons de mise au point en bas de l’image. On dispose de 3 niveaux de mise au point par sens dont on peut éventuellement modifier les pas dans SETTINGS / Live view.

On vérifiera que la netteté est homogène sur la circonférence complète de l’interférogramme. Si ce n’était pas le cas, on pourrait soupçonner un défaut d’alignement de l’objectif photo (de type tilt).

• Vérifier que les reflets internes au cube ne se trouvent pas dans l’aire de l’interférogramme. Si c’était le cas, il conviendrait de mofifier légèrement l’orientation du cube séparateur (un angle de 5° est généralement suffisant pour rejeter les spots lumineux hors de la zone des franges). Il convient ensuite de reprendre les réglages précédents en commençant par le centrage approximatif du spot sur le miroir testé et le parallélisme des faisceaux.
• Réaliser un premier cliché afin de situer la position de l’interféromètre et envisager les ajustements nécessaires. On trouvera ci-dessous une description des aspects d’interférogrammes qu’il est probable d’obtenir pour un miroir asphérique, ainsi que leur analyse (dans le cas contraire, les réglages précédents seront à reprendre avec plus de rigueur) :

	Forme « d’œil de bœuf » centré. On est sur ou très proche du focus 0 (donc au centre de courbure du miroir) et centré sur l’axe optique.Un miroir asphérique contrôlé au centre de courbure présente par définition une aberration sphérique qui se traduit par la présence de ces anneaux. Dans le cas d’un miroir sphérique, aucun anneau ne serait visible au plus proche du focus. Pour obtenir un interférogramme exploitable, il conviendra de déplacer légèrement l’interféromètre en extra-focal (plage exploitable plus large qu’en intra-focal) et en tilt (droite ou gauche ou haut ou bas).
	On est ici toujours très proche du focus 0 mais avec un léger tilt en X. L’axe optique se situe dans cet exemple légèrement vers la gauche. Pour obtenir un interférogramme optimal, il faudra également se déplacer en extra-focal et en tilt. Même s’il ne présente pas les critères requis pour générer une analyse de qualité, on peut malgré exploiter cet interférogramme avec le logiciel de modélisation afin de calculer les valeurs de défocus et de tilt qui aideront à poursuivre le positionnement (voir détail des fonctions plus bas). Il est plus facile d’avoir en point de repère de départ l’œil (axe optique) dans l’interférogramme pour guider les déplacements ultérieurs.
	Cet interférogramme est centré sur l’axe optique mais comporte bien plus d’anneaux que dans le premier cas. On est ici en position extra-focale. Le nombre d’anneaux indique que la défocalisation en extra est trop importante. Il conviendra donc de déplacer l’interféromètre en Z dans le sens intra-focal.
	L’interférogramme ci-contre représente une simulation au même focus que précédemment mais avec un tilt en x. L’axe optique reste toutefois visible dans l’interférogramme. Si le nombre de franges n’est pas trop élevé au point de priver l’interférogramme de contraste suffisant, on pourra également tenter dans ce contexte une modélisation sur le logiciel d’analyse afin de connaître les positions en défocus et en tilt (voir détail des fonctions plus bas).

La stratégie de départ pour le positionnement de l’interféromètre va donc consister à tenter de se situer dès les premières prises de vues au plus proche du focus (valeur proche de 0) et grossièrement sur l’axe optique pour ensuite se déplacer en extra-focal puis en tilt (X ou Y ou les deux à la fois). Même si les premiers interférogrammes manquent d’orthodoxie, on pourra tout de même les exploiter avec le logiciel d’analyse pour en déduire à minima le tilt et surtout le défocus. La valeur idéale de ce dernier se situe aux alentours de 3λ en extra-focal. Nous verrons dans le chapitre suivant comment évaluer cette valeur à partir de l’analyse d’un interférogramme via le logiciel DFTFringe. Le tilt sera quant à lui poussé jusqu’à obtenir entre 30 et 50 franges pour un fonctionnement optimisé de l’algorithme de calcul du front d’onde. On évitera autant que possible les franges en boucle. Il conviendra d’ajuster finement les mouvements de focus et de tilt par itérations et compromis jusqu’à obtenir la forme et le nombre de franges optimums. Cet exercice devient de plus en plus délicat avec des miroirs de plus en plus grands et au rapport F/D de plus en plus faible.

On peut donner à titre d’exemples quelques figures d’interférogrammes plus ou moins exploitables :

	Nombre de franges : L’interférogramme réel ci-contre (en haut) comporte un trop grand nombre de franges (environ 200!). La conséquence est que l’interférogramme manque cruellement de contraste ce qui fera échouer l’algorithme d’analyse de la forme. En se rapprochant du focus ou en recentrant le tilt (ou les deux à la fois) on limitera le nombre de franges. A l’inverse, sur le deuxième interférogramme virtuel ci-contre, on dénombre peu de franges (14). Cette configuration ne fera pas obstacle à une modélisation de la forme. Par contre, l’échantillonnage étant réduit, on va perdre en précision d’analyse notamment sur les défauts de haute fréquence. En fonction de la qualité intrinsèque des interférogrammes, on peut raisonnablement viser entre 30 et 50 franges. Avec des interférogrammes de qualité, on peut même sensiblement augmenter ce nombre.
	Linéarité des franges : Le logiciel de traitement des interférogrammes s’accommode mal de franges en boucle voire trop incurvées. Dans l’exemple ci-contre (en haut) on peut voir une frange en boucle fermée (à 3h) et une ou deux franges relativement incurvées à l’opposé. Ces structures vont générer des artefacts de calcul et se traduire par des creux ou des bosses virtuelles qui vont entacher la précision de la forme réelle du front d’onde (surtout dans le cas des boucles). Pour palier ce phénomène, on va donner plus de tilt en décalant légèrement l’interféromètre en X ou Y. Ce faisant, on va automatiquement redresser les franges mais également les resserrer ( voir deuxième exemple ci-contre). Ainsi, en poussant le tilt jusqu’à éliminer les franges circulaires, on risque  de faire chuter le contraste à un niveau critique en augmentant le nombres de franges. Malgré tout, avec de grands miroirs ouverts, il est difficile (et parfois impossible) d’arriver à un compromis entre la linéarité des franges et leur nombre. Dans ce cas, on neutralisera les effets de ce défaut en moyennant plusieurs fronts d’ondes orientés différemment ou en excluant du calcul la zone de l’interférogramme contenant les boucles (à condition de s’être assuré préalablement qu’elle ne contient pas d’autres défauts réels significatifs). Ces fonctions seront décrites dans le chapitre « Analyse des interférogrammes » ci-dessous.
	Exemples d’interférogrammes parfaitement exploitables : Les deux interférogrammes ci-contre (virtuel pour le premier, réel pour le second) comptent 44 franges dont la forme est peu incurvée. Ils seront donc parfaitement adaptés à une analyse par le logiciel de calcul de fronts d’ondes. Il est toutefois à noter que le rapport F/D = 5 est favorable à cette configuration. Avec des miroirs plus ouverts et/ou plus grands, il sera souvent impossible d’atteindre ce résultat. Il faudra alors trouver le meilleur compromis entre le nombre de franges et leur courbure.

Le programme DFTFringe propose également des simulations d’interférogrammes à partir de données paramétrables (défocus, tilt, …). On pourra ainsi se familiariser avec les différents aspects de ces interférogrammes virtuels et les comparer à ceux enregistrés lors des tests. Cet outil sera ainsi d’une aide précieuse pour guider l’utilisateur sur l’amplitude et le sens des ajustements à envisager.

---

–

 

 

 

Analyse des interférogrammes :

 

Parmi les quelques logiciels d’analyse d’interférogrammes disponibles, nous conseillerons  DFTFringe de Dale Eason pour plusieurs raisons :

• Il est un des plus performants, si ce n’est le plus performant
• Il est particulièrement ergonomique
• Il est gratuit
• Il bénéficie d’un support technique interactif et très efficace, notamment de la part de son auteur en personne, sur le groupe de discussions “Interferometry”

Se reporter au paragraphe « Ressources » pour le lien de téléchargement et celui du groupe de discussions.

Nous allons passer en revue chaque étape de son utilisation.

 

Configuration :

Il convient tout d’abord de paramétrer certaines données de base. Pour cela, on active le menu « Configuration / Mirror ».

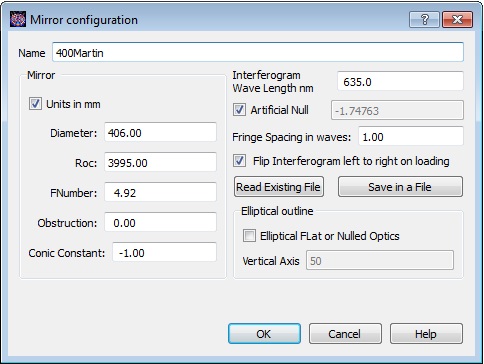
Name : Donner un nom explicite ou une description plus complète (nombre de caractères non limité par le champ).

Units in mm : Cocher cette case pour saisir les valeurs en mm (à défaut l’unité sera le pouce)

Diameter : Saisir le diamètre optique. Cette donnée doit être la plus précise possible. Des décimales peuvent être saisies.

Roc : Saisir le rayon de courbure paraxial du miroir (rayon de la zone centrale). Cette donnée devra également être relativement précise.

Fnumber : Le rapport d’ouverture relative se calcule automatiquement.

Obstruction : Il est possible de neutraliser une partie centrale du front d’onde calculé. Cette option peut être utilisée pour ignorer la zone centrale obstruée par le miroir secondaire.

Conic Constant :  Saisir ici le coefficient de la conique associée à la forme du miroir (ex : -1 pour une parabole, 0 pour une sphère).

Interferogram Wave Length nm : Saisir la longueur d’onde (en nanomètres) du laser utilisé pour le contrôle.

Artificial Null : Cocher cette case si le test est effectué au centre de courbure. Le logiciel calculera alors l’aberration de sphéricité induite par cette configuration (valeur à droite) et la retirera du front d’onde brut.  On décochera cette case dans le cas d’un test en auto-collimation, Dall null test ou le Ross null test.

Fringe Spacind in waves : En général, la valeur requise est 1 (1 longueur d’onde pour un inter-frange).

Flip Interferogram left to right on loading : Selon sa configuration, l’interféromètre de Bath provoque un effet « miroir » droite / gauche des images d’interférogrammes exactement comme dans un télescope de type Newton (c’est le cas du modèle à angle droit classique). Pour que les fronts d’ondes modélisés soient fidèles à la réalité il convient donc, s’il y a lieu, de cocher cette case. En cas de doute, on matérialisera un repère sur l’image (petit masque en débord par exemple) pour voir s’il est, ou pas, inversé par rapport à la réalité.

Save in a File : Il est souhaitable de sauvegarder ces données dans un fichier dont le nom devra être explicite.

Read Existing File : Les fichiers sauvegardés pourront ainsi être chargés évitant ainsi une nouvelle saisie des données.

 

Ouverture d’un interférogramme :

L’ouverture d’un interférogramme se fait via le menu « Files / Load Interferogram » ou à l’aide de l’icône .

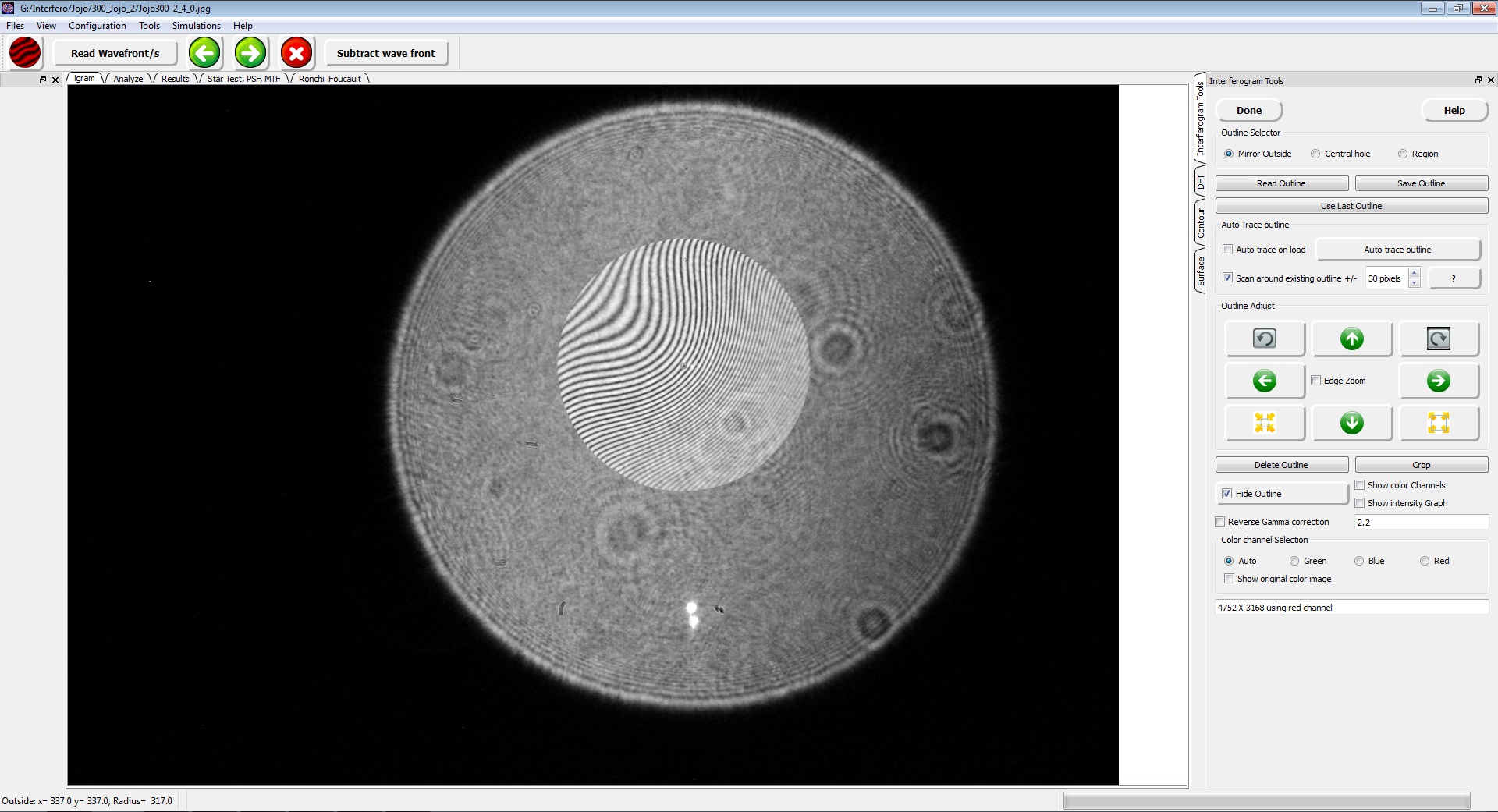
Après sélection d’un fichier, la fenêtre suivante apparaît :

Par défaut, l’image est affichée en noir et blanc afin de rendre plus performant l’outil de détection automatique du contour du miroir. On peut toutefois retrouver les couleurs originales en cochant la case « Show original color image ».

 

Définir le contour du diamètre optique :

Il faut ensuite indiquer au logiciel la partie utile de l’image qui sera analysée et qui  correspond au diamètre optique du miroir. Pour cela, le logiciel propose des outils performants :

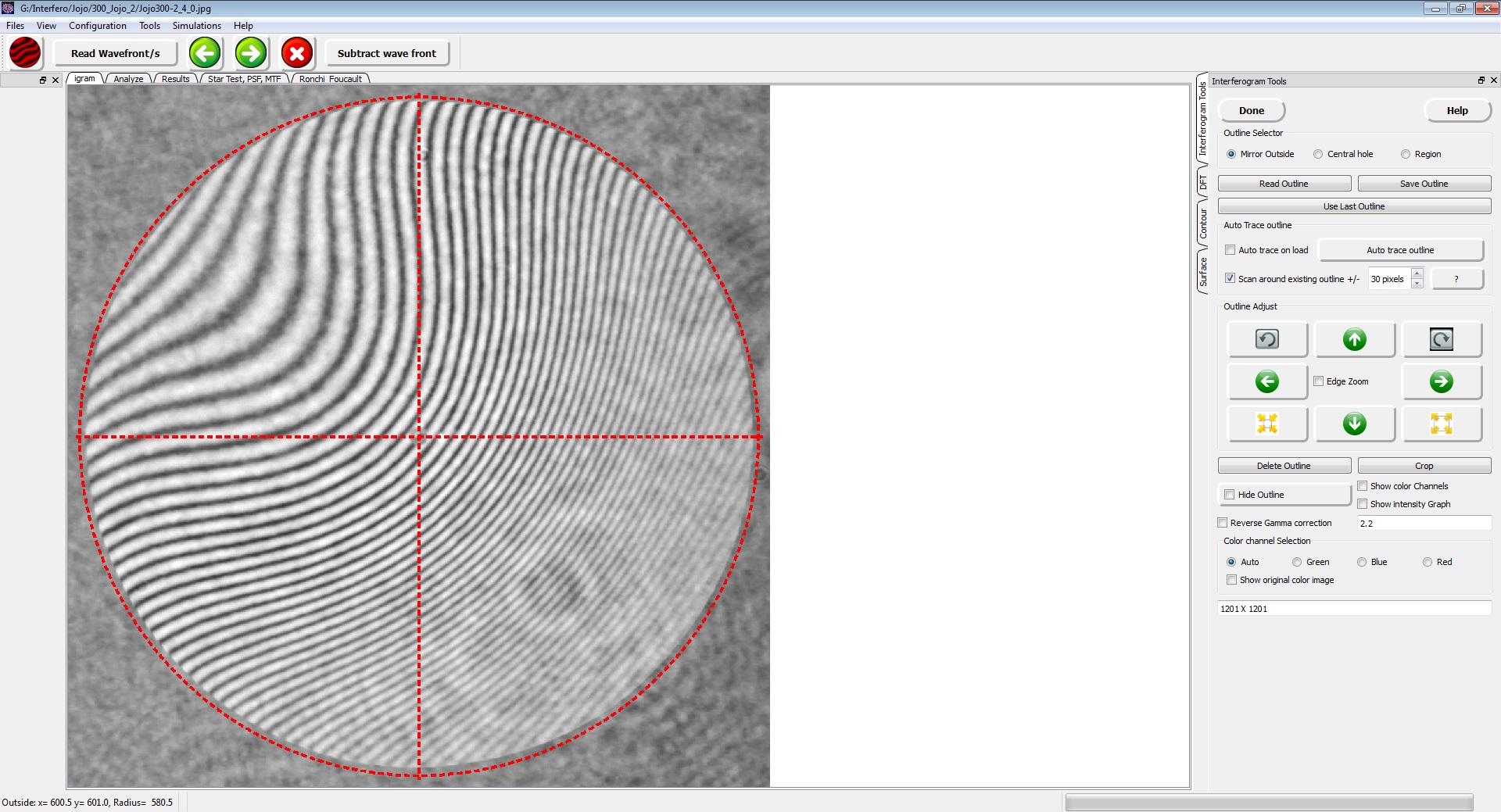
Un cercle virtuel devra être parfaitement superposé au diamètre optique matérialisé par le bord de l’interférogramme. Pour le faire apparaître, il faut valider les options suivantes :

• Dans le cadre « Outline Selector » en haut à droite, on sélectionne « Mirror Outside » si ce n’est pas déjà fait
• On décoche la case « Hide Outline » située plus bas

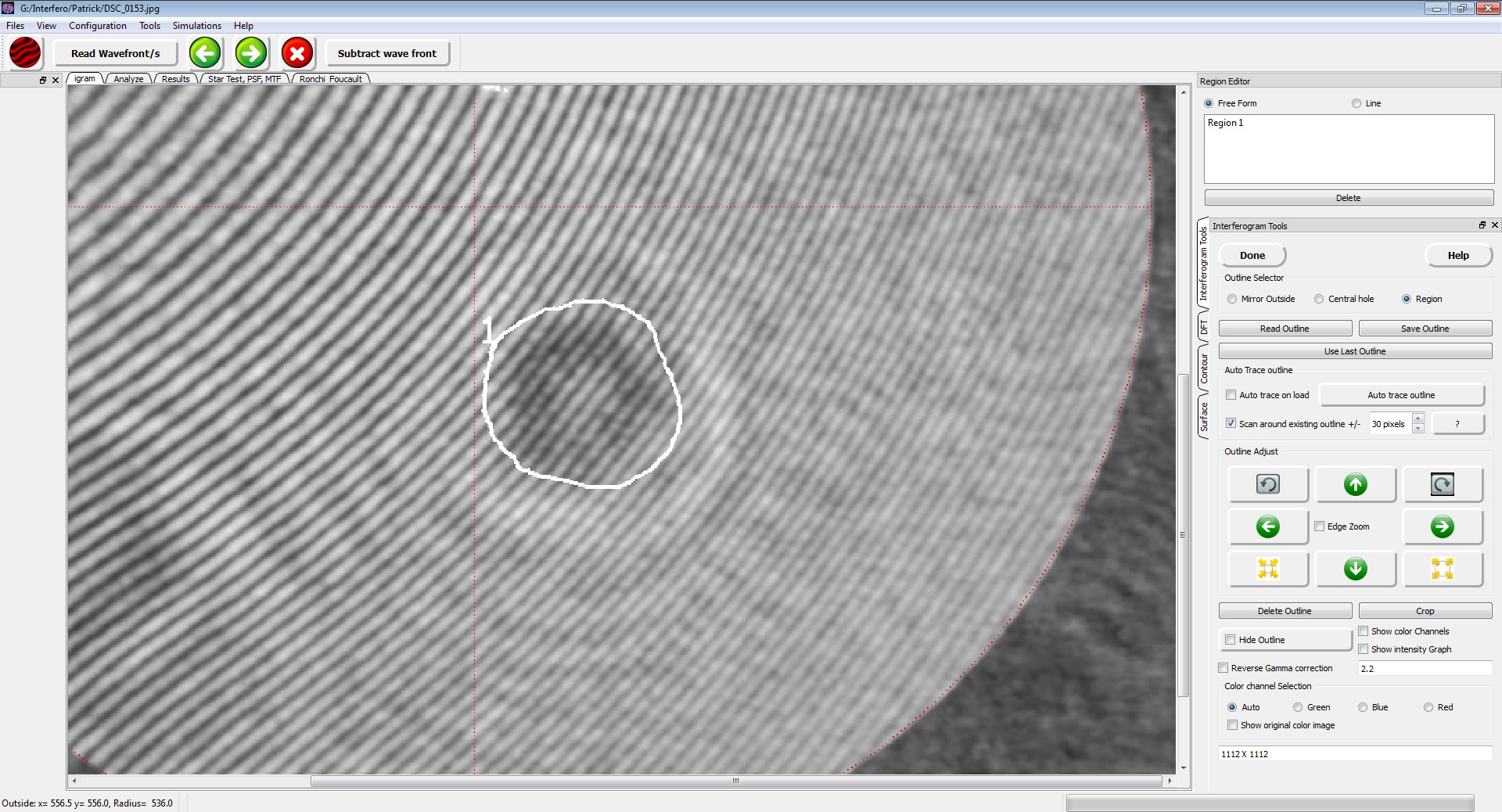
Pour positionner le cercle sur l’image, on clique sur le bord de l’interférogramme à la position 9h puis, sans relâcher, on glisse le pointeur dans la position diamétralement opposée (3h). Dans un premier temps, on inscrira volontairement un cercle un peu plus grand que l’interférogramme. On clique ensuite sur le bouton « Crop » ce qui va générer un fenêtrage limité à la zone ainsi définie.

On s’assurera que la partie utile de l’interférogramme est entièrement contenue dans la fenêtre cropée. A défaut, il faudra recommencer la procédure de positionnement du contour. On clique ensuite sur le bouton « Auto trace outline » qui va démarrer une routine de positionnement automatique du contour de la ligne au bord de l’interférogramme. Cette routine peut être déclenchée automatiquement à chaque ouverture d’interférogramme en cochant la case “Auto trace on load”.

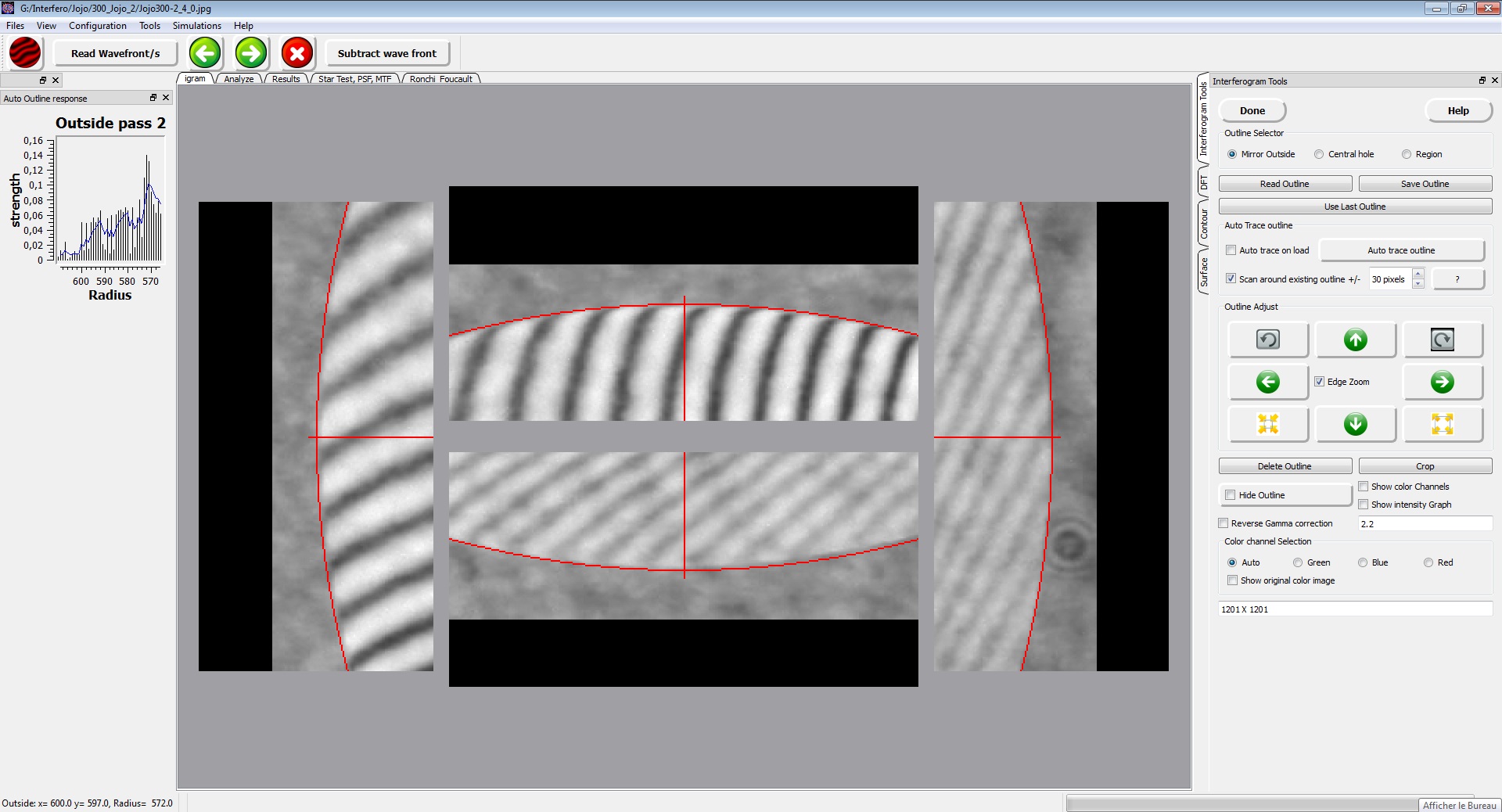
La précision de cette procédure n’est pas toujours garantie et il convient donc de la vérifier. Pour cela, on coche la case « Edge Zoom » pour faire apparaître 4 petites fenêtres correspondant aux zones 0h, 3h, 6h et 9h du bord de l’interférogramme zoomé. Au besoin, on peut modifier encore le zoom avec la molette de la souris.

Avec une ligne de contour de 1 pixel de large, le bord des franges doit juste tangenter côté intérieur du cercle virtuel. La précision de ce positionnement a une grande influence sur la fiabilité des résultats, en particulier pour des miroirs ouverts pour lesquels un positionnement à 1 pixel près est souhaitable. On ajustera donc au mieux en procédant de la façon suivante :

• On pourra déplacer le cercle dans les quatre directions à l’aide des flèches vertes situées sur la droite.
• On pourra augmenter ou diminuer le diamètre du cercle avec les flèches jaunes.
• On ajustera le niveau de zoom optimal avec la molette de la souris.
• On choisira les caractéristiques de la ligne de contour les plus adaptées. Pour cela on sélectionnera le menu « Configuration / Preferences / Interferogram ».
  
• On ajustera au besoin la taille des fenêtres en nb de pixels dans le champ “Zoom Box width”.

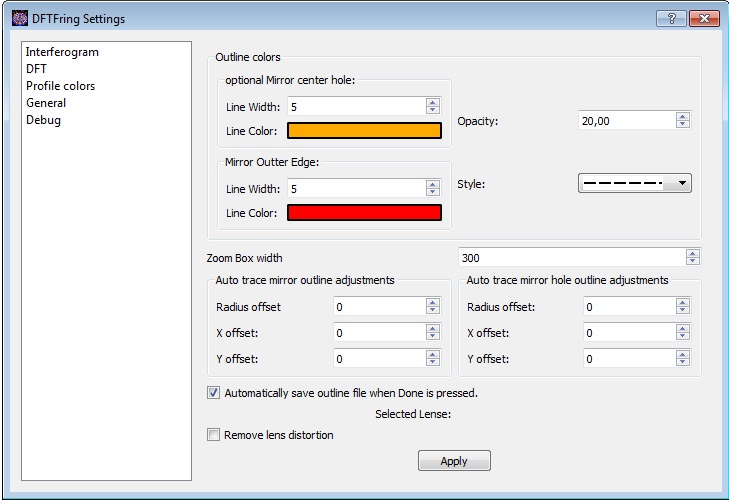
Les options suivantes peuvent apporter un plus :

Largeur de ligne : 5 pixels
Opacité : 20%
Type de ligne : Petits tirets
Couleur : Teinte contrastée (rouge par exemple si image en noir et blanc)
On positionnera le cercle de telle manière que le contour de l’interférogramme soit juste à l’extérieur du milieu de l’épaisseur des tirets :

Il est parfois plus facile de situer le bord de l’interférogramme par transparence du cercle par-rapport à sa demi-épaisseur que de comparer à une ligne fine. Une apparence de 1 pixel de large, en petits tirets à 100% d’opacité donne également de bons résultats mais est difficilement repérable au zoom minimum. On pourra enfin faire apparaître et disparaître le cercle par séquences rapides en cliquant sur le bouton « Hide Outline » ce qui aidera à mieux apprécier le positionnement optimal de la ligne.

A ce stade, on pourra également vérifier la circularité de l’interférogramme. En effet, une ovalisation de celui-ci sera immédiatement perceptible au travers des écarts constatés sur les axes horizontal et vertical. Cette déformation trouve en général son origine dans un défaut d’alignement de l’objectif photo. Dans ce cas, il conviendra de reprendre ce réglage au risque de générer un défaut d’astigmatisme de montage qui n’a pas lieu d’être et susceptible de fausser l’estimation de la précision du front d’onde.

En présence d’un miroir troué, on matérialisera de la même manière le contour de celui-ci en sélectionnant « Central hole » dans le cadre « Outline Selector ». La procédure de positionnement du contour est ensuite la même que pour le bord extérieur.

 

Réglage de la photométrie :

La photométrie des interférogrammes doit être maîtrisée afin d’éviter des corrections gamma automatiques de l’appareil photo susceptibles de générer des artefacts (voir paragraphe « Principales causes d’imprécision » plus haut).

DFTFringe dispose d’un outil de coupe photométrique qui permet d’analyser finement les images. Pour l’activer, le cercle de contour étant préalablement bien positionné, on coche la case « Show intensity Graph » :

Un graphique apparaît alors avec les courbes photométriques des trois couleurs. On s’intéressera à la couleur dominante liée à la longueur d’onde du laser utilisé (ici le rouge). Un cadrant permet d’orienter la coupe perpendiculairement aux lignes de franges. L’amplitude de la courbe devrait idéalement se situer en gros dans la première moitié de l’échelle des niveaux de gris (0 à 128 niveaux). Dans l’exemple ci-dessus, on voit que l’intensité globale est trop élevée approchant même la saturation dans ses niveaux les plus hauts. Il convient donc d’abaisser la luminosité de l’interférogramme :

• Soit en diminuant le temps de pose
• Soit en réduisant le flux du laser quand cela est possible (laser rouge uniquement, électronique associée).

En présence de franges peu contrastées ou diffusantes (du fait par exemple d’un mauvais état de surface optique), le logiciel peut avoir des difficultés à analyser les parties de l’Igram où les franges sont relativement resserrées. Dans ce cas on peut tolérer de relever le niveau photométrique d’ensemble pour gagner en contraste.

 

Modélisation du front d’onde et résultats :

Les étapes précédentes ayant été menées correctement, on va pouvoir lancer les calculs en cliquant sur le bouton « Done ». La fenêtre suivante apparaît alors :

Pour comprendre un minimum l’aspect énigmatique de la figure qui apparaît suite au calcul du logiciel, il convient de dire un mot succinct sur le processus qui a été mis en œuvre à ce stade. L’image de départ de l’interferogramme appartient au domaine « spatial », c’est à dire qu’à chaque pixel d’une intensité lumineuse donnée sont affectées des coordonnées dans l’espace cartésien. L’intérêt de passer du domaine « spatial » au domaine « fréquentiel » réside dans le fait que les traitements appliqués à l’image seront plus rapides et plus performants. L’algorithme de calcul, en l’occurrence une Transformée de Fourier Rapide (FFT en anglais) va transposer cette image dans le domaine « fréquentiel ». Ici, l’image « spatiale » va être analysée puis matérialisée dans un graphique en fonction de la fréquence spatiale  de groupes de pixels de différentes dimensions dans un intervalle donné. Dans cette image « fréquentielle », les basses fréquences seront matérialisées au centre et les hautes fréquences vers le bord. Dans notre exemple, on constate la présence de deux disques brillants de part et d’autre du centre qui rappellent l’aspect des plages intra et extra d’un startest d’étoile. Ces « lobes latéraux » sont en fait  la représentation fréquentielle des franges de l’interférogramme. Plus leur diamètre est grand, plus le défocus de l’interférogramme est élevé. Plus les franges sont nombreuses (et donc resserrées), plus les lobes sont éloignés du centre (haute fréquence).  On distingue souvent (c’est le cas ici) des lobes secondaires plus éloignés du centre. Il sont à l’origine d’artefacts dans la modélisation du front d’onde (en particulier le « print through). Dans la partie centrale (intérieure aux lobes principaux) se trouve le bruit de fond de basse fréquence intrinsèque à l’image de l’interférogramme. Ce bruit peut biaiser les résultats et il est souhaitable de l’éliminer en le filtrant. C’est l’objet du disque sombre au centre de l’image fréquentielle de l’interférogramme. Il va servir à matérialiser la zone de basse fréquence à filtrer. Il appartient à l’utilisateur de la dimensionner correctement. Pour cela, il suffit de cliquer sur la circonférence de ce disque et de la faire tangenter aux lobes latéraux sans empiéter dessus (voir exemple ci-dessous). Heureusement, il n’est pas nécessaire d’être un expert du domaine fréquentiel pour réaliser le traitement de l’image ! Il suffit simplement de réaliser la petite manipulation précédente.

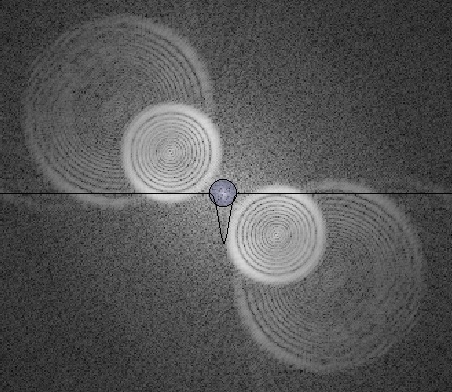
Il est maintenant enfin possible de calculer le front d’onde et de visualiser les premiers résultats. Pour cela, on clique sur le bouton « Compute Surface ». Après quelques secondes, la fenêtre suivante apparaît :

Passons en revue les principales informations qui y figurent :

• Image 3D du front d’onde :

Cette fenêtre permet de visualiser l’aspect du front d’onde en 3D. Il est possible de modifier l’orientation de la figure avec un cliquer-glisser. Un clic droit donne accès à une visualisation plein écran (retour à la visualisation initiale par clic droit). On peut zoomer avec la mollette de la souris. On peut modifier l’orientation de la figure avec un cliquer-glisser. Des grilles d’échelle sont visibles en arrière plan. Un bandeau supérieur donne accès à certains paramètres modifiables : échelles (longueur d’onde de référence : 550 nm), sauvegardes d’images et de vidéos. On peut juger de la qualité globale d’une modélisation de front d’onde de deux manières :

– Visuellement en repérant des accidents anormaux de la forme (pentes brusques, très localisées, …)

– En utilisant l’outil « View / Show unwrap errors ». Il fait apparaître une carte indiquant les zones où le logiciel a généré des erreurs (pixels blancs). Elles ont souvent pour origine le manque de contraste des franges. Leur nombre est indiqué dans le bandeau supérieur et témoigne de la fiabilité du calcul. Une valeur supérieure à 1000 devrait logiquement conduire à rejeter l’image. Une valeur inférieure à 100 est un bon résultat, inférieure à 10 excellent. Au delà du nombre, il faut également porter un jugement sur le niveau de concentration de ces défauts. S’ils sont diffus sur l’ensemble du disque, ils sont moins pénalisants que s’ils sont regroupés sur une même zone (contours continus comme sur l’image ci-dessous). Pour diminuer le nombre d’erreurs, on augmentera le contraste des franges (luminosité, réduire leur nombre, affiner la mise au point, …).

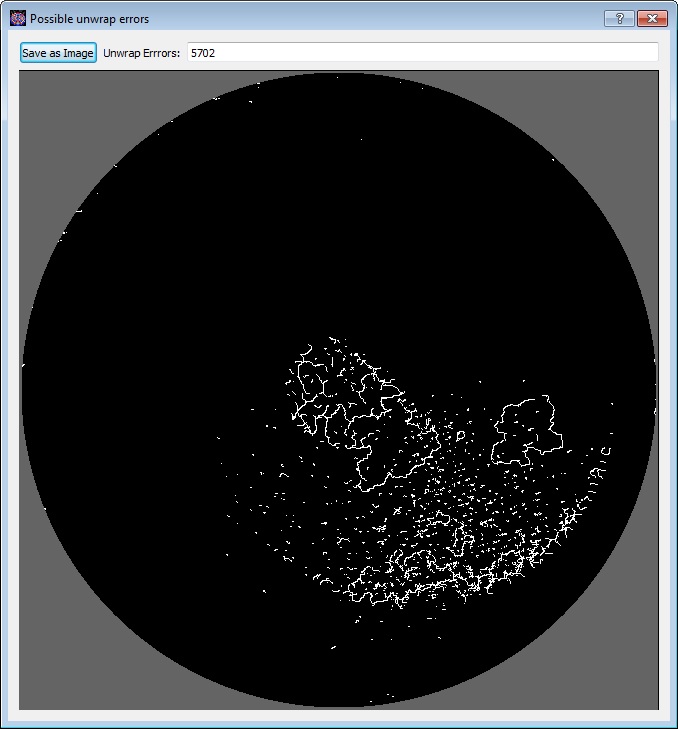
• Cartes de contours :

Visualisation en 2D du front d’onde. Une échelle associe les couleurs aux valeur de fractions de longueur d’onde (à 550 nm). Possibilité également de visusalisation en plein écran.

• Profil de l’onde :

Il s’agit d’une coupe du modèle 3D selon une orientation de méridienne donnée qu’il est possible de faire varier avec le cadran en haut à gauche du graphique. On peut également superposer 16 profils (par pas de 22,5° d’orientation) en cochant le choix « 16 diameters of current wavefront ». Les lignes en tirets rouges délimitent l’amplitude du critère de Rayleigh (λ / 4). Par défaut, l’échelle d’amplitude est exprimée en fractions de longueur d’onde (550 nm). On peut choisir de l’afficher en nanomètres en cochant la case « Show in Nanometers ». Enfin, en cochant la case « Surface error » on remplacera le profil de l’onde par le profil de la surface du miroir (deux fois moins déformé).

• Résultats numériques :

Le résultat des calculs est  détaillé dans le cadre de gauche. :

Wavefront RMS : Précision du front d’onde exprimée en fraction de longueur d’onde RMS (λ / 15,6 RMS dans l’exemple ci-dessus).

Strehl : Rapport de Strehl du front d’onde. Représente donc le pourcentage de rayons émergents contenus dans le diamètre de la tache de diffraction (85% dans l’exemple ci-dessus). C’est l’un des critères les plus déterminants pour quantifier la précision globale du front d’onde.

Le tableau en-dessous détaille les valeurs affectées à chaque terme du polynôme de Zernike. Ce développement en série décompose la forme complexe du front d’onde en autant de défauts standards individuels (aberration sphérique, astigmatisme, …) auquel il affecte une amplitude. Ces défauts sont classés selon leur contribution décroissante au travers d’un « ordre » . Il y a ainsi une infinité de termes mais les algorithmes de calcul se limitent aux premiers ordres qui ont une influence significative sur les résultats réduisant ainsi le temps de traitement sans nuire à la précision. L’autre intérêt de cette formulation est que l’on peut quantifier chaque type de défaut et évaluer sa contribution au résultat final. On peut même neutraliser une partie d’entre eux et en visualiser l’impact. Dans le tableau de DFTFringe, les cases à cocher au droit de chaque terme permettent cette option. Par défaut, les termes « Piston », « Tilt », « Defocus » et « Coma » sont décochés car ils ne sont induits que par le montage et non une aberration propre au miroir. Les boutons « Enable All » et « Disable All » permettent d’activer ou désactiver automatiquement tous les termes sauf les quatre mentionnés ci-dessus. Cette fonction peut par exemple permettre de neutraliser l’astigmatisme d’ordre supérieur quand ce défaut est imputable à une pliure du miroir sur son support de contrôle (à manier avec précaution). La colonne de droite donne les valeurs des défauts RMS pour chaque terme. La précision globale RMS affichée plus haut est la somme de chacun de ces termes. La colonne « Wyant » donne quant à elle des valeurs PTV.

Les valeurs des termes Wyant « Defocus » et « Tilt », même si elles n’entrent pas dans le calcul final, ont malgré tout une réelle utilité. En effet, elles permettent de connaître précisément la position de l’interféromètre et donc d’affiner les réglages initiaux :

– Defocus : Une valeur négative indique une position intra-focale. On a vu précédemment qu’il était préférable de réaliser les interférogrammes en position extra-focale. Dans ce cas, on éloignera l’interféromètre pour atteindre une valeur Wyant aux alentours de +3,000. Ceci n’est qu’une approximation dont l’expérience a montré qu’elle produisait des interférogrammes plutôt optimisés. Elle est à adapter au cas par cas notamment pour de petits miroirs peu ouverts. Dans l’exemple ci-dessus (miroir de 306 mm à F/D = 4,9), la valeur de défocus a été calculée à +5,805 alors que l’interférogramme a malgré tout été pleinement exploitable.

– Tilts : Les valeurs de tilt sont données sur chacun des axes (x et y). La valeur absolue globale est donc  . On peut ainsi mettre en évidence des décalages excessifs que l’on rectifiera lors des réglages.

Il arrive parfois qu’un message d’alerte apparaisse en cours de calcul de front d’onde, à savoir : « Wavefront seems inverted. Do you want to invert it ? ». Dans certaines configurations particulières, le logiciel ne sait pas analyser dans quel sens il doit orienter le front d’onde et demande dans ce cas à l’utilisateur s’il doit l’inverser. Dans le cas d’un miroir asphérique, on répondra « Yes » à l’invite. Pour les miroirs sphériques, la bonne réponse est beaucoup plus complexe à identifier et en cas de mauvaise option, cela peut générer une aberration sphérique susceptible de fausser artificiellement les résultats. Pour savoir si le front d’onde qui a finalement été généré est dans le bon sens, Dale Eason propose une petite manipulation qui consiste à appliquer le pouce quelques secondes sur une région de la surface optique afin de générer un effet thermique. Un nouvel interférogramme est ensuite rapidement enregistré et calculé sur les mêmes bases que le précédent. Si le défaut ainsi créé est une bosse, le front d’onde est bien orienté. Dans le cas contraire, il faudra l’inverser. L’inversion peut être opérée à tout moment à l’aide du bouton « Invert » dans l’onglet « Surface ». Dans le cas d’un miroir asphérique, on peut vérifier dans « Configuration / Mirror » que le signe affecté au coefficient de la conique est le bon (c’est à dire négatif).

Une fois calculés et validés, on va sauvegarder chacun des fronts d’ondes via le menu « Files / Save Wavefronts ». On choisira un nom de fichier explicite, par exemple GAP300_2_90 pour le deuxième front d’onde à l’orientation 90° du miroir sur son support de contrôle.

 

Moyenne des fronts d’ondes :

Pour gagner en précision, il est nécessaire de multiplier les mesures et de les moyenner. Cela permettra de lisser les effets des artefacts d’interférogrammes (le « Print through » par exemple) et de réduire le niveau de bruit. Pour ce faire, on variera à chaque prise de vue l’inclinaison des franges et un peu leur nombre en jouant sur les réglages de tilt et de défocus (voir exemples ci-dessous). En général, une dizaine d’interférogrammes devrait suffire mais tout dépend de leur qualité intrinsèque. On peut augmenter le nombre de mesures tant qu’il influe significativement sur le résultat.

On va ensuite ouvrir la série de fronts d’ondes pour une orientation donnée du miroir via le menu « Files / Read Wavefronts » avec une sélection multiple des fichiers. Le chargement peut prendre quelques secondes. La liste des fronts d’ondes est visible dans l’onglet « Surface » à droite de la fenêtre du logiciel (voir copie d’écran ci-dessous).

On peut les visualiser successivement en cliquant sur chaque nom de fichier dans le liste. On peut éliminer l’un d’eux de la liste en le sélectionnant et en cliquant sur le bouton : 

Pour effectuer la moyenne de ces fronts d’ondes, on les sélectionne individuellement ou par sélection multiple (Ctrl + clic ou Shift + clic) ou en totalité via le bouton « Select All » puis on clique sur « Average ». Le front d’onde moyen est alors calculé et se rajoute à la liste sous le nom « Average.wft ». La dernière opération consiste à sauvegarder ce front d’onde sous un nom explicite par exemple  GAP300_moy_90 (pour la moyenne des fronts d’ondes d’orientation 90°).

 

Moyennes des orientations :

Réaliser la moyenne de plusieurs orientations du miroir va contribuer à neutraliser (au moins partiellement) certains défauts générés par le supportage du miroir (Astigmatisme de pliure, trefoil de poinçonnement des appuis). Encore faut-il que ces défauts soient suffisamment reproductibles ce qui est loin d’être évident, notamment avec de grands miroirs minces. Il est préalablement nécessaire d’établir un protocole de rotation du miroir pour une bonne prise en compte dans le traitement informatique. On aura préalablement tracé précisément des repères angulaires sur la tranche du miroir (séparés de 90° dans l’exemple ci-dessous) et installé un curseur sur le support de contrôle. Les repères sont gradués dans l’ordre croissant des valeurs angulaires dans le sens inverse des aiguilles d’une montre. On passe donc de la position 0° à la position 90° du miroir en tournant celui-ci de 90° dans le sens des aiguilles d’une montre (voir figure ci-dessous).

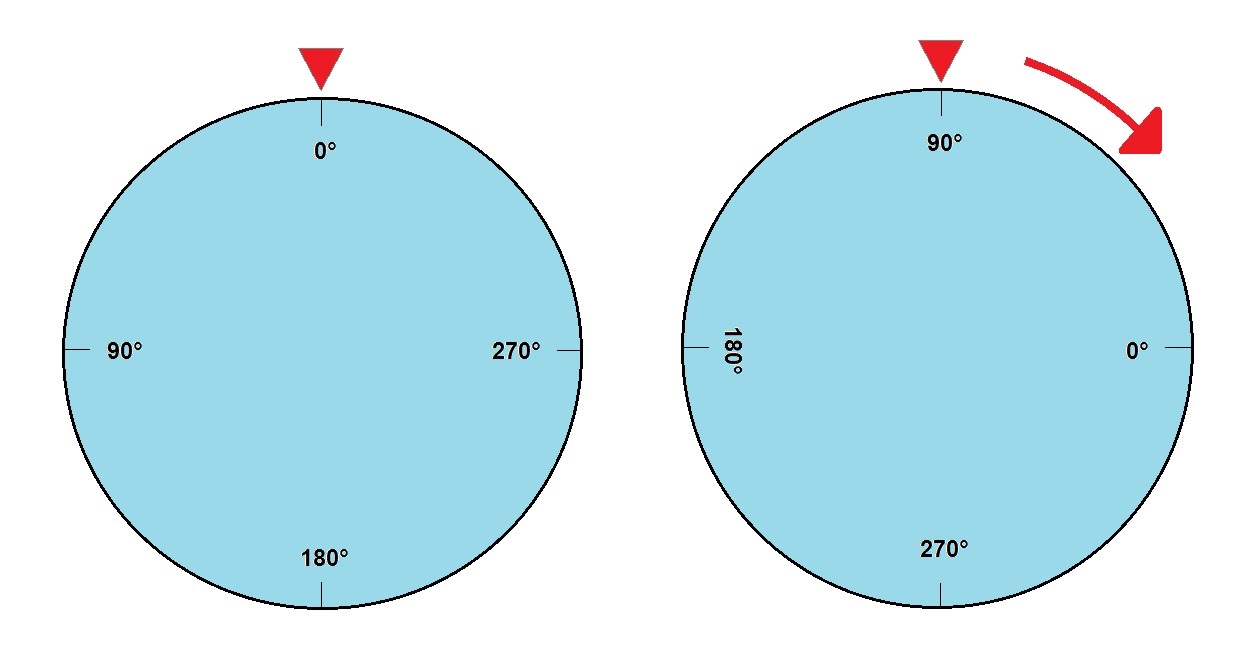
Les séries de fronts d’ondes pour une orientation donnée auront été moyennées et sauvegardées comme décrit dans le paragraphe précédent. On va ensuite ouvrir les différents fichiers de fronts d’ondes moyens orientés via le menu « Files / Read Wavefronts ». Le front d’onde moyen relatif à l’orientation 0° ne subira aucun traitement. Par contre, il faudra « dérotater » les autres pour les repositionner dans l’orientation 0° de départ. Pour cela, on procède de la manière suivante :

On sélectionne les orientations les unes après les autres et on clique sur le bouton « Rotate ». La boite de dialogue propose de saisir un angle et un sens. L’angle sera celui de la rotation du miroir (270° dans l’exemple ci-dessus). Pour le sens de rotation, il doit être inverse à celui dans lequel le miroir a été tourné. Il convient de distinguer deux cas de figure :

• Si la case « Filp Interferogram left to right on loading » a été cochée dans la boite de dialogue « Mirror configuration », il faut cocher la case « CCW »
• Sinon, il faut décocher la case « CCW »

Le logiciel procède alors au traitement de « dérotation » et génère un nouveau front d’onde en intégrant à la fin du nom l’indication du sens et de la valeur angulaire de la rotation opérée.

Il reste alors à moyenner le front d’onde 0° (n’ayant subi aucune rotation) et les autres fronts d’ondes « dorotatés via une sélection des fichiers et un clic sur « Average ». Un nouveau front d’onde moyen est alors généré et nommé « Average.wft ». Il convient enfin de le sauvegarder sous un nom explicite, par exemple GAP300_moy_0_90_180_270.

 

Analyse et retrait des effets induits par le support de contrôle :

Comme on vient de le voir, moyenner plusieurs orientations du miroir permet de neutraliser autant que possible les défauts induits par le support de contrôle (astigmatisme de pliure, tréfoil, …). Toutefois, il est nécessaire de s’assurer que ces défauts soient suffisamment reproductibles aux différentes orientations pour valider la fiabilité de ce traitement. Un placement incorrect du miroir sur le support de contrôle ou des veines d’air peuvent par exemple biaiser le traitement de par leur caractère non reproductible. Pour ce faire, le logiciel DFT Fringe dispose d’un outil spécifique particulièrement puissant qui permet une analyse fine des défauts et leur correction. Pour effectuer ce traitement, il convient au préalable de disposer d’au moins 2 moyennes de fronts d’ondes sur des orientations formant un angle de 90° (Pour réaliser les moyennes de fronts d’ondes pour une orientation donnée, se référer au paragraphe précédent). Afin que les résultats soient les plus précis possible, on traitera deux paires de fronts d’ondes à 0° / 90° et 180° / 270° à laquelle on peut idéalement rajouter deux paires à 45° / 135° et 225° / 315° ce qui rendra l’analyse statistiquement plus pertinente. On s’assurera que le nom d’enregistrement de ces fichiers comporte l’angle d’orientation en chiffres.

On pourra alors lancer l’outil via le menu “Tools / Test Stand Astig Removal”. Après avoir passé les pages de commentaires en cliquant sur “Next”, la fenêtre suivante apparaît :

On sélectionne le dossier d’origine des fronts d’ondes pour chaque orientation en cliquant sur le bouton associé au champ “Base path”. On clique ensuite sur le bouton “Add average Wavefront file to List” pour sélectionner les différents fichiers de fronts d’ondes orientés à rajouter dans la liste. La fenêtre suivante apparaît alors :

Il faut renseigner l’angle d’orientation du front d’onde sélectionné. Si cet angle figure dans le nom du fichier, il sera proposé par défaut. Il faut enfin spécifier le sens de “dérotation” à appliquer à ce front d’onde afin de replacer chacun d’eux dans le même référentiel (voir paragraphe précédent pour plus de détails). Une fois que tous les fronts d’ondes sont sélectionnés et paramétrés, on clique sur “Compute”. Le logiciel va alors procéder successivement aux opérations suivantes :

• Dérotation de chaque front d’onde orienté (sauf pour l’orientation 0°)
• Moyenne de tous ces fronts d’ondes “dérotatés”. Elle est nommée “AverageStandRevoved”.
• Soustraction à ce front d’onde moyen de chacun des fronts d’ondes d’une orientation donnée. On obtient ainsi le front d’onde des défauts induits par le support pour chaque orientation.
• Calcul d’un front d’onde “moyen” des défauts induits par le support. Ce calcul consiste simplement en une moyenne arithmétique des fronts d’ondes des défauts induits par le support pour chaque orientation. Il est nommé “Average Stand effects”.

Un rapport est alors généré à l’écran et sauvegardé automatiquement en format pdf sous le nom spécifié dans la fenêtre. Celui-ci présente les résultats d’analyse suivants :

• Fronts d’ondes de chaque orientation avant et après dérotation
• Fronts d’ondes des effets induits par le support pour chaque orientation :

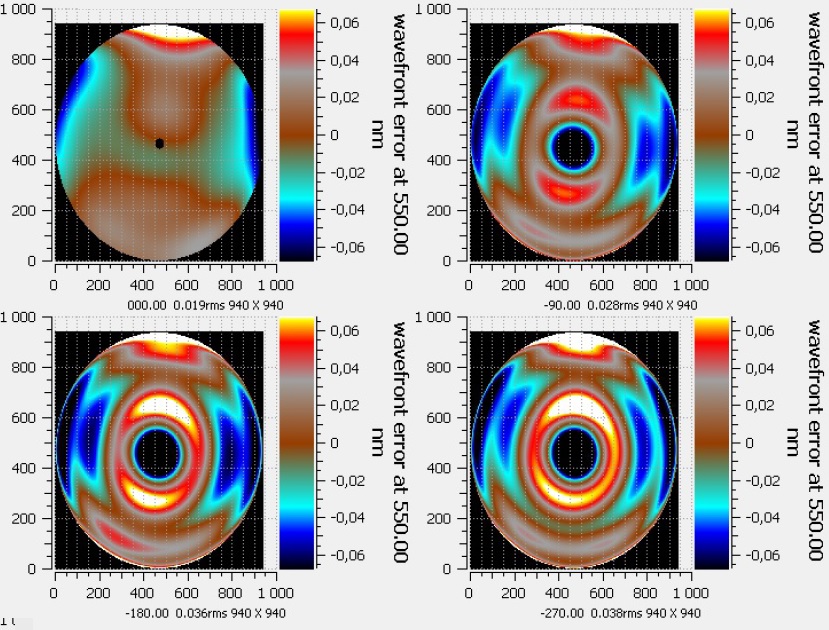
• Front d’onde « moyen » des effets induits par le support
• Un tableau de valeurs et un graphique permettant d’analyser et de calculer les défauts d’astigmatisme induit pas le support de contrôle :

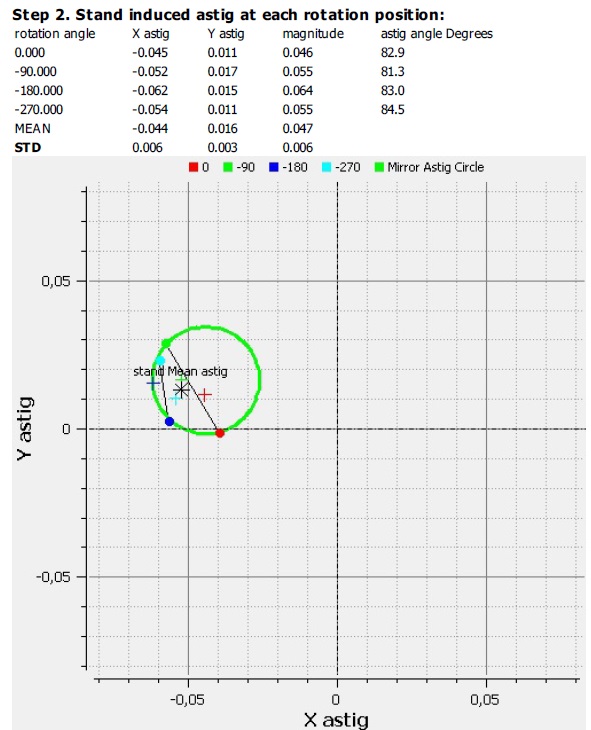
– Pour chaque orientation, le tableau mentionne la valeur des termes de Zernike X astig, Y astig issue du calcul des moyennes de fronts d’ondes des orientation concernées. La valeur totale de l’astigmatisme est calculée (notée « Magnitude »).
– Les valeurs X astig et Y astig sont reportées sur le graphiques. Il est rappelé que, par convention, les axes des termes de Zernique X astig et Y astig forment un angle de 45°. Ces coordonnées sont représentées par des points dont la légende associe la couleur à l’orientation correspondante. Les points associés aux paires de mesures décalées de 90° sont reliés deux à deux par des segments. Généralement ils doivent être parallèles entre eux pour les paires 0° / 90° et 180° / 270° et perpendiculaires avec les paires 45° / 135° et 225° / 315°. Si ce n’est pas le cas, on pourra soupçonner une anomalie. Le meilleur cercle passant par ces points est calculé puis tracé en vert sur le graphique. Les coordonnées X astig et Y astig du centre de ce cercle sont notées « Mean » dans le tableau et représentent les valeurs d’astigmatisme du front d’onde « moyen » des différentes orientations. Ces valeurs ne sont donc pas une simple moyenne arithmétique des valeurs de chaque orientation mais elles ne s’en écartent généralement que de peu. Si ce n’est pas le cas, on peut également soupçonner une anomalie.
– Les croix colorées sur le graphique représentent les valeurs X astig et Y astig des fronts d’ondes  des défauts induits par le support pour chaque orientation. La moyenne de ces valeurs est représentée par une étoile noire sur le graphique.
– L’erreur standard (Notée STD : « Standard deviation » en anglais) est calculée par rapport à cette valeur moyenne. Elle permet de juger de la validité de l’analyse des effets induits du support. Dans l’exemple traité ici, on pourrait représenter cette valeur par le cercle rouge ci-dessous (rayon = STD) :

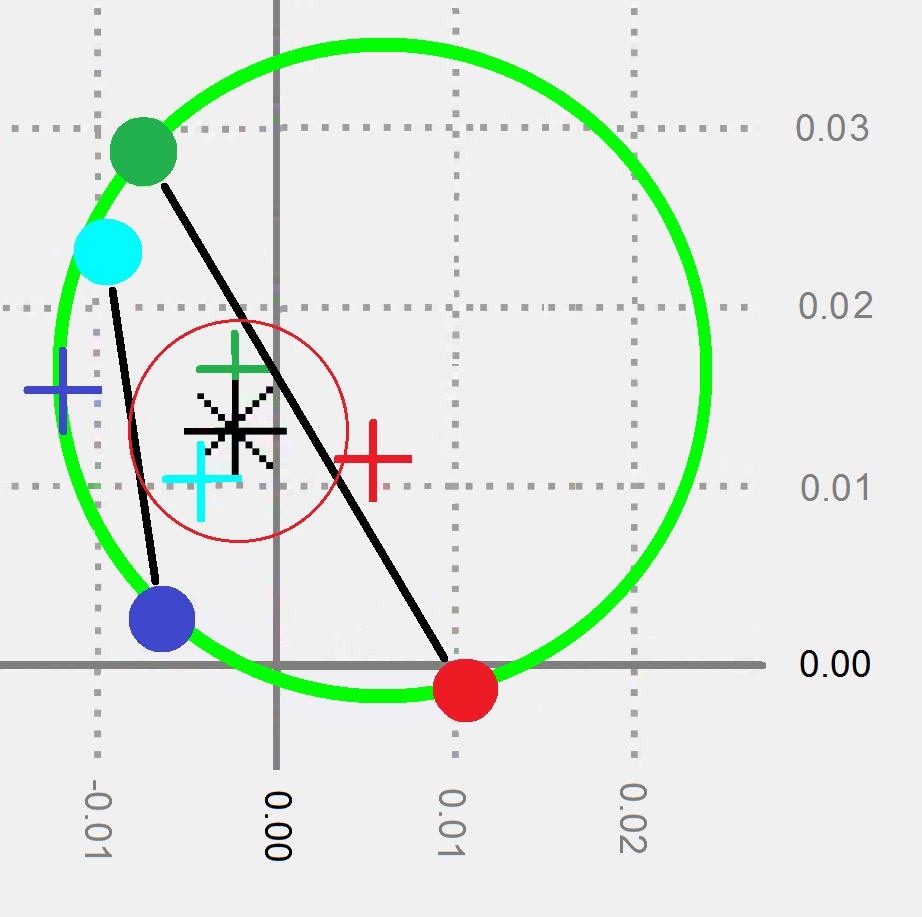
Ces différents calculs et représentations permettent de vérifier la relative reproductibilité des défauts d’astigmatisme induits par le support aux différentes orientations du miroir, condition nécessaire à la validation du calcul final du front d’onde moyen noté « Averaged surface with stand induced terms removed ». Pour ce faire, on contrôlera que les critères suivants sont vérifiés :

• Les points colorés doivent se trouver au plus près du cercle vert
• Les lignes joignant les paires de points colorés doivent être approximativement parallèles entre elles si elles sont décalées de 90° ou perpendiculaires si elle sont décalées de 45°.
• La forme des fronts d’ondes induits par les défauts du support de contrôle pour chaque orientation doit être similaire.
• La grande étoile noire doit être au plus proche du centre du cercle vert.
• L’erreur standard (STD) doit être inférieure à 0,1 (soit 1/10ème de longueur d’onde PTV).

Une fois validé selon les critères ci-dessus, le front d’onde moyen des défauts induits par le support de contrôle pourra être utilisé au besoin pour le soustraire à des fronts d’ondes correspondant à une seule orientation pour exploiter des résultats sans passer par une moyenne de plusieurs orientations.

 

Flou Gaussien :

Malgré un grand nombre de fronts d’ondes moyennés sur plusieurs orientations, certains défauts résiduels apparaissent encore sur le front d’onde final. Ces déformations, généralement de haute fréquence, sont les restes d’artefacts ou de bruit que le logiciel n’a pu traiter complètement (voir exemple ci-dessous).

Le logiciel dispose d’un outil performant qui permet de nettoyer ces dernières scories : Il s’agit du flou gaussien bien connu des astrophotographes amateurs. Pour appliquer ce traitement de la façon la plus objective possible, encore faut-il faire la part des défauts virtuels (artefacts, bruit, …) des défauts réels. Pour cela, Dale Eason (concepteur du logiciel) propose une méthode particulièrement pertinente :

Il préconise d’utiliser la modélisation virtuelle d’un Foucaulgramme à l’aide du logiciel et de la comparer à un Foucaulgramme réel du miroir puis de jouer sur le réglage du filtre Gaussien jusqu’à obtenir un aspect comparable. On accède à la modélisation Foucault en sélectionnant l’onglet « Ronchi Foucault » :

On peut modifier la zone « coupée » en jouant sur les valeurs des champs « Roc Offset » et « Latéral Offset ». Il est parfois nécessaire de cliquer sur « recompute » ou de changer d’onglet pour rafraîchir l’image.

Dans l’exemple ci-dessous, le foucaulgramme virtuel de départ (vue de gauche) présente un mammelonnage qu’on ne retrouve pas dans le foucaulgramme réel (vue du centre). En ajustant le diamètre du filtre Gaussien, on obtient un nouveau foucaultgramme (vue de droite) dont la douceur de la forme est plus fidèle à la réalité. La vue 3D du front d’onde s’en trouve également lissée.

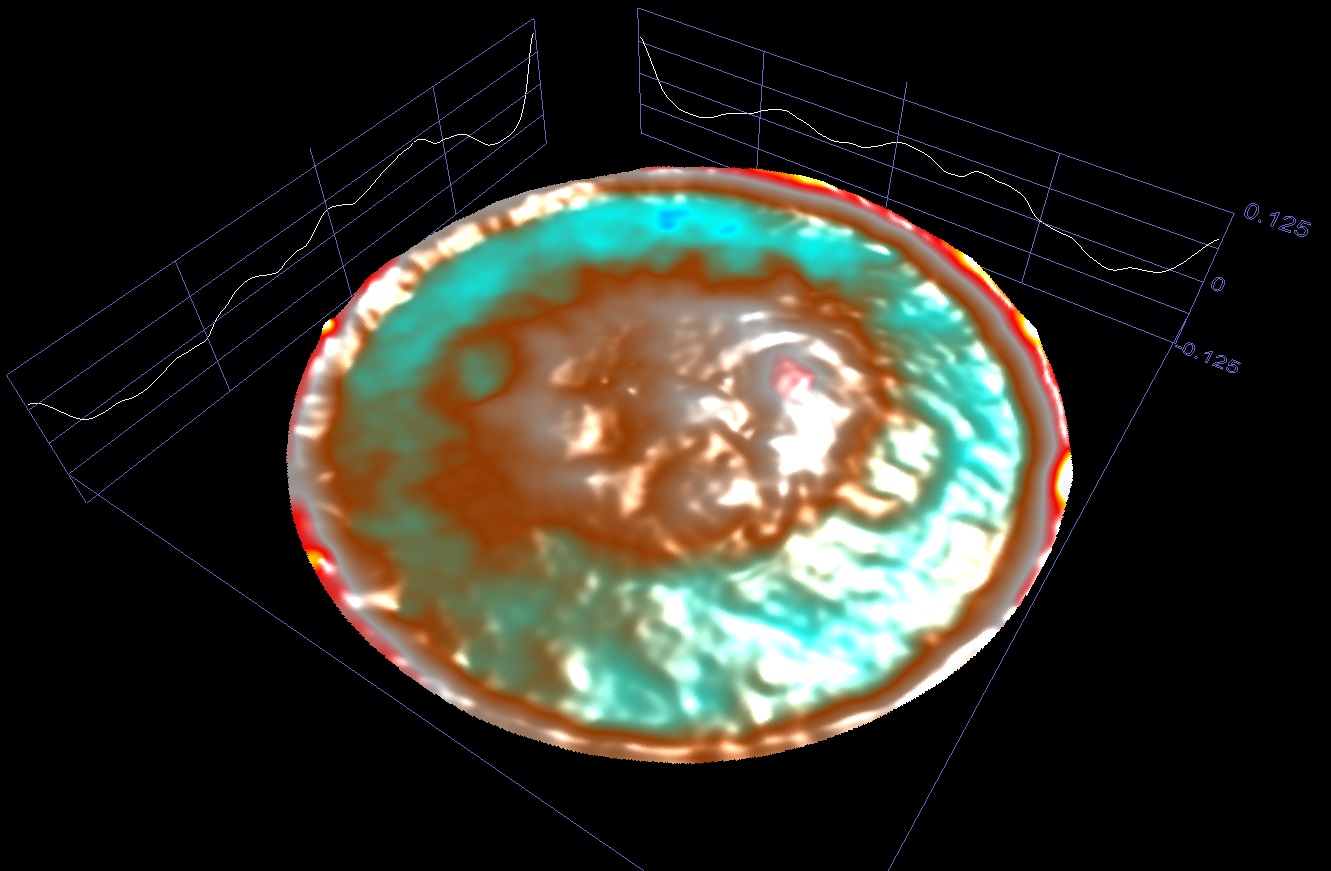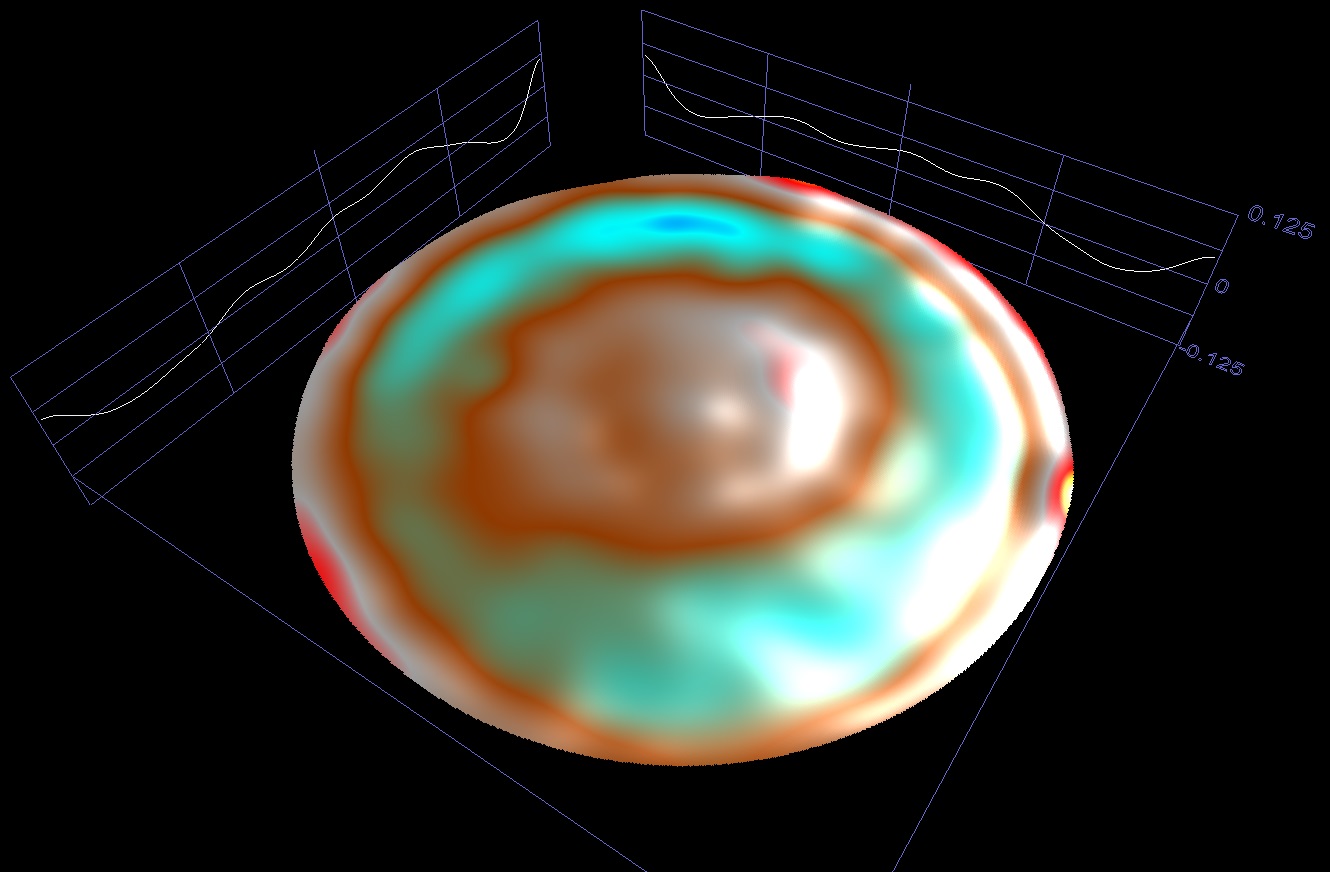Dans les cas courants, une valeur de 20% semble satisfaisante pour le diamètre du masque flou. Il est à noter que ce traitement peut générer un léger effet de bord qu’il faut surveiller. Enfin, on signalera que ces valeurs ne sont pas sauvegardées avec le front d’onde.

 

Édition du rapport :

Le logiciel permet l’édition d’un rapport de contrôle complet via le menu « Files / Save PDF report ». Une boite de dialogue permet de sélectionner certaines rubriques que l’on souhaite éditer dans le rapport.

 

Quelques fonctions avancées :

Neutralisation de zones :

Il est possible de définir une portion de l’interférogramme que l’on souhaite exclure lors du calcul du front d’onde. Cette fonction peut s’avérer utile dans certains cas :

• Présence d’une patte de maintien visible dans le périmètre de l’interférogramme
• Présence d’un œillet au centre du miroir
• Présence d’éclats de verre sur la surface optique
• Artefacts difficiles à neutraliser (liés à la présence de poussières par exemple)
• Franges circulaires impossibles à « évacuer » (dans le cas de grands miroirs ouverts par exemple).

Il faudra toutefois s’assurer que cette cette manipulation ne conduira pas à effacer des défauts réels significatifs. L’analyse des différents interférogrammes selon plusieurs orientations de franges et du miroir y contribuera.

Dans l’onglet « Interferogram tools », on sélectionne l’option « Region ». On a alors le choix entre un tracé libre (« Free form ») ou une forme à base de lignes droites (« Line »).

Il suffit alors de définir le contour de la région à exclure avec le pointeur (Cliquer/glisser pour la forme libre, plusieurs clics pour les lignes). Le logiciel affecte une référence à chaque région qu’il est possible d’effacer si l’on n’est pas satisfait du tracé (bouton « Delete »).

 

Histogramme des erreurs d’un front d’onde :

A partir de l’onglet « Results », on peut cliquer sur le bouton « Histogram »

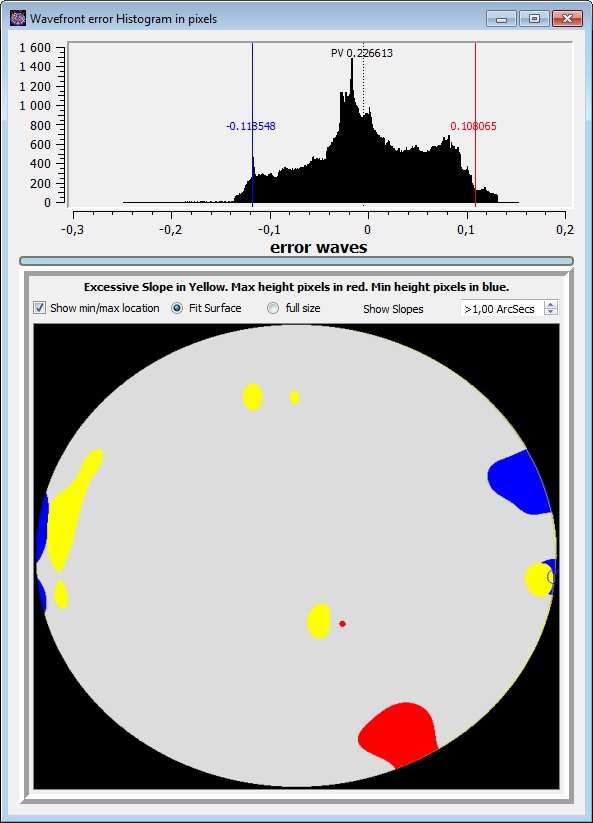
L’histogramme en partie haute représente le nombre de pixels par tranches de valeurs PTV. Des lignes verticales représentent les seuils mini (bleu) et maxi (rouge) dont il est possible de modifier les positions par un cliquer/glisser. L’écart PTV entre ces deux seuils apparaît entre les deux lignes. Dans la figure du bas, on voit alors se teinter en bleu et en rouge les zones du miroir respectivement inférieures et supérieures à ces seuils. Cette représentation permet de visualiser clairement l’étendue des zones dépassant ces seuils et donc de leur contribution plus ou moins importante à la dégradation de la figure de diffraction.

On peut également visualiser les zones (en jaune) dont les pentes dépassent une valeur prédéfinie (en sec d’arc). Par ce moyen, on repérera facilement les zones du front d’onde à l’aberration transversale la plus élevée et qui contribuent plus particulièrement à la dégradation de la valeur du rapport de Strehl.

 

Comparaison de plusieurs profils et fronts d’ondes :

Il est possible de superposer les profils de plusieurs fronts d’ondes sur le même graphique. En cochant la case « All wave fronts » on voit apparaître les profils de tous les fronts d’ondes ouverts. L’orientation de la coupe peut être modifiée avec le cadrant.

Cette visualisation est pratique pour juger de l’homogénéité des fronts d’ondes et des variations de l’astigmatisme.

En cliquant sur le bouton, « Show All Wavefronts », on peut visualiser les cartes de contours de tous les fronts d’ondes ouverts :

On peut ainsi mieux visualiser les variations éventuelles de forme dans le temps (par exemple celles liées à la flexion du miroir ou à la turbulence) ou vérifier qu’un défaut d’astigmatisme tourne avec l’orientation du miroir.

 

Statistiques de fronts d’ondes :

Ces statistiques sont accessibles via le menu «View / Show Statistics of Loaded wavefronts » :

Le graphique du haut permet de visualiser les variations des valeurs RMS (courbe bleue) et Strehl (points rouges) des différents fronts d’ondes ouverts. Cela permet notamment de vérifier l’homogénéité relative des résultats et, dans le cas contraire, d’en tirer des enseignements pour identifier et corriger le problème.

Le graphique du bas, quant à lui, détaille les valeurs RMS pour chaque terme du polynôme de Zernike. Cette visualisation renseigne ainsi facilement sur :

• Quel(s) défauts est(sont) le(s) plus gros contributeur(s) à la valeur RMS globale
• L’amplitude des variations propre à chaque défaut (terme)

En cochant la case « zerns from x to x » on peut faire apparaître la courbe propre à chaque terme dans le graphique du haut.

 

Statistiques sur l’astigmatisme :

Cette analyse est accessible via le menu « Tools / astig Stats » :

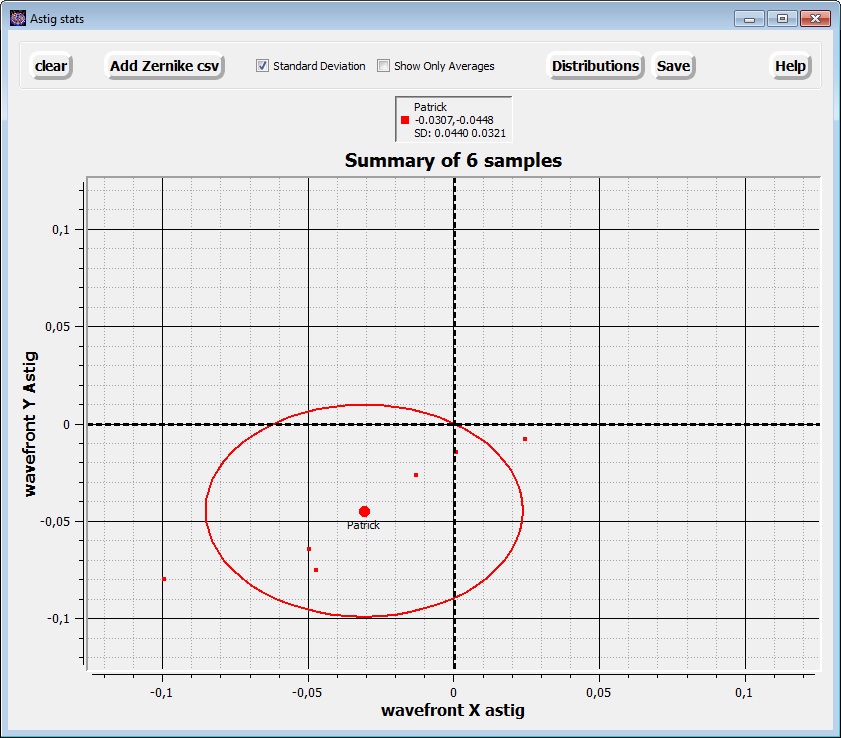
Le graphique réalise un nuage de points à partir des valeurs des termes Wyant « XAstig » et « YAstig » de tous les fronts d’ondes ouverts. La valeur moyenne est repérée par un point plus gros. Cette visualisation permet de mettre en évidence l’évolution de l’amplitude et de la direction (X et Y) du défaut. Le front d’onde concerné par chaque point apparaît en survolant celui-ci. Pour que cette analyse ait un sens, il convient d’intégrer un échantillon suffisant de mesures. Un regroupement des points dans une zone restreinte témoignera d’une stabilité des mesures pour une même orientation du miroir et donc d’une certaine fiabilité des mesures. On peut faire apparaître un cercle centré sur la moyenne et matérialisant l’écart type des mesures en cochant la case « Deviation ». Cet outil est notamment bien adapté à la mise en évidence de la turbulence dont l’effet le plus sensible impacte principalement le défaut d’astigmatisme. Il permet également d’évaluer l’influence d’un éventuel astigmatisme lié au support de contrôle.

 

Soustraction de fronts d’ondes :

Il peut être intéressant de soustraire deux fronts d’ondes afin de localiser et quantifier les défauts résiduels qui expliquent la différence de forme et de précision entre les deux. Pour ce faire, on sélectionne un premier front d’onde dans la liste de l’onglet « Surface ». On active ensuite le menu « Tools / Subtract wave front ». Une boite de dialogue propose alors de sélectionner le front d’onde à retrancher au premier parmi la liste de ceux ouverts. La validation entraîne le calcul d’un nouveau front d’onde représentant le résiduel des deux précédents. Cette fonction peut s’avérer utile pour visualiser la variation de forme du front d’onde entre deux orientations du miroir ou pour mettre en évidence les différentiels de fronts d’ondes issus d’appareils de mesures différents.

 

Paramétrage d’apparences :

Il est possible de modifier l’apparence de la vue 3D des fronts d’ondes via le menu « View / Lighting properties » ou directement depuis le graphique en cliquant sur le bouton « Lighting » :

On a ainsi le choix entre différents rendus de matériaux et l’on peut régler les niveaux de luminosité, de diffusion, …

On peut également modifier l’échelle chromatique via le menu « Tools / User Color Map ».

 

Modélisation d’interférogrammes et de fronts d’ondes artificiels :

Le logiciel dispose d’un outil de création d’interférogrammes et de fronts d’ondes artificiels particulièrement puissant et utile en pratique. On l’active via le menu « Simulations » :

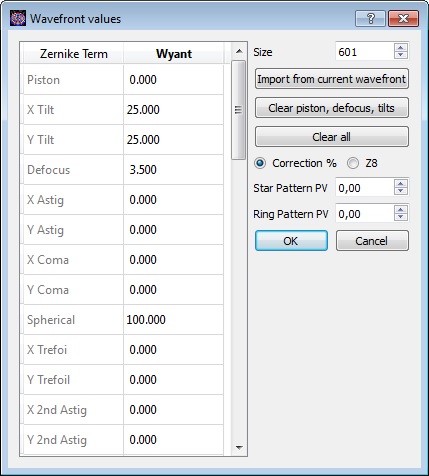
Le tableau des termes du polynôme de Zernike autorise la saisie de valeurs « Wyant » (défaut PTV) au choix de l’utilisateur. Dans le cas d’un miroir asphérique, il faudra tenir compte de l’aberration sphérique au centre de courbure. Pour la compenser, on a le choix entre deux options :

• Cocher l’option « Z8 » puis saisir la valeur Wyant du terme « Spherical » correspondant au calcul « Artificial Null » récupérable dans la boite de dialogue « Mirror configuration ».
• Cocher « Correction % »  puis saisir 100% pour la valeur Wyant de « Spherical ».

On saisit ensuite les valeurs de défauts que l’on souhaite introduire dans le front d’onde. On ajuste par-ailleurs les valeurs optimales de defocus et tilt en X et Y.

Cet outil sera d’une aide précieuse pour optimiser le positionnement initial de l’interféromètre. En effet, on pourra rechercher l’aspect idéal des franges en jouant sur les valeurs de defocus et tilt X et Y. On disposera  ainsi d’une référence à comparer aux interférogrammes successifs lors des phases de réglages.

 

Calibrage objectif photo :

Comme évoqué plus haut, les éventuels défauts de distorsion des objectifs photographiques peuvent dans certains cas suffisamment déformer les images d’interférogrammes pour altérer la précision des résultats. Certains sites sur le Web présentent des tests optiques de nombreux objectifs permettant d’évaluer son propre matériel (voir chapitre “Ressources” ci-dessous). A défaut, le logiciel DFTFringe permet de calibrer la distorsion de l’objectif utilisé à partir d’un cliché d’une trame de référence. Les résultats de ce calcul peuvent alors être enregistrés puis utilisés pour corriger automatiquement des images d’interférogrammes. L’aide associée à cette fonction décrit en détail le mode opératoire.

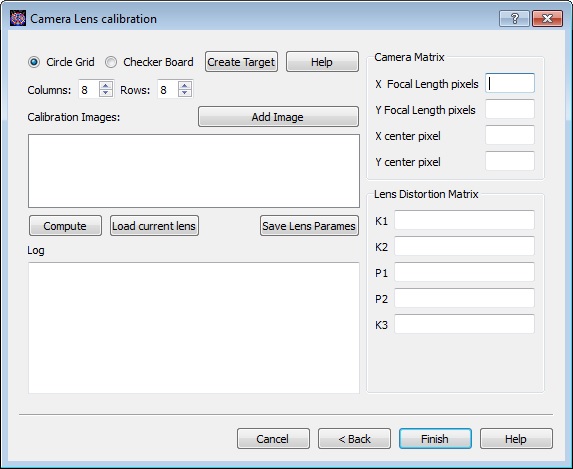	Exemple d’un résultat de test de distorsion sur un zoom Canon EF-S 18-55 (source Optical Limits)

–

 

 

 

Ressources :

 

Forums / Groupes de discussions :

• Interferometry: Ce groupe, initié par Dale Eason (concepteur du logiciel DFTFringe), est une mine d’informations pour l’utilisateur souhaitant s’initier ou se perfectionner dans cette discipline. On y trouve notamment une section Wiki particulièrement riche. Les échanges y sont particulièrement riches et denses.
• Astrotreff: Forum allemand avec une section consacrée à l’optique avec des échanges fréquents sur l’interférométrie amateur particulièrement en pointe dans ce pays.
• Cloudy Nights: Forum américain dans lequel il est régulièrement question d’interférométrie amateur dans sa section optique. Dale Eason y intervient parfois.

 

Sites de référence :

• Charles Rydel: Un site de référence de la part de l’auteur ayant largement contribué à la démocratisation de l’interférométrie dans le milieu amateur français. On signalera particulièrement deux articles parus dans la revue L’Astronomie.
• Airylab : Frédéric Jabet consacre quelques rubriques de sa section « Optimédia » aux moyens de contrôle et notamment l’interférométrie. Très pédagogiques, ces pages sont à recommander.
• Astro-foren: Site allemand de Wolfgang Rohr dans lequel il vulgarise abondamment l’interférométrie. Il y publie également des tests qu’il réalise lui-même dans un cadre professionnel.
• University of Arizona : Page du site dédiées à l’optique de l’université dans laquelle professe James C. Wyant qui a donné son nom à des termes du polynôme de Zernike.
• Amateur Telescope Optics: Un site très complet sur les notions d’optique astronomique et notamment l’interférométrie.

 

Documents :

• Karl-Ludwig Bath: Article original paru dans la revue « Sterne und weltraum » en 1973 (traduction en anglais)
• Les Polynômes de Zernike: Dans ce document, Pierre Strock aborde de manière complète et pédagogique les notions relatives aux polynomes de Zernike utilisés notamment par le logiciel DFTFringe.
• Interferometry and Telescopes : Un guide pour construire et utiliser son propre interféromètre par Peter Ceravolo.
• Using The Ross Null Test : Un guide pour comprendre les différentes méthodes de compensation de l’aberration sphérique au centre de courbure d’un miroir.

 

Vidéos :

• Dale Eason Channel: Plusieurs vidéos sur l’utilisation de fonctions de DFTFringe
• Dale Eason: Réglage de l’interféromètre
• Ed Jones: Fabriquer un interféromètre de Bath
• Ed Jones: Utiliser un interféromètre de Bath
• Régler l’interféromètre de Bath – Partie 1
• Régler l’interféromètre de Bath – Partie 2

 

Ouvrages :

• Conception et constructions de télescopes et astrographes d’amateur : Éditions de boeck, sous la direction de Charles Rydel. Certains chapitres sont consacrés à l’interféromètre de Bath (utilisation, logiciel d’analyse, comparatif avec des méthodes de contrôle professionnelles, …).
• Interferometry for Amateur Telescope Makers : Éditions Willmann-Bell, William Zmek
• Optical shop testing : Éditions Wiley, Daniel Malacara

 

Logiciels :

• DFTFringe: Site de téléchargement de ce merveilleux logiciel. Il est le successeur du logiciel OpenFringe qui n’est plus mis à jour et qui est, de ce fait, moins performant.
• DigiCamControl: Logiciel de contrôle à distance d’un APN Canon ou Nikon.

 

Fournisseurs :

• Surplus Shed : Fournisseur américain de nombreux composants optiques à bas prix particulièrement adaptés à la fabrication d’un interféromètre amateur.
• Edmund Optics : Fournisseur de composants optiques de qualité mais avec un prix en conséquence.
• Melles Griot : Même catégorie de fournisseur qu’Edmund Optics.
• Picotronic: Fournisseur de modules laser de qualité (large gamme)
• Roithner Lasertechnik : Même type de fournisseur que Picotronic

 

Divers :

•  Optical Limits: Site publiant de nombreux tests d’objectifs photo. Les défauts de distorsion y sont notamment calibrés.

---

Dernière mise à jour le 21 janvier 2020

---