Le système solaire

Le système solaire à travers les âges

Le modèle antique de l’Univers a été difficilement remplacé à partir de la Renaissance

La contribution apportée par les philosophes et les scientifiques antiques au modèle du système solaire reposait sur des idées élaborées à cette époque, qui se basaient assez peu sur l’observation mais plutôt sur des « à priori » philosophiques voire même religieux.

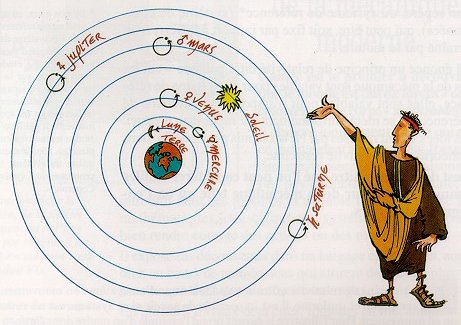Il est cependant surprenant de constater que le modèle de Ptolémée (II° siècle après notre ère) est resté en vogue jusqu’à la Renaissance. Durant le Moyen Age, on continue d’affirmer que les astres circulent dans le ciel sur des sphères cristallines. Jupiter, par exemple, tourne autour de la Terre accompagnée par les anges des hautes sphères. Dieu, Lui, réside au-delà de la sphère cristalline des étoiles. L’enfer est placé dans les entrailles de la Terre cependant que le purgatoire se situe entre la Terre et la Lune. Les âmes impures doivent y faire un séjour plus ou moins prolongé avant de pouvoir accéder aux plus hautes sphères et s’approcher de Dieu. Ce n’est qu’à partir de la Renaissance que certains scientifiques ont osé, souvent au péril de leur vie, remettre en cause ces conceptions.

L’astronomie moderne est née avec le polonais Nicolas Copernic (1473-1543). Après des études à Cracovie, il subit l’influence de la Renaissance italienne par des études complémentaires qu’il accomplit à Bologne (1496), à Rome (1500) et à Padoue (1503). Il rejoint alors la Pologne où il est élu chanoine de Frauenburg. En 1543, après de nombreuses hésitations, il publie le fameux « De Revolutionibus Orbium Coelestium » dans lequel il argumente en faveur d’un univers centré sur le Soleil, la Terre tournant, comme toute autre planète, d’un mouvement circulaire autour de l’astre central. La publication de cet ouvrage reste un des grands jalons de la Renaissance.

Le préfacier de cette œuvre précisait que ce qui y était expliqué n’était qu’une « hypothèse mathématique commode » qui ne décrit pas les mouvements réels des astres mais qui permet seulement de les prévoir. Cette précaution permit que l’Église catholique restât longtemps indifférente aux théories développées par Copernic.

Luther et Calvin, par contre, virent très tôt quel danger elles représentaient par leur contradiction des textes de la Bible : c’était un sacrilège et un blasphème que d’assurer que le Soleil était immobile alors que la Bible relate comment l’Éternel arrêta le Soleil pour aider Josué à triompher de ses ennemis. Or, si Dieu a arrêté le Soleil, c’est que celui-ci bouge. Giordano Bruno, moine défenseur de l’héliocentrisme, qui refusa d’abjurer lors de son procès devant l’Inquisition fut brûlé vif en 1600 sur le Campo de’ Fiori à Rome.

Le « De Revolutionibus orbium coelestium » de Copernic fut mis à l’index en 1616.

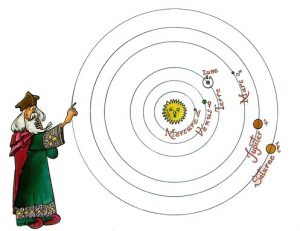
Johan Kepler (1571-1630) naît dans une époque déjà largement influencée par le vent nouveau. Les idées de Copernic ont fait du chemin et sont maintenant largement répandues dans le monde scientifique. Il était l’élève de Tycho Brahé (1546-1601), astronome danois auquel on doit un grand nombre de mesures très précises de la position des astres. C’est principalement en travaillant sur les relevés faits par son maître que Kepler découvrit les lois qui portent son nom.

  Kepler montre que le comportement de l’univers obéit à des lois mathématiques

1 – LOI DES ORBITES

L’orbite de chaque planète est une ellipse, dont l’un des foyers est occupé par le soleil

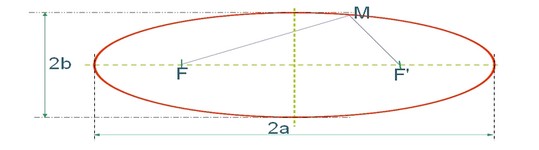
MF + MF’ = Constante

———————————————————

2 – LOI DES AIRES

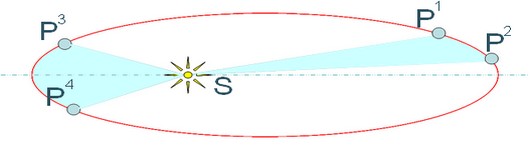
Le mouvement de chaque planète est tel que le segment de droite reliant le soleil et la planète balaie des aires égales pendant des durées égales

 

———————————————————–

3 – LOI DES PÉRIODES

Pour toutes les planètes, le rapport entre le cube du demi grand axe de la trajectoire et le carré de la période est le même.

Cette constante est indépendante de la masse de la planète

Cette loi s’exprime d’une manière plus aisée sous la forme mathématique :

 

Un autre héritier de Copernic : Galilée (1564-1642)

Selon Galilée « le livre du monde est écrit en mathématiques »

Avec lui va prendre vigueur l’astronomie d’observation. Le Moyen-Age et le début de la Renaissance restent très attachés aux idées des astronomes antiques; les conceptions de Ptolémée et d’Aristote sont encore toutes puissantes. Perfectionnant une invention hollandaise, Galilée invente la lunette astronomique qu’il braque vers la Lune, le Soleil, les planètes et les étoiles. Il fait d’emblée un grand nombre de découvertes qui lui permettent de rejeter définitivement les conceptions antiques. Il découvre les satellites de Jupiter, les phases de Vénus, l’anneau de Saturne, les montagnes sur la Lune, les taches solaires, …

 

Galilée découvre les 4 gros satellites de Jupiter et note leurs positions

Selon Galilée, « le livre du monde est écrit en mathématiques ». Cela signifie que les mathématiques permettent de décrire le comportement de la nature. Galilée avait mis cette idée en pratique lors de l’étude du mouvement accéléré. Les conclusions de ses travaux peuvent être exprimées dans le langage mathématique. Ce sont les fameuses formules qui expriment le mouvement rectiligne uniformément accéléré, par exemple. A partir de ce moment, l’usage de l’outil mathématique devient obligatoire en cosmologie.

Dans son « Dialogo », publié en 1632, il s’affirme nettement en faveur des idées de Copernic et de Kepler. Cela lui vaut d’être soumis à l’Inquisition. Il doit à sa renommée (et à son amitié avec le Pape) la chance de ne pas monter sur le bûcher comme le moine Giordano Bruno. Il est cependant obligé d’abjurer en public dans la cathédrale Saint-Pierre à Rome. Le fameux « … et pourtant elle tourne !  (Eppur si muove) », soit disant prononcé après l’abjuration n’est qu’une légende propre à rehausser l’image du scientifique génial et incompris.

Le retentissement du procès de Galilée est tel que le grand philosophe Descartes, réfugié en Hollande, renonce à publier « Le traité du monde et de la lumière » qu’il a écrit en 1632 et 1633, dans lequel il exposait les fruits de ses études sur l’univers et son soutien à la vision héliocentrique. Cet ouvrage ne sera publié qu’en 1664, quatorze ans après sa mort.

Newton apporte la théorie qui permet d’expliquer les observations des ses prédécesseurs

Galilée meurt en 1642, année de la naissance d’Isaac Newton (1642-1727). Par des moyens mathématiques (invention du calcul différentiel et intégral avec Leibniz) et en se basant sur les travaux de Kepler et de Galilée, il montre que l’orbite d’un corps soumis à un champ de gravitation doit être une courbe de la famille des coniques.

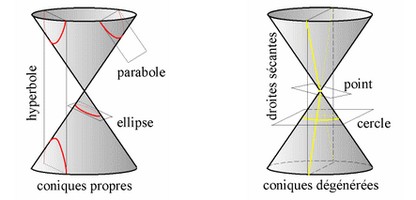
• ellipse (comme le pensait Kepler)
• parabole ou
• hyperbole

 

 

En cela, il enrichit l’apport de Kepler en confirmant de manière théorique (démarche déductive) ce que son prédécesseur avait montré de manière empirique (démarche inductive).

La légende veut que Isaac Newton, fuyant la peste qui sévissait à Cambridge se soit réfugié dans la campagne anglaise. Se reposant à l’ombre d’un pommier, il regardait la Lune lorsqu’il reçut une pomme sur la tête. Bien que cette anecdote soit (plus que probablement) une légende destinée à frapper les esprits, l’analyse de la chute de cette pomme lui aurait valu la révélation de la gravité universelle :

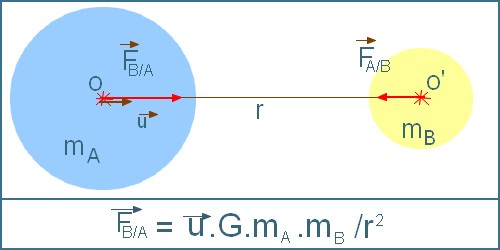
Deux corps quelconques s’attirent en raison directe de leur masse et en raison inverse du carré de la distance de leurs centres de gravité.

Rappelons-nous que la vitesse est une grandeur vectorielle pour bien comprendre la portée de cette loi. Si la vitesse est conservée, elle doit l’être autant en intensité qu’en sens et en direction. Un objet en mouvement sur lequel n’agit aucune force continue de se mouvoir en ligne droite.

Ce principe semble heurter le sens commun puisque nous savons bien que le mouvement perpétuel n’existe pas. Cependant, si tous les mobiles finissent par s’arrêter après une course plus ou moins longue sur la Terre, c’est qu’une force intervient effectivement : la force de frottement.

Dans le « vide » intergalactique, ces forces sont pratiquement inexistantes à cause de la faible densité de matière ; on considérera donc généralement qu’un objet en mouvement y poursuivra son mouvement indéfiniment (cette approximation est fort bonne).

Newton étudie ce principe de manière quantitative : il mesure l’effet de forces d’intensités différentes sur le mouvement sphères qui roulent sur des surfaces planes.

Cette relation mathématique nous enseigne que la force exercée par la Terre sur un satellite est d’autant plus grande que la masse de ce satellite est grande. Il est plus difficile de garder en rotation une boule de plomb de 10 kg accrochée à une corde qu’une balle de tennis accrochée à la même corde. Il est donc bien clair que la force qui retient la Lune près de la Terre est considérablement plus grande que la force qui retient un petit satellite de 100 kg !

D’autre part, la relation nous indique également que la force qui s’exerce dépend d’une certaine manière de la Terre : l’accélération centripète qui est conférée à la lune a une origine terrestre. C’est la même force qui permet à la Terre et aux autres planètes de rester en orbite autour du soleil. Donc, si la Terre exerce une force sur la lune, elle est également l’objet d’une force de la part du soleil. Newton généralise en disant que tout corps est à la fois l’objet et le sujet de la force de gravitation.

Il peut alors démontrer les lois suivantes :

 2 – On me pousse, j’accélère

Une poussée me fait prendre de la vitesse, ou me fait changer de direction ou me fait avancer si j’étais au repos.

Exemple : Une pierre lâchée dans un puits se met à tomber de plus en plus vite sous l’effet de la pesanteur.

3 – Celui qui me pousse, recule

Une poussée vaut à mon pousseur une poussée égale dans l’autre sens. Exemple de la barque qui s’éloigne du bord lorsque, étant dessus, on saute sur la berge.

C’est par l’utilisation du calcul différentiel qu’il a inventé en même temps que Leibniz (1646-1716), que Newton montre que la force qui s’exerce entre deux corps est inversement proportionnelle à la distance qui les sépare (notée R).

Un peu plus tard, le physicien anglais Cavendish (1731-1810) déterminera la valeur de la constante de proportionnalité encore appelée ici constante de gravitation (symbole G) :

G = 6,67.10 -11 m 3/kg s²

Par diverses observations, Newton vérifie que cette loi est valable partout dans l’univers connu ; c’est la raison pour laquelle on parle de la loi de la gravitation universelle pour cette troisième loi de Newton.

 

Affinement des théories durant les Temps Modernes

L’amélioration des moyens d’observation va permettre à l’anglais William Herschel (1738-1822) de découvrir en 1781 la planète Uranus, au-delà de Saturne.

A la fin du XVIII^ème siècle, Titius et Bode découvrent les astéroïdes, ces petites planètes qui gravitent entre Mars et Jupiter. Cette découverte est en grande partie due à l’invention d’une loi purement empirique dont les fondements physiques n’ont été découverts que très récemment. Titius et Bode ont découvert qu’il existait un rapport simple et constant entre les distances qui séparent les planètes du Soleil.

Cette règle fournit approximativement les distances des planètes au soleil exprimées en unités astronomiques. Or, on ne connaissait aucune planète à 2,8 UA du Soleil. L’observation du ciel permit de découvrir, à 2,8 UA non pas une planète, mais des milliers de débris rocheux de tailles diverses : les astéroïdes.

Observant la planète Uranus, le français Le Verrier (1811-1877) décèle des anomalies dans sa trajectoire. Confiant dans les lois de Newton, il prévoit l’existence d’un astre encore inconnu qui perturberait la trajectoire d’Uranus et la rendrait non elliptique. Il calcule la position d’un tel astre hypothétique qui sera observé en 1846 à la position prévue ! On lui donne le nom de Neptune. On découvrira Pluton en 1930, la plus éloignée du Soleil, par le même type de recherches : la théorie de Newton trouve une brillante confirmation. A l’heure actuelle, si l’on n’a pas encore pu mettre en évidence d’autres planètes dans notre système solaire on a, par contre, découvert d’autres corps, notamment dans la nouvelle catégorie (créée en 2006) des planètes naines à laquelle appartiennent désormais Cérès (dans la ceinture d’astéroïdes), Pluton et trois autres objets situés au-delà de Pluton : Hauméa, Makémaké et Éris.

Bientôt, de nouvelles techniques d’observation permettront de faire d’importantes découvertes quant à la structure de l’univers, la nature et la composition des étoiles et des nébuleuses observées depuis très longtemps.

Vous pouvez aussi consulter nos documents pdf :
• Un rapide survol du système solaire (26 pages)
• Le système solaire et au-delà (224 pages)

---