Glossaire astronomique - La saison d'été étant terminée, nous sommes désormais ouverts, sans réservation, tous les vendredis à 21h00.

Ce glossaire sert à expliquer ou compléter des informations sur des mots ou des concepts qu’on peut rencontrer souvent en astronomie. Plusieurs mots ou thèmes seront abordés, faites votre choix ! La liste ci-dessous n’est pas limitative, n’hésitez pas à nous suggérer par e-mail d’autres sujets ou thèmes que vous souhaiteriez voir dans cette liste. D’autres sujets, plus complexes et/ou plus volumineux ne seront pas traités dans ce glossaire. Vous pourrez les trouver généralement dans « nos documents pdf ».

Vous pouvez aller directement à la section qui vous intéresse en cliquant sur l’un des choix ci-dessous. Vous pourrez ensuite revenir directement ici avec la flèche retour de votre navigateur.

1) Albedo
2) Apoapside, Périapside – Aphélie, Périhélie
3) Assistance gravitationnelle
4) Chondrites
5) Distances et unités de distance en astronomie
6) Écliptique
7) Kelvin
8) Kepler (Lois de Kepler)
9) Géocentrisme contre Héliocentrisme
10) Newton (Lois de Newton sur le mouvement et la gravitation)
11) Lagrange (Les points de Lagrange)
12) Libration
13) Nutation
14) Ondes gravitationnelles
15) Phémus
16) Planètes naines et petits corps (dénominations)
17) Précession des équinoxes
18) Quasi-satellites
19) Rotation synchrone (généralement d’un satellite)
20) Saturne : précisions sur les divisions et les “annelets” de la planète
21) Tholins
22) Point vernal, ascension droite, déclinaison, coordonnées équatoriales
23) Aurores polaires
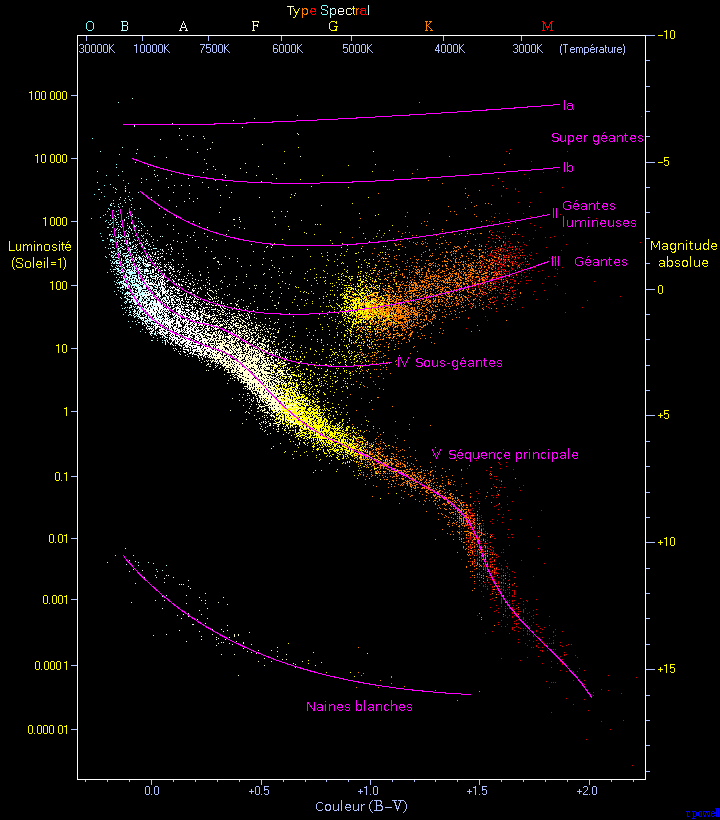
24) Le diagramme de Hertzsprung-Russel
25) Période synodique
26) Lumière cendrée
27) Quasars
28) Pulsars
29) Étoiles à neutrons
30) Les trous noirs
31) Astéroïdes, astéroïdes géocroiseurs, astéroïdes troyens, centaures
32) Analemme
33) Le mouvement rétrograde des planètes
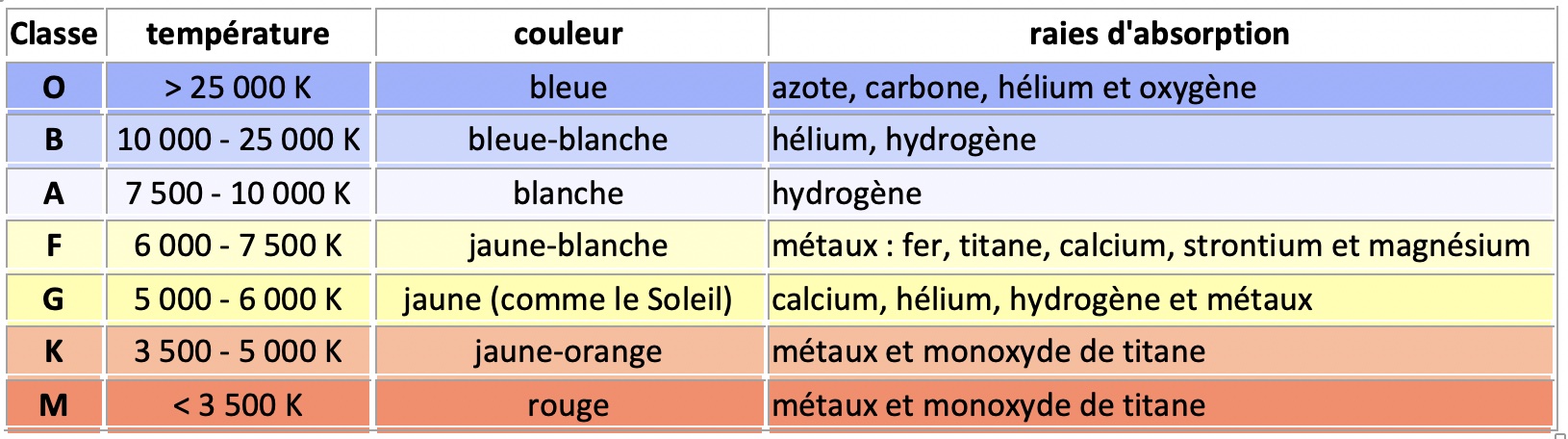
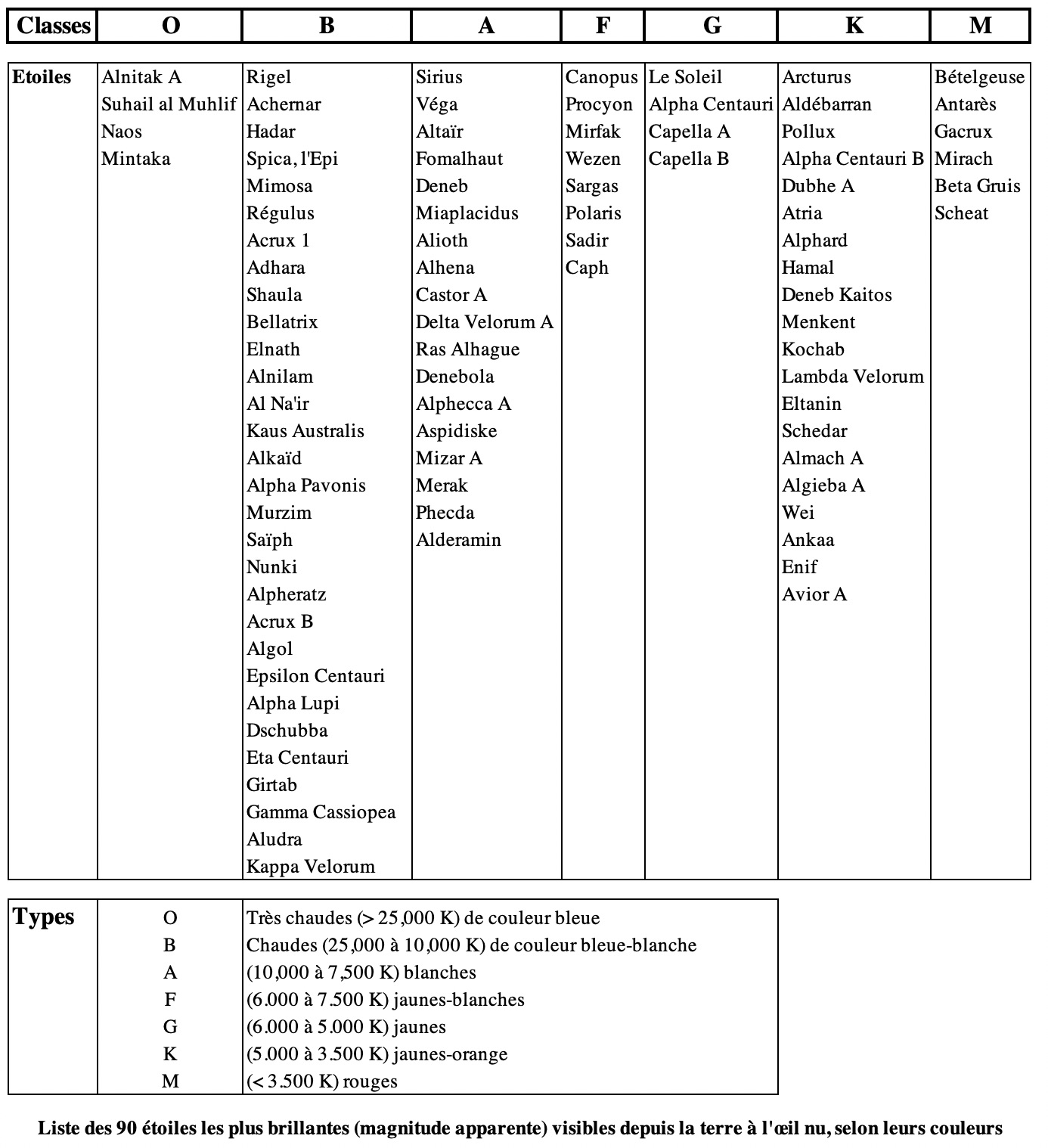
34) Classification des étoiles selon leur couleur (et donc leur température)
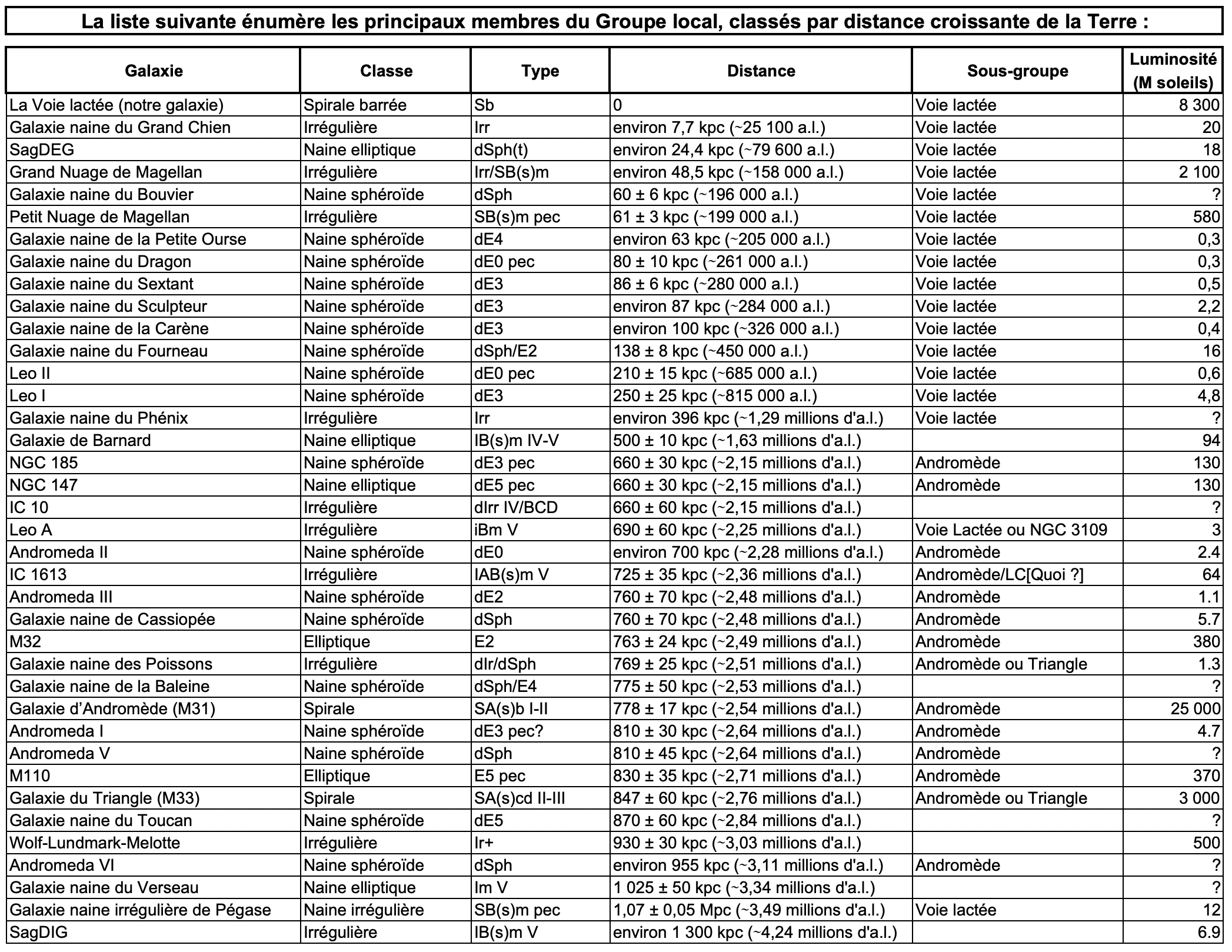
35) Groupes de galaxies, amas, superamas
36) Étoiles filantes, Radiant, Météores, Bolides, etc.
37) Année besselienne
38) Etoiles Wolf-Rayet
39) Globules de Bok
40) Objets Herbig-Haro

–

1) Albedo : L’albédo ou albedo (sans accent), est le pouvoir réfléchissant d’une surface, soit le rapport de l’énergie lumineuse réfléchie à l’énergie lumineuse incidente. C’est une grandeur sans dimension, comparable à la réflectivité, mais d’application plus spécifique, utilisée notamment en astronomie et climatologie ainsi qu’en géologie. Le mot, d’origine latine signifiant blancheur, a été introduit au XVIII^e siècle en optique et en astronomie par le mathématicien et astronome suisse Johann Heinrich Lambert. L’albédo, dans sa définition la plus courante dite albédo de Bond, est une valeur comprise entre 0 et 1 : un corps noir parfait, qui absorberait toutes les longueurs d’onde sans en réfléchir aucune, aurait un albédo nul, tandis qu’un miroir parfait, qui réfléchirait toutes les longueurs d’onde, sans en absorber une seule, aurait un albédo égal à 1. D’autres définitions, dont celle de l’albédo géométrique, peuvent donner des valeurs supérieures à 1.

L’albédo est utilisé en astronomie pour avoir une idée de la composition d’un corps trop froid pour émettre sa propre lumière, en mesurant la réflexion d’une source lumineuse externe, comme le Soleil. On peut différencier ainsi facilement les planètes gazeuses, qui ont un fort albédo, des planètes telluriques qui ont elles, un albédo faible. Les astronomes ont affiné cette définition en distinguant d’une part l’albédo de Bond, correspondant à la réflectivité globale d’un astre pour toutes les longueurs d’onde et tous angles de phase confondus, et d’autre part l’albédo géométrique, correspondant au rapport entre l’intensité électromagnétique réfléchie par un astre à angle de phase nul et l’intensité électromagnétique réfléchie à angle de phase nul par une surface équivalente à réflectance idéalement lambertienne (c’est-à-dire isotrope quel que soit l’angle de phase) : conséquences de ces définitions, l’albédo de Bond est toujours compris entre 0 et 1, tandis que l’albédo géométrique peut être supérieur à 1.

–

2) Apoapside, Périapside – Aphélie, Périhélie

a) Apoapside et périapside :

Un diagramme de Kepler des éléments orbitaux. F est le périapse, H est l’apoapse, la ligne rouge entre eux est la ligne des apsides. ↓

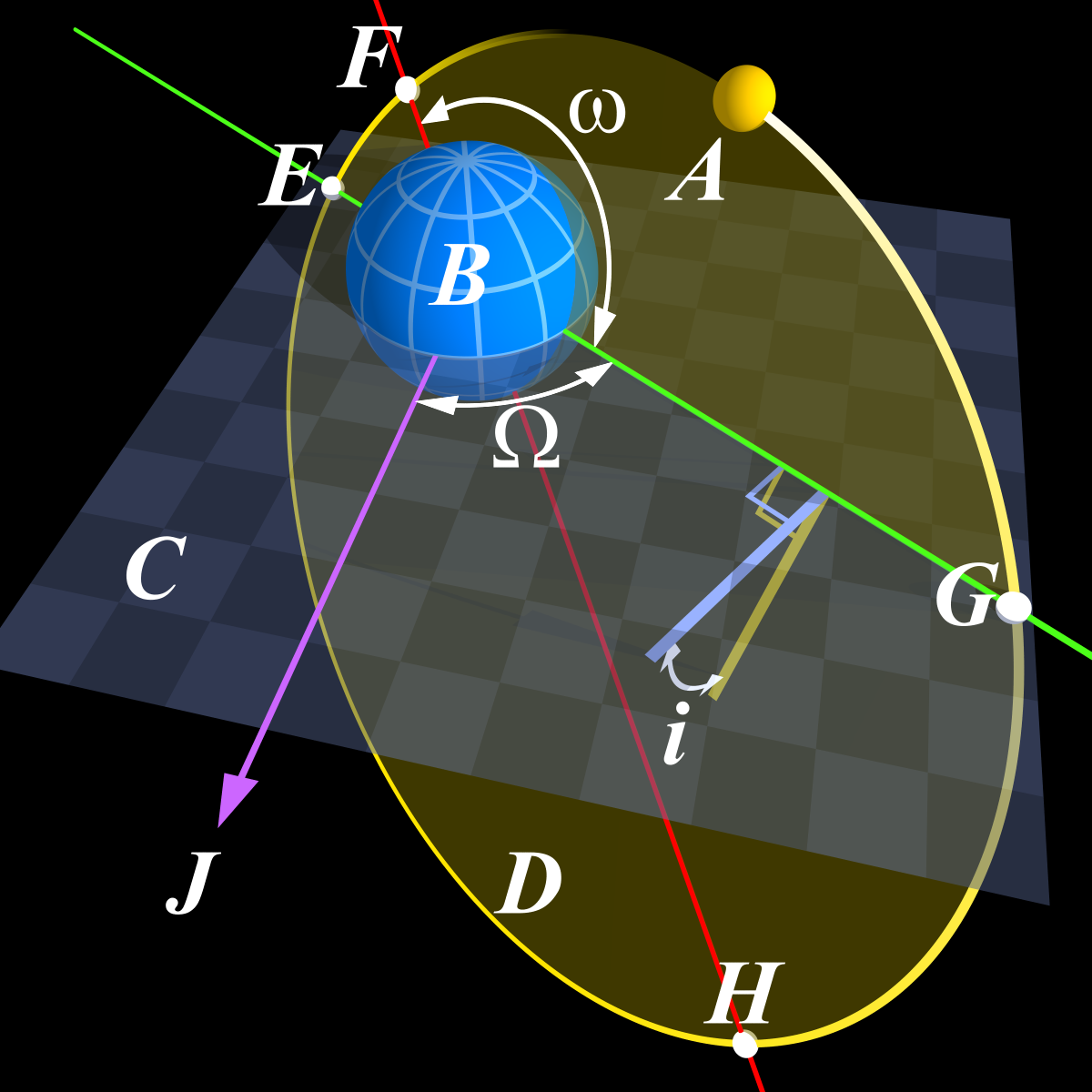L’apoapside, apoapse, apside supérieure ou apocentre est le point de l’orbite d’un objet céleste où la distance est maximale par rapport au foyer de l’orbite (point H sur la figure ci-contre).

Son antonyme est périapside, périapse, ou péricentre (point F sur la figure ci-contre). Ces deux points extrêmes (périapside et apoapside) sont désignés ensemble sous le terme générique de apsides. Attention, le « Foyer » de l’orbite d’un astre n’est généralement pas le centre de l’ellipse de sa révolution autour de son étoile ou de sa planète. On utilise généralement ces termes pour des satellites (naturels ou pas), car dans le cas d’une planète autour de son étoile on parlera d’aphélie et de périhélie (en grec hélios veut dire soleil).

b) Aphélie et périhélie :

Le périhélie est le point de la trajectoire d’un objet céleste en orbite héliocentrique (autour du soleil) qui est le plus proche de l’étoile autour de laquelle il tourne.

L’aphélie est, au contraire, le point de la trajectoire d’un objet céleste en orbite héliocentrique qui est le plus éloigné de l’étoile autour de laquelle il tourne.

On a ci-dessous le schéma simplifié de l’orbite de la Terre autour du Soleil, montrant ces deux points particuliers que sont l’aphélie et le périhélie.

L’ellipticité est volontairement exagérée sur ce schéma, l’orbite de la Terre étant en pratique très proche d’un cercle. En effet, à son périhélie la Terre est à 0,9833 UA du soleil contre 1,0167 UA à l’aphélie, soit 3,2 % de différence de distance.

Le périhélie se situe dans le temps terrestre entre le 2 et le 5 janvier et l’aphélie entre le 3 et le 7 juillet.

Il existe de nombreux mots spécifiques pour qualifier les points les plus près (péri-) et les plus loins (apo-) d’objets en rotation elliptique autour d’autres objets. Exemple, dans le cas d’un objet (par exemple un satellite) en orbite elliptique autour de Neptune, on parlera de “périposéide” au plus près et “d’Apoposéide” au plus loin. Notons que ces mots sont très rarement employés dans la pratique. À titre de curiosité, les voici :

Points les plus proches, préfixe Péri-

Galaxie : Périgalacticon
Trou noir : Périmélasme
Étoile : Périastre
Soleil : Périhélie
Mercure : Périherme
Vénus : Péricythère
Terre : Périgée
Lune : Périsélène
Mars : Périarée
Jupiter : Périzène
Saturne : Périkrone
Uranus : Périourane
Neptune : Périposéide
Pluton : Périhade

Points les plus lointains, préfixe Apo-

Galaxie : Apogalacticon
Trou noir : Apomélasme
Étoile : Apoastre
Soleil : Aphélie
Mercure : Apherme
Vénus : Apocythère
Terre : Apogée
Lune : Aposélène
Mars : Apoarée
Jupiter : Apozène
Saturne : Apokrone
Uranus : Apourane
Neptune : Apoposéide
Pluton : Aphade

NB : Les suffixes correspondent généralement à l’étymologie des noms des dieux grecs associés aux planètes du système solaire.
-Hélie, Helios le Soleil en grec, Sol chez les romains.
-Herme, le dieu grec Hermès, Mercure chez les romains.
-Cythère, lieu de naissance de la déesse grecque Aphrodite, Vénus chez les romains.
– Gée, la Terre chez les grecs (ou Gé ou Gaïa), Tellus chez les romains.
-Arée, Arès le dieu grec de la guerre, Mars chez les romains.
-Zène, vient du dieu grec Zeus, Jupiter chez les romains.
-Krone, du dieu grec Kronos ou Cronos, Saturne chez les romains.
-Ourane, dieu grec Ouranos, Uranus chez les romains.
-Poséide, du dieu grec de la mer, Poséidon, Neptune chez les romains.
-Hade, du dieu grec des enfers Hadès, Pluton chez les romains.

–

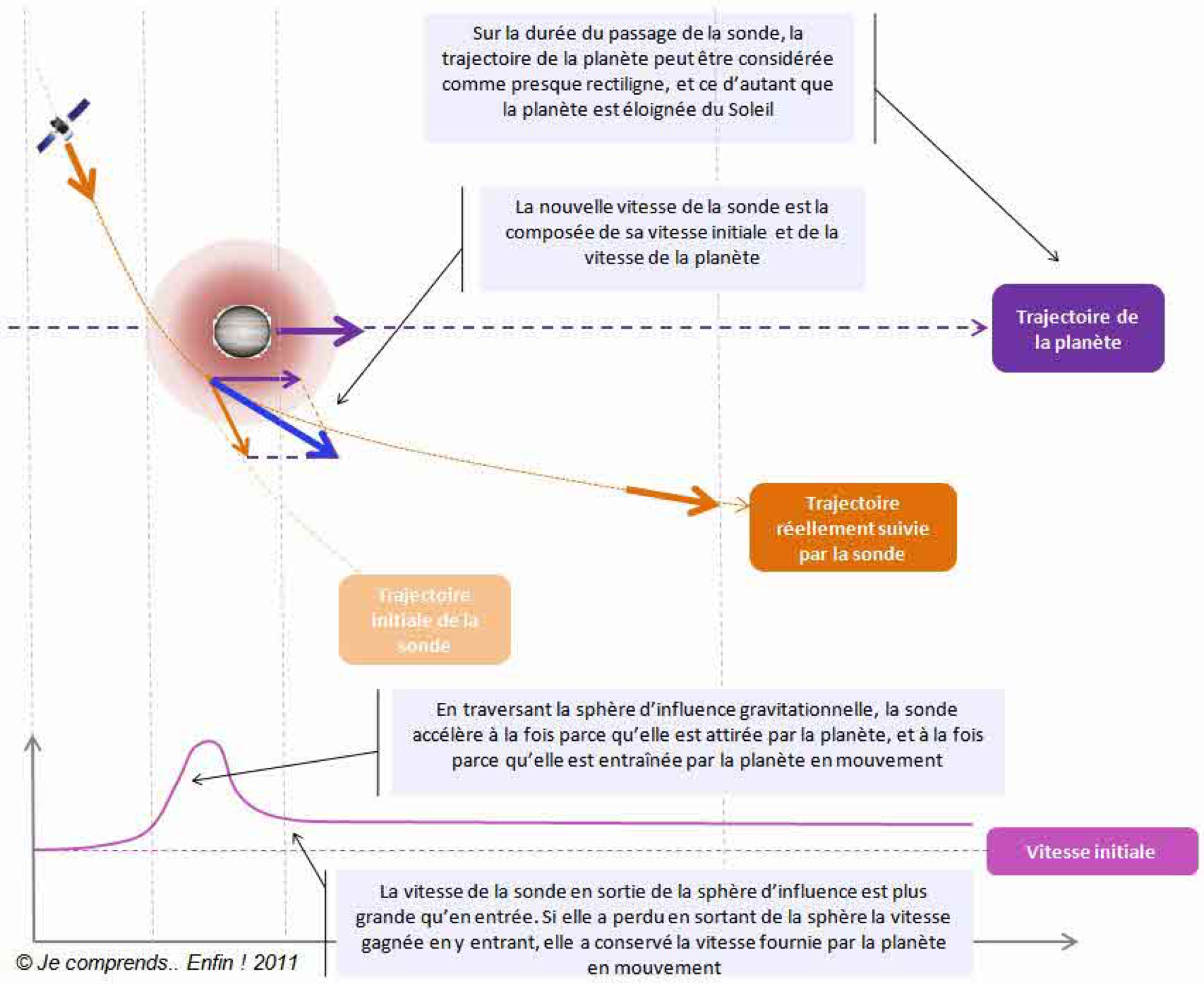
3) Assistance gravitationnelle

Quand on envoie des sondes dans l’espace, notamment vers des planètes plus ou moins lointaines, on est confronté à deux problèmes : la vitesse de déplacement de la sonde qui nous fera arriver plus tôt ou plus tard vers l’objectif choisi et la consommation de carburant.

Les sondes spatiales, une fois lancées dans l’espace n’ont pas besoin de consommer beaucoup de carburant pour avancer car elles sont dans le vide, rien ne les ralentit, elles sont en vol “ballistique”, à vitesse constante. Le principal problème est d’échapper à l’attraction terrestre, puis d’accélérer suffisamment pour atteindre une vitesse suffisante pour réussir la mission. La fusée lanceuse doit faire fonctionner ses moteurs grâce à du carburant. Mais la fusée est généralement énorme (et donc lourde) et elle doit emporter la sonde et beaucoup de carburant pour effectuer des corrections de trajectoire puis, à la fin, pour décélérer et se mettre en orbite autour de la planète cible. Ces grandes quantités de carburant génèrent aussi un surpoids et donc une surconsommation de carburant : c’est un cercle vicieux !

Les ingénieurs de différents pays ont trouvé une astuce qui va permettre d’accélérer la sonde en ne dépensant qu’un minimum de carburant : l’accélération gravitationnelle.

Cette méthode consiste à passer très près d’une planète en arrivant derrière elle dans le sens de son orbite pour bénéficier de l’attraction de la planète (loi de Newton) qui va donner à la sonde une vitesse supplémentaire. On pourrait croire que cette attraction va jouer dans les deux sens et donc s’annuler car la sonde accélère quand elle est derrière la planète et la rattrape, mais elle va être ralentie une fois la planète dépassée, car l’attraction va jouer négativement ! C’est parfaitement exact, ces deux phases s’annulent et le gain serait nul si la planète était immobile ! Mais c’est oublier un troisième facteur qui est la vitesse de la planète elle-même dans sa révolution autour du Soleil; c’est cette vitesse qui va produire l’accélération désirée.

Dans la première phase on aura un total de vitesse sonde + effet de la gravité + vitesse planète. Dans la seconde on aura un total de vitesse sonde – effet de la gravité + vitesse planète. On est donc gagnant. Ce bonus est d’autant plus important que l’on passe le plus près possible de la planète.

Prenons le cas de la sonde Cassini-Huygens, partie le 15/10/1997 de Cap Kennedy, en route vers Saturne. Malgré la puissance de son lanceur, Cassini-Huygens ne peut pas parvenir sur sa seule lancée jusqu’à Saturne. Pour y parvenir, il aurait été nécessaire que la fusée Titan puisse accélérer la sonde spatiale à une vitesse de 15,1 km/s or, compte tenu de la masse de celle-ci, le lanceur n’a pu lui communiquer qu’une vitesse de 12,4 km/s. Les concepteurs de la mission ont donc prévu d’obtenir la vitesse manquante en utilisant l’assistance gravitationnelle de Vénus (deux fois) et de la Terre. Une dernière assistance gravitationnelle de Jupiter est utilisée pour raccourcir la durée du voyage. La sonde spatiale se dirige d’abord vers Vénus. Comme elle se rapproche du Soleil, la vaste parabole de l’antenne grand gain est interposée entre l’astre et le corps de l’engin spatial, pour limiter l’échauffement. Le 27 avril 1998, Cassini frôle la planète en passant à 287 km de la surface, ce qui lui permet d’infléchir sa trajectoire de 70°, accélère de 3,7 km/s (dans le référentiel héliocentrique) et la place sur une orbite dont l’aphélie se situe au-delà de Mars. Le 3 décembre 1998 la propulsion principale est utilisée pour effectuer une importante correction de vitesse (et donc de trajectoire) de 452 m/s, qui ramène la sonde spatiale pour la deuxième fois au-dessus de Vénus, le 24 juin 1999 à 603 km d’altitude. Avec l’accélération obtenue (3,1 km/s dans le référentiel héliocentrique), la sonde spatiale survole la Terre seulement 56 jours plus tard, à une altitude de 1 166 km le 18 août 1999. L’assistance gravitationnelle liée à ce survol procure à son tour une accélération supplémentaire de 4,1 km/s, et porte la vitesse de la sonde spatiale à 19,1 km/s, ce qui lui permet désormais, après avoir encore accéléré au passage de Jupiter, d’atteindre Saturne le 1^er juillet 2004, soit en un peu moins de sept ans.

Déroulement du parcours de la sonde Cassini-Huygens ↓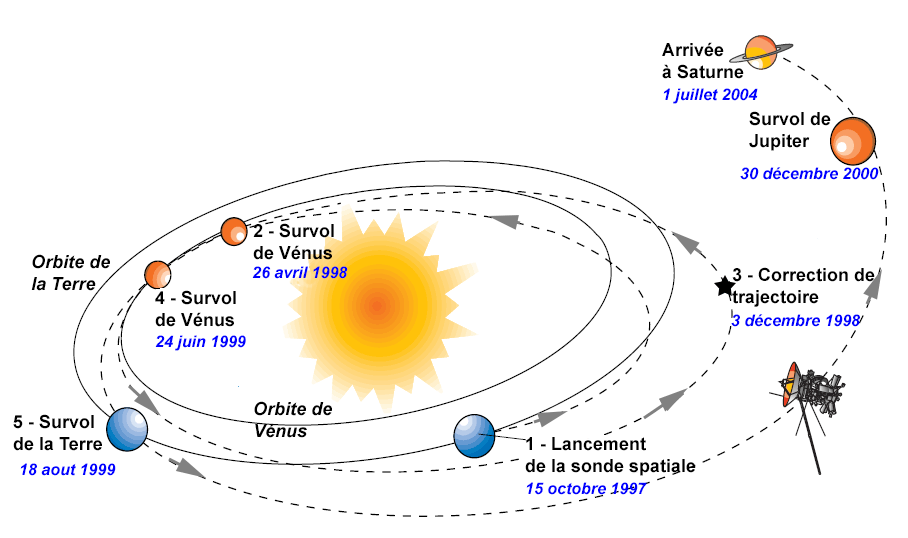

Il faut aussi noter, et c’est très important, que l’assistance gravitationnelle peut aussi servir dans un autre cas : celui où l’on cherche à ralentir une sonde. Les cas les plus connus concernent surtout les sondes envoyées vers les planètes “intérieures”, Vénus et Mercure. En effet, quand on essaie de gagner du temps pour aller vers l’une de ces deux planètes et que l’on veut se mettre en orbite autour de l’une d’elles, il faut très fortement ralentir pour pouvoir le faire. C’est d’autant plus essentiel que l’on se rapproche du Soleil, dont l’influence gravitationnelle devient énorme.

Ici, contrairement à l’accélération où l’on dépasse la planète dans le sens de son mouvement orbital pour bénéficier de sa vitesse propre, on va la prendre “à l’envers”… On ne va pas dépasser la planète, mais la croiser à contre-sens. De cette façon la vitesse de la planète ne s’ajoutera pas à celle de la sonde, mais, au contraire, va se retrancher !

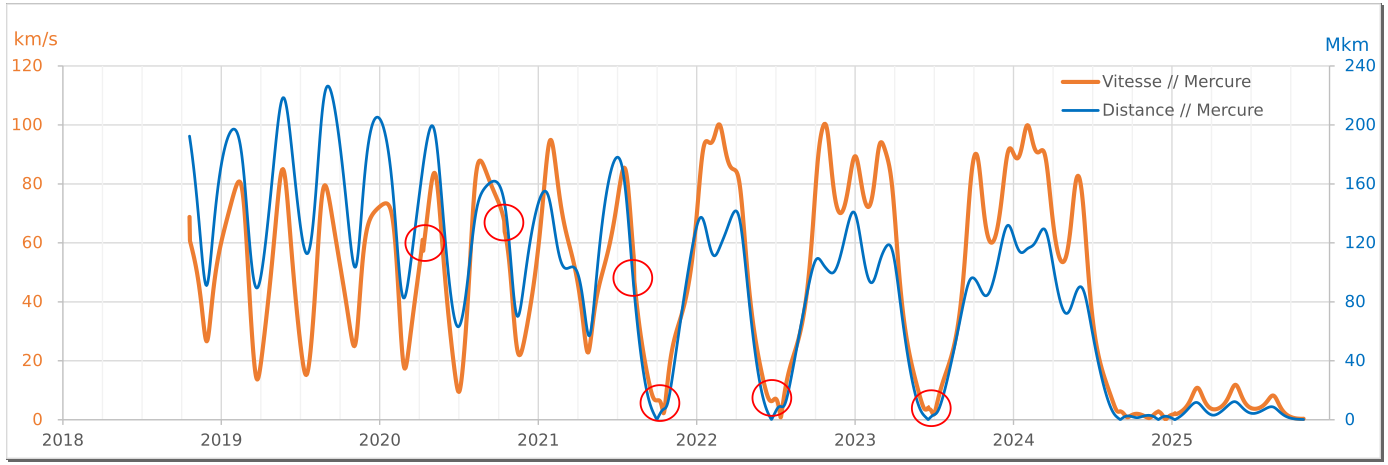
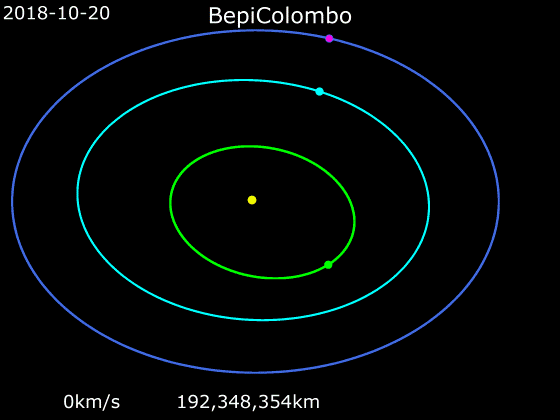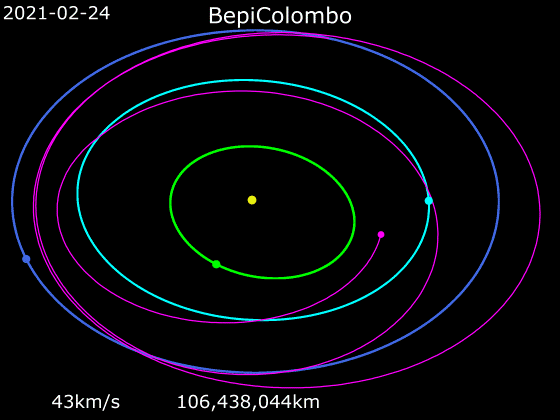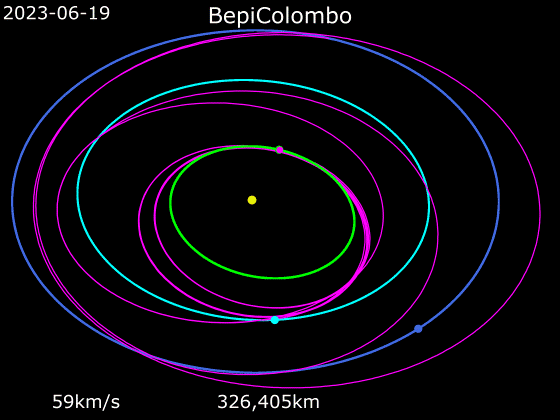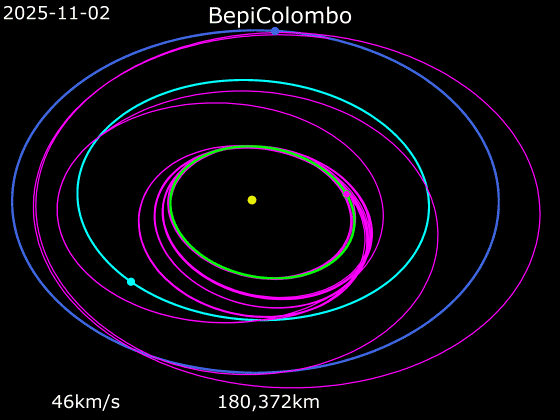
Un excellent exemple en cours est celui de la sonde lancée en octobre 2018 par l’ESA (agence spatiale européenne) et la JAXA (agence spatiale japonaise), BepiColombo, une grosse sonde de 4.100 kg. Cette sonde doit améliorer dans beaucoup de domaines notre connaissance de Mercure, la planète la plus petite et la plus proche du Soleil. Elle devrait se mettre en orbite fin 2025. Du fait de la proximité du Soleil la sonde spatiale est soumise à des températures oscillant entre −180 °C et +450 °C qui nécessitent le recours à différentes dispositifs (bouclier thermique) pour la protéger. Par ailleurs pour parvenir à se mettre en orbite autour de Mercure, BepiColombo doit énormément réduire sa vitesse : pour remplir cet objectif la sonde spatiale utilise une propulsion ionique, seule capable de produire une telle décélération sans imposer une trop grande masse d’ergols. Elle suit par ailleurs une trajectoire complexe d’une durée de 7,2 ans, durant laquelle elle survolera une fois la Terre, 2 fois Vénus et 6 fois Mercure, dont l’assistance gravitationnelle complète l’action de la propulsion. Notons que sur les six survols de Mercure par BepiColombo, les trois derniers ne sont pas réellement des assistances gravitationnelles mais bien plutôt des préparations à la mise en orbite mercurienne.

↑ Vitesse (km/s) et distance (millions km) par rapport à Mercure de BepiColombo entre le 20 octobre 2018 (lancement) et fin 2025 (insertion en orbite autour de la planète) durant son transit entre la Terre Mercure. Les cercles rouges correspondent aux survols de planète (avec assistance gravitationnelle).

–

4) Chondrites

C’est un terme utilisé en planétologie pour désigner un certain type de météorites pierreuses (moins de 35 % de métal). Cette catégorie renferme les météorites les plus primitives et est elle-même divisée en plusieurs sous-groupes de météorites : notamment les chondrites ordinaires, les chondrites carbonées et les chondrites à enstatite. La caractéristique des chondrites est de contenir des chondres. Ceux-ci sont des billes submillimétriques, majoritairement formées de silicates; le modèle standard de leur formation initiale est qu’ils sont engendrés lors de la condensation de la nébuleuse solaire, sous l’effet de décharges électriques au sein du nuage proto-solaire de poussière cosmique. Ces roches sont les plus anciennes du Système solaire d’une part en raison de l’âge auquel leurs différents éléments se sont rassemblés, d’autre part en raison du peu de transformation qu’ont subi ces éléments depuis qu’ils ont formé des minéraux. Les chondrites sont considérées comme les premiers éléments à partir desquels se sont formées les planètes. Les météorites pierreuses de type chondrite proviennent de la surface de petits astéroïdes qui ne se sont pas différenciés depuis leur formation il y a 4,56 milliards d’années, en même temps que le Système solaire. Les météorites provenant d’astéroïdes plus gros, voire de planètes comme Mars ou la Lune sont des roches dites fortement différenciées, c’est-à-dire dont la composition chimique et/ou minéralogique a été complètement modifiée par rapport au matériau primitif que représentent les chondrites; elles sont classées comme achondrites. Les météorites pierreuses sont assez proches des roches terrestres, en ce sens qu’elles contiennent en majorité des silicates, lesquels composent la plus grande partie des roches de notre planète. Certaines chondrites contiennent des minéraux hydratés (argiles), des inclusions minérales riches en calcium et en aluminium réfractaires (CAI pour Ca-Al-rich Inclusion, dont l’âge radio-chronmétriquement mesuré montre qu’ils sont parmi les premiers objets formés dans le système solaire dont nous avons la trace) et des grains pré-solaires. Le tout est noyé dans une matrice silicatée amorphe.

–

5) Distances et unités de distance en astronomie

En astronomie on utilise, selon les cas, différentes unités de distance :

a) Le kilomètre (km), on est vite dépassé par le nombre de zéros qu’on doit mettre derrière, mais c’est une unité qui parle à tout le monde. On s’en sert pour préciser le diamètre d’une planète ou d’un satellite, l’épaisseur d’une atmosphère ou encore la distance Terre-Lune.

b) L’unité astronomique (ua ou UA) qui est une unité qui sert essentiellement aux distances dans le système solaire ou dans les systèmes planétaires d’autres étoiles que la nôtre.

c) L’année-lumière (al ou AL), (unité de distance et pas de temps!) utile pour les très grandes distances galactiques, étoiles de la Voie Lactée, etc.

d) Le Parsec enfin, très utilisé par les astronomes professionnels et les astrophysiciens.

a) Le kilomètre : nul besoin d’explication, c’est 1.000 fois l’unité de distance internationale (le mètre), l’unité est connue de tous.

b) L’unité astronomique (ua) est très utile pour comparer les distances dans le système solaire. Il n’est pas très “parlant” à l’esprit de dire que Neptune est en moyenne à 4.503.443.661 kilomètres du Soleil…

On a donc inventé l’unité astronomique pour éviter ces chiffres à rallonges. Une unité astronomique c’est la distance moyenne entre la Terre et le Soleil, soit environ 150 millions de km (exactement 149 597 870 700 mètres ou 149 597 870,7 km). Retenez l’arrondi de 150 millions de km.

c) l’année-lumière (al), qui est bien une distance : c’est la distance que parcourt la lumière dans le vide en une année. La lumière se déplace à près de 300.000 kilomètres par seconde (299 792,458 km/s exactement). Il suffit de faire la multiplication pour arriver à : 365,25 j/an x 86 400 s/j x 299 792 458 m/s = 9 460 730 472 580 800 mètres par an, soit environ 9 460 milliards de kilomètres ! Difficilement concret au niveau de notre cerveau. Pourtant cette mesure est bien utile dans les galaxies et les espaces inter-galactiques. Il suffit de savoir que notre galaxie (la Voie Lactée) a un diamètre d’environ 100 000 al et une épaisseur de 15 000 al pour se rendre compte de l’impossibilité de mettre un chiffre en kilomètres ou même en ua pour mesurer une galaxie. C’est également parlant pour les étoiles : savoir que Véga (de la Lyre) est à 25 al, alors que sa voisine Deneb (du Cygne) est à 1 550 al nous montre que le ciel est en 3D, même si nous ne le voyons optiquement qu’en 2D.

d) le parsec, (symbole pc) est une unité de longueur utilisée en astronomie. Son nom vient de la contraction de « parallaxe-seconde ».

Le parsec était défini historiquement comme étant la distance à laquelle une unité astronomique (ua) sous-tend un angle d’une seconde d’arc. Un parsec vaut 3,085 678×10¹⁶ m, soit environ 206 265 unités astronomiques ((1/tan(1″)) ua exactement) ou 3,2616 années-lumière. La nouvelle définition officielle de 2012 de l’UAI (Union Astronomique Internationale) est légèrement différente, mais on arrive au même chiffre. Pour des raisons pratiques, les astronomes expriment souvent les distances des objets astronomiques en parsecs plutôt qu’en années-lumière. Cette unité permet une conversion directe des valeurs observées en distance : si la parallaxe annuelle d’une étoile est mesurée en secondes d’arc, alors la distance entre cette étoile et le Soleil, exprimée en parsecs, est égale à l’inverse de cette valeur. La magnitude absolue et le module de distance sont deux unités dérivées du parsec, et l’expression des distances en parsecs facilite la manipulation de ces données.

Cette unité résulte de l’utilisation d’une méthode trigonométrique dite « méthode de la parallaxe », servant à déterminer la distance séparant un observateur d’un objet éloigné quelconque, à la mesure de la distance des objets célestes

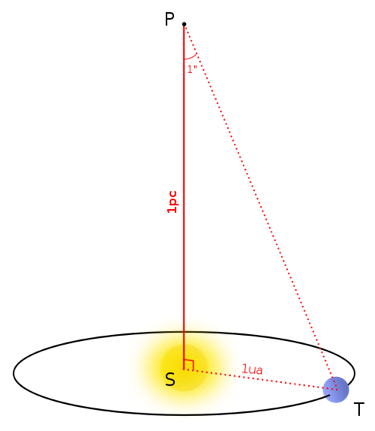Sur la figure, (d’échelle très réduite et ne respectant pas les valeurs angulaires), S est le Soleil, T la Terre et P un objet situé à un parsec du Soleil : par définition, l’angle du haut est égal à une seconde d’arc (1″) et la distance TS vaut une unité astronomique (1 UA). Grâce aux règles de trigonométrie, il est possible de calculer SP :

SP = TS/tan 1’’ soit environ 206 264,80624548 UA
Comme 1 UA = 1,49597870700 x 10¹¹ m
on a 1 pc = 206 264,80624548 x 1,49597870700 x 10¹¹ m
et donc 1 pc = 3,0856775814672 x 10¹⁶ m
donc 1 pc = 3,2616 années-lumière

Le choix d’une définition arbitraire mais désormais fixe de l’unité astronomique explique la précision des valeurs précédentes, qui pourrait surprendre a priori, et est toute théorique; les mesures astronomiques, en particulier celles des parallaxes, étant en pratique bien rarement meilleures qu’à 1 % près.

L’étoile la plus proche du Soleil, α Cen C (Proxima Centauri), se trouve à 1,316 parsec (4,28 années-lumière). Les distances des autres objets célestes n’appartenant pas au système solaire sont bien plus grandes et se mesurent couramment en kiloparsecs (symbole kpc) ou mégaparsecs (symbole Mpc). Les parallaxes ont des valeurs faibles : 0,76″ pour Proxima Centauri; aussi, la méthode parallactique ne permet guère de déterminer des distances stellaires supérieures à 100 parsecs environ, ce qui correspond à des mesures de parallaxe inférieures à 10 millisecondes d’arc. Entre 1989 et 1993, le satellite Hipparcos, lancé par l’Agence spatiale européenne, a mesuré la parallaxe d’environ 100 000 étoiles avec une précision supérieure à la milliseconde d’arc, ce qui a permis de déterminer la distance d’étoiles éloignées de nous de plus d’un kiloparsec.

En résumé :

1 parsec = (648 000/π) unités astronomiques ≈ 206 264,806 247 unités astronomiques;
1 parsec = (96 939 420 213 600 000/π) mètres ≈ 3,085 677 581 × 10¹⁶ mètres;
1 parsec = (96 939 420 213 600 000/(9 460 730 472 580 800×π)) années-lumière (= (10 246 429 500/(999 992 651×π)) années-lumière) ≈ 3,2616 années-lumière.

Historique des estimations de la distance moyenne de la Terre au Soleil (D) en rayons équatoriaux de la Terre (D/R) à partir de la parallaxe horizontale équatoriale du Soleil
	Parallaxe	D/R
Archimède, L’Arénaire (III^e siècle av. J.-C.)	40″	10 000
Aristarque de Samos, Des grandeurs et des distances (III^e siècle av. J.-C.)		380-1520
Hipparque (II^e siècle av. J.-C.)	7′	490
Posidonios (I^er siècle av. J.-C.), d’après Cléomède (I^er siècle)		10 000
Ptolémée (II^e siècle)	2′ 50″	1 210
Godefroy Wendelin (1635)	15″	14 000
Jeremiah Horrocks (1639)	15″	14 000
Christian Huygens (1659)	8.6″	24 000
Jean-Dominique Cassini et Jean Richer (1672)	9/1″	21 700
Jérôme de Lalande (1771)	8.6″	24 000
Simon Newcomb (1895)	8.80″	23 440
Arthur R. Hinks (1909)	8.807″	23 420
H. Spencer Jones (1941)	8.790″	23 466
aujourd’hui	8.794143″	23 455

Première mesure du rayon de la terre : elle a été conçue au III^e siècle av. J.-C. par Ératosthène.

Son calcul est simple : le Soleil est si éloigné que ses rayons arrivent parallèlement en tout point de la Terre.

Ératosthène a lu qu’à Syène (maintenant Assouan), les rayons tombent verticalement dans un puits à midi (solaire), le jour du solstice d’été. Cela veut dire que le Soleil passe par le zénith, il n’y a alors pas d’ombre. Plus au nord, au même moment, les rayons atteignent Alexandrie sous un angle non nul, qu’il mesure. L’angle mesuré est de 1/50^e de cercle. Cela signifie que la circonférence de la Terre est cinquante fois plus grande que la distance Syène-Alexandrie. Ératosthène avait lu également que les caravanes de dromadaires partant de Syène mettaient cinquante jours pour arriver à Alexandrie en parcourant cent stades par jour. Il calcula que la distance entre les deux villes de la vallée du Nil était de 5 000 stades. Le stade équivaut à 158 m. Par la mesure de l’ombre portée par ces objets de hauteur connue situés en deux points de latitude différente, il trouve la valeur de 250 000 stades (soit 39 500 km) pour la longueur du méridien, c’est-à-dire la circonférence terrestre. Cette mesure est exacte à 2 % près ! Il en déduisit le rayon de la Terre. Notons aussi l’extraordinaire précision de l’estimation faite par Huygens en 1659, qui n’est qu’à 2,3 % de la taille réelle mesurée aujourd’hui.

Distance moyenne des planètes du Système solaire au Soleil

Mercure: 0,38 ua (57 Mkm [millions de km])
Vénus: 0,72 ua (108 Mkm)
Terre: 1,00 ua (150 Mkm)
Mars: 1,52 ua (228 Mkm)
Jupiter: 5,21 ua (781 Mkm)
Saturne: 9,54 ua (1 431 Mkm)
Uranus: 19,18 ua (2 877 Mkm)
Neptune: 30,11 ua (4 516 Mkm)

Autres distances au Soleil

Ceinture d’astéroïdes: entre 2 et 3,5 à 4 ua (300 à 600 Mkm)
Pluton: de 29 à 49 ua (4 350 à 7 350 Mkm)
Ceinture de Kuiper: de 30 à 55 ua (4 500 à 8 250 Mkm)
Sonde Voyager 1 (lancée le 5 septembre 1977) : à 139 ua du Soleil (août 2017) soit plus de 20,9 milliards de km). Vitesse : ~ 23.600 km/h
Sonde Voyager 2 (lancée le 20 août 1977) : à 115,1 ua du Soleil (août 2017) soit plus de 17,3 milliards de km. Vitesse : ~ 21.373 km/h
Nuage d’Oort: environ de 20 000 à 30 000 ua jusqu’à 155 000 ua (de 3 000 à 23 250 milliards de km)

Il est plus facile de dire et de comprendre que Neptune est à environ 30 UA, soit trente fois plus loin du soleil que nous, que de manipuler le chiffre de 4 516 000 000 km pour dire la même chose !

–

6) L’Écliptique

D’un point de vue géocentrique (vu de la Terre), l’écliptique est le grand cercle représentant la projection, sur la sphère céleste, de la trajectoire annuelle apparente du Soleil vue de la Terre. D’un point de vue héliocentrique (vu du Soleil), il s’agit de l’intersection de la sphère céleste avec le plan écliptique (plan géométrique contenant l’orbite de la Terre autour du Soleil).

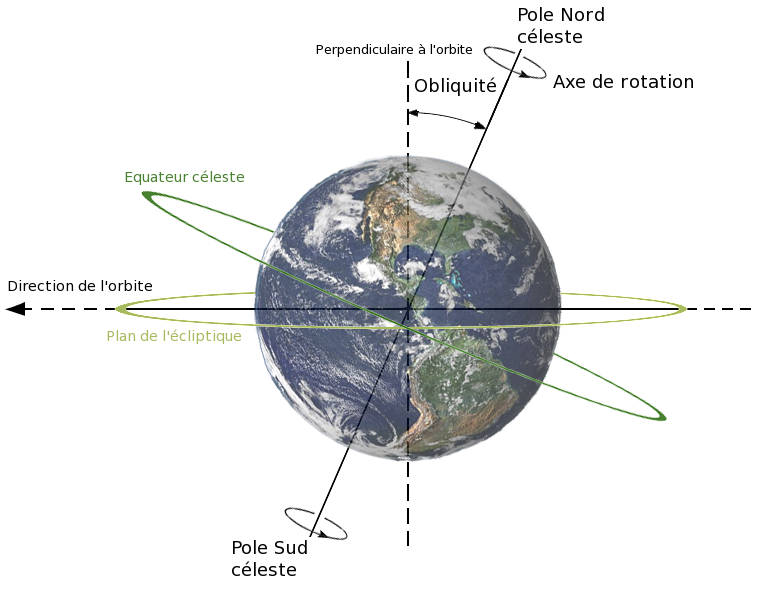Le plan de l’écliptique est le plan de référence du système de coordonnées célestes dit système de coordonnées écliptiques.

Donc la Terre décrit son orbite autour du Soleil et définit ainsi un plan. C’est ce plan qu’on appelle l’écliptique. Il se trouve que les autres planètes du système solaire tournent à peu près dans le même plan et sont également proches de la ligne de l’écliptique dans notre ciel. Donc, de notre point de vue “terrien”, les planètes (et la Lune) se déplacent dans le ciel le long de la même ligne courbe.

La Terre étant inclinée, son axe de rotation sur elle-même fait un angle d’environ 23° par rapport à l’écliptique. C’est ce qui fait que nous avons des saisons. Suivant les saisons, depuis la Terre, la ligne de l’écliptique est plus ou moins haute dans le ciel. Tout le monde a remarqué qu’en été à midi, le Soleil est plus haut dans le ciel qu’à la même heure en hiver !

–

7) Kelvin

C’est une mesure de température : Notez bien que la plupart des températures mentionnées dans les documents d’astronomie sont exprimées en Kelvins, échelle la plus utilisée par les scientifiques.

Zéro Kelvin (le zéro absolu) est équivalent à – 273,15 ° C.

Les Kelvins sont les mêmes degrés que les degrés centigrades (ou Celsius), seul le référentiel, la base (le point zéro) change. Quand une augmentation ou une diminution de 10 kelvins intervient, la conversion en degrés celsius augmentera ou diminuera aussi de 10 degrés dans cette échelle.

Il faut donc retrancher 273,15 aux températures en K pour les obtenir en °C. Ex : 84 K = 84 – 273 = -189°C.

On ne dit pas « un degré Kelvin », mais simplement « un kelvin ».

–

8) Kepler (Lois de Kepler)

Première loi – Loi des orbites

Les planètes du système solaire décrivent des trajectoires elliptiques, dont le Soleil occupe l’un des foyers.

Dans le référentiel héliocentrique, le Soleil occupe toujours l’un des deux foyers de la trajectoire elliptique des planètes qui gravitent autour de lui. À strictement parler, c’est le centre de masse qui occupe ce foyer; la plus grande différence est atteinte avec Jupiter qui, du fait de sa masse importante, décale ce centre de masse de 743 075 km; soit 1,07 rayons solaires — des déplacements plus importants peuvent être obtenus en cumulant les effets des planètes sur leur orbite.

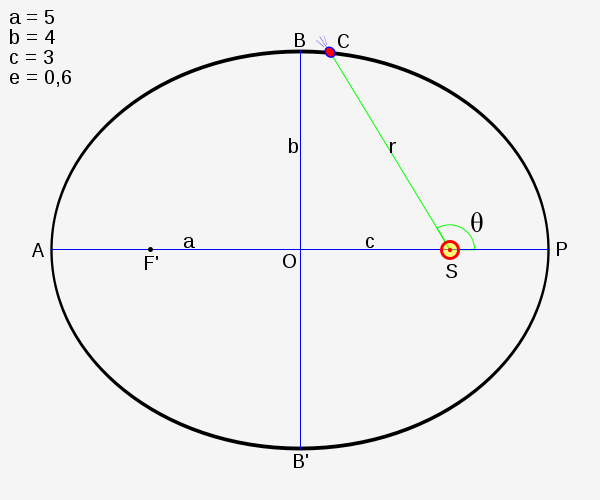
Schéma d’une orbite elliptique, l’excentricité étant très exagérée vis-à-vis de celles des planètes du système solaire

Les ellipses que décrivent les centres de gravité des planètes sont quasi-circulaires, ayant une faible ou très faible excentricité orbitale, les plus élevées étant celles de Mercure (~0,2), suivie de celle de Mars (~0,09). C’est cette dernière que Kepler a utilisée pour sa découverte de la première loi, et il est aidé en cela par la faiblesse de l’excentricité de l’orbite de la Terre (~0,017) relativement à celle de Mars. Les foyers sont eux bien distincts du centre de l’ellipse.

Deuxième loi – Loi des aires

Si S est le Soleil et M une position quelconque d’une planète, l’aire balayée par le segment [SM] entre deux positions C et D est égale à l’aire balayée par ce segment entre deux positions E et F si la durée qui sépare les positions C et D est égale à la durée qui sépare les positions E et F. La vitesse d’une planète devient donc plus grande lorsque la planète se rapproche du Soleil. Elle est maximale au voisinage du rayon le plus court (périhélie), et minimale au voisinage du rayon le plus grand (aphélie).

De cette deuxième loi, on déduit que la force exercée sur la planète est constamment dirigée vers le Soleil. Kepler écrira à un collègue : Une chose est certaine : du Soleil émane une force qui saisit la planète.

De la loi des aires découle directement l’équation de Kepler qui permet de trouver l’aire parcourue en fonction de la position exacte d’une planète.

En effet la deuxième loi de Kepler implique que la planète accélère en approchant du Soleil et décélère en s’éloignant du Soleil. La vitesse n’est donc pas constante mais seulement l’aire parcourue. C’est pourquoi à ${\frac {T}{4}}$ la planète n’a pas parcouru un angle de 90° mais a balayé une aire de ${\frac {\text{Aire Totale}}{4}}$ .

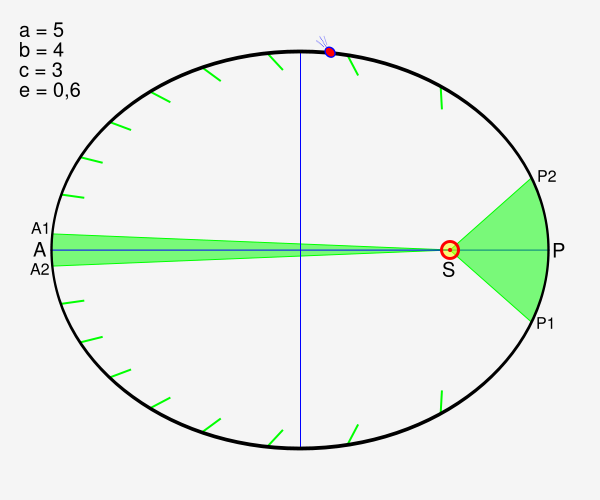
Loi des aires : chaque intervalle correspond à 5 % de la période

L’équation est de la forme $M = E - e sin ( E ).$ Avec M l’aire parcourue (connue sous le nom d’anomalie moyenne), e l’excentricité et E l’angle au centre de l’ellipse.

La réciproque de l’équation de Kepler qui revient à trouver l’angle de la planète en fonction de l’aire (et donc du temps), ne possède pas de résolution exacte. Mais il existe des formes approchées sous forme de sommes infinies ainsi que des approximations grâce à la méthode de Newton.

Troisième loi – Loi des périodes

Le carré de la période sidérale P d’une planète (temps entre deux passages successifs devant une étoile lointaine) est directement proportionnel au cube du demi-grand axe a de la trajectoire elliptique de la planète :

$\left(\frac{2\pi}{P}\right)^2\cdot a^3=k$

avec k constant. Les lois de la gravitation universelle énoncées par Isaac Newton permettent de déterminer cette constante en fonction de la constante gravitationnelle G, de la masse du Soleil M_⊙ et de la masse de la planète m gravitant autour du Soleil selon

$k = G (M_\odot+m)$

soit, avec M>>m

k = G M_\odot

En exprimant les distances en unités astronomiques et les périodes en années, la loi s’exprime très simplement :

P=k'{\sqrt {a^{3}}}

De cette troisième loi, appelée aussi « loi harmonique de Kepler » (car elle exprime un invariant à travers tout le système solaire, « donc » une certaine harmonie de celui-ci, le mouvement de toutes les planètes étant unifié en une loi universelle), on déduit qu’il existe un facteur constant entre la force exercée et la masse de la planète considérée, qui est la constante de gravitation universelle, ou constante gravitationnelle.

Cette formule, avec celles de l’ellipse, permet de calculer les différents paramètres d’une trajectoire elliptique à partir de très peu d’informations. En effet, Johann Lambert (1728 – 1777) montra que la connaissance de trois positions datées permettaient de retrouver les paramètres du mouvement.

–

9) Géocentrisme et Héliocentrisme

Ce sujet était trop vaste pour continuer à figurer dans ce glossaire. C’est pourquoi nous l’avons supprimé du glossaire et remplacé par un document pdf accessible dans le sous-menu “Téléchargements / Nos documents pdf”.

La différence entre ces deux systèmes de manière très synthétique :

Le Géocentrisme pose comme principe que la Terre est au centre de l’Univers et que le Soleil et les planètes tournent autour de la Terre. Cette vision des choses, plus philosophique que scientifique a perduré depuis l’époque d’Aristote (III° siècle avant J.C) et de Claude Ptolémée (1^er siècle après J.C) jusqu’au milieu du XVII° siècle. L’Église catholique romaine en avait fait un dogme intangible.

L’Héliocentrisme place le Soleil au centre, avec les planètes (dont la Terre) qui tournent autour de lui. D’abord évoquée par l’astronome grec Aristarque de Samos au III° siècle avant J.C. puis oubliée, cette vision du monde a été développée bien plus tard par le moine polonais Nicolas Copernic au XVI° siècle puis par Galilée au XVII° siècle.

Vous pouvez également accéder à ce document directement en cliquant ici !

–

10) Newton (Lois de Newton)

Isaac Newton (1643 – 1727), un philosophe, mathématicien, physicien, alchimiste, astronome et théologien anglais est l’un des plus grands génies de l’histoire de l’astronomie, voire même de l’histoire tout court !

Il a énoncé, dans son ouvrage “Philosophiæ naturalis Principia Mathematica” plusieurs lois qui vont s’avérer essentielles dans la mécanique céleste :
1) Les 3 lois du mouvement
2) La loi sur la gravitation universelle

Première édition des «Principia Mathematica» annotée de la main d’Isaac Newton

1 – Les 3 lois du mouvement :

Première loi : Principe d’inertie

« Tout corps persévère dans l’état de repos ou de mouvement uniforme en ligne droite dans lequel il se trouve, à moins que quelque force n’agisse sur lui, et ne le contraigne à changer d’état. »

Dans la formulation moderne de la loi, on parle de mouvement rectiligne uniforme, et on remplace la notion de force (unique) par celle, plus générale, de résultante des forces appliquées sur le corps. Autrement dit, s’il n’y a pas de force qui s’exerce sur un corps (corps isolé), ou si la somme des forces (ou force résultante) s’exerçant sur lui est égale au vecteur nul (corps pseudo-isolé), la direction et la norme de sa vitesse est constante ou, ce qui revient au même, son accélération est nulle. Cette première loi infirme la conception héritée d’Aristote, selon laquelle pour maintenir la vitesse d’un mobile constante, il était nécessaire de lui appliquer une force continue (justement pour “annuler” les forces dues aux frottements qui ne sont pas nulles en dehors du vide et de toute influence gravitationnelle). Le mouvement considéré par Newton a lieu par rapport à un espace mathématique abstrait qu’il suppose absolu. Sa première loi s’applique également dans des référentiels en translation uniforme par rapport à cet espace absolu, ce qui donne naissance à la notion de référentiel galiléen. A^u XIX° siècle, la notion d’espace absolu est peu à peu abandonnée au profit des seuls référentiels galiléens. La première loi de Newton se reformule donc aujourd’hui sous la forme :

Dans un référentiel galiléen, le vecteur vitesse du centre d’inertie d’un système est constant si et seulement si la somme des vecteurs forces qui s’exercent sur le système est un vecteur nul.

Problème du référentiel galiléen : Un référentiel galiléen est un référentiel dans lequel la première loi de Newton est vérifiée. Ainsi la première loi de Newton ne s’applique que dans un référentiel galiléen et un référentiel galiléen est un référentiel où la première loi de Newton s’applique…!! ce qui semble être une définition circulaire. Pour éviter ce problème, on réécrit le principe d’inertie sous la forme axiomatique suivante :

Il existe une famille de référentiels, appelés galiléens ou inertiels, tels que, par rapport à l’un de ces référentiels, tout point matériel pseudo-isolé (qui est soumis à des forces externes dont la somme est nulle) est soit au repos, soit animé d’un mouvement rectiligne uniforme.

La détermination d’un bon référentiel galiléen est en réalité expérimentale et comme souvent en physique, seule la cohérence entre la théorie (ici la première loi de Newton) et la mesure (mouvement rectiligne uniforme) valide le choix a posteriori.

Deuxième loi : principe fondamental de la dynamique de translation

« Les changements qui arrivent dans le mouvement sont proportionnels à la force motrice; et se font dans la ligne droite dans laquelle cette force a été imprimée. »

Dans sa version moderne, on la nomme principe fondamental de la dynamique (PFD), parfois appelée relation fondamentale de la dynamique (RFD), et s’énonce ainsi : Dans un référentiel galiléen, la dérivée de la quantité de mouvement est égale à la somme des forces extérieures qui s’exercent sur le solide :Cette expression se simplifie dans le cas où la masse est constante : Soit un corps de masse m (constante) : l’accélération subie par ce corps dans un référentiel galiléen est proportionnelle à la résultante des forces qu’il subit, et inversement proportionnelle à sa masse m.

Ceci est souvent récapitulé dans l’équation :

où

Troisième loi : principe des actions réciproques

« L’action est toujours égale à la réaction ; c’est-à-dire que les actions de deux corps l’un sur l’autre sont toujours égales et de sens contraires. » — Newton

De manière moderne, on exprime que :

Tout corps A exerçant une force sur un corps B subit une force d’intensité égale, de même direction mais de sens opposé, exercée par le corps B.

A et B étant deux corps en interaction, la force (exercée par A sur B) et la force (exercée par B sur A) qui décrivent l’interaction sont directement opposées :

Ces forces ont la même droite d’action, des sens opposés et la même norme. Ces deux forces sont toujours directement opposées, que A et B soient immobiles ou en mouvement.

Il faut là encore revenir sur la modélisation, c’est-à-dire sur le passage de la réalité à la description vectorielle. Dans le cas d’une action de contact, c’est assez simple : si Albert pousse de 100 N sur Béatrice, alors Béatrice pousse également de 100 N sur Albert; Albert et Béatrice peuvent être sur un sol adhérent ou de la glace, immobiles ou en train de patiner. Il est souvent plus difficile de comprendre que si Albert s’appuie sur le mur, alors le mur pousse aussi sur Albert; le mur n’a pas de « volonté motrice », il fléchit sous l’effet de l’action d’Albert mais cette flexion est indécelable sauf pour une paroi souple, et Albert subit donc un « effet ressort ». Il est de même pour la notion de sol qui soutient Albert; en particulier, en cas de saut, il est difficile d’imaginer que c’est le sol qui propulse Albert, toujours par effet ressort.

Le cas des actions à distance est également difficile à conceptualiser, en particulier le fait qu’Albert attire lui aussi la Terre…

Cette loi est parfois appelée loi d’action-réaction, en référence à l’énoncé original; une formulation au mieux imprécise, au pire entraînant de nombreuses confusions. En particulier, cette ancienne formulation véhicule l’idée qu’il y a toujours une force qui est la « cause » (l’action), l’autre n’étant qu’une sorte de conséquence (la réaction).

La loi des actions réciproques a l’inconvénient de supposer l’application des forces comme instantanée (ce qui est abandonné en relativité restreinte). Dans le cas des forces à distance, il convient dans certains cas d’effectuer des transformations pour tenir compte du retard de propagation. Cette correction ne relève pas de la relativité. Comme les forces électromagnétiques s’appliquent à distance, on avait mis en évidence que ces forces se propagent à la vitesse de la lumière et non à vitesse infinie et inclus cette nuance dans les équations avant la révolution de la relativité restreinte.

2 – La loi de la gravitation universelle

La loi de la gravitation ou loi de l’attraction universelle, découverte par Isaac Newton, est la loi décrivant la gravitation comme une force responsable de la chute des corps et du mouvement des corps célestes, et de façon générale, de l’attraction entre des corps ayant une masse, par exemple les planètes, les satellites naturels ou artificiels. On voit ici essentiellement les aspects de la mécanique classique de la gravitation, et non pas celle de la relativité générale d’Einstein qui procède d’un cadre plus général dans un nouveau paradigme.

Deux corps ponctuels de masses respectives $M A et$ $M B$ s’attirent avec des forces de mêmes valeurs (mais vectoriellement opposées), proportionnelles aux produits des deux masses, et inversement proportionnelle au carré de la distance qui les sépare. Cette force a pour direction la droite passant par les centres de gravité de ces deux corps.

La force exercée sur le corps $B$ par le corps $A$ est donnée par :

${F}_{{A/B}}={F}_{{B/A}}=G{\frac {M_{A}M_{B}}{d^{2}}}$

$M A$ et $M B$ en kilogrammes (kg), d en mètres (m); F_A/B et $F B/A$ en newtons (N).

où G est la constante gravitationnelle, elle vaut dans les unités SI (Système International d’unités) :

G = 6,67191 × 10⁻¹¹ N⋅m²⋅kg⁻² ou

G = 6,67191 × 10⁻¹¹ m³⋅kg⁻¹. s^-2

G correspond à la force entre deux masses d’un kilogramme chacune, distantes d’un mètre.

–

11) Lagrange

Joseph Louis, comte de Lagrange (en italien Giuseppe Ludovico De la Grange Tournier), né à Turin en 1736 et mort à Paris en 1813, est un mathématicien, mécanicien et astronome italien naturalisé français. À l’âge de trente ans, il quitte le Piémont et va séjourner à Berlin pendant vingt-et-un ans. Ensuite, il s’installe pour les vingt-six dernières années de sa vie à Paris, où il obtient la nationalité française sur l’instance d’Antoine Lavoisier.

Les points de Lagrange

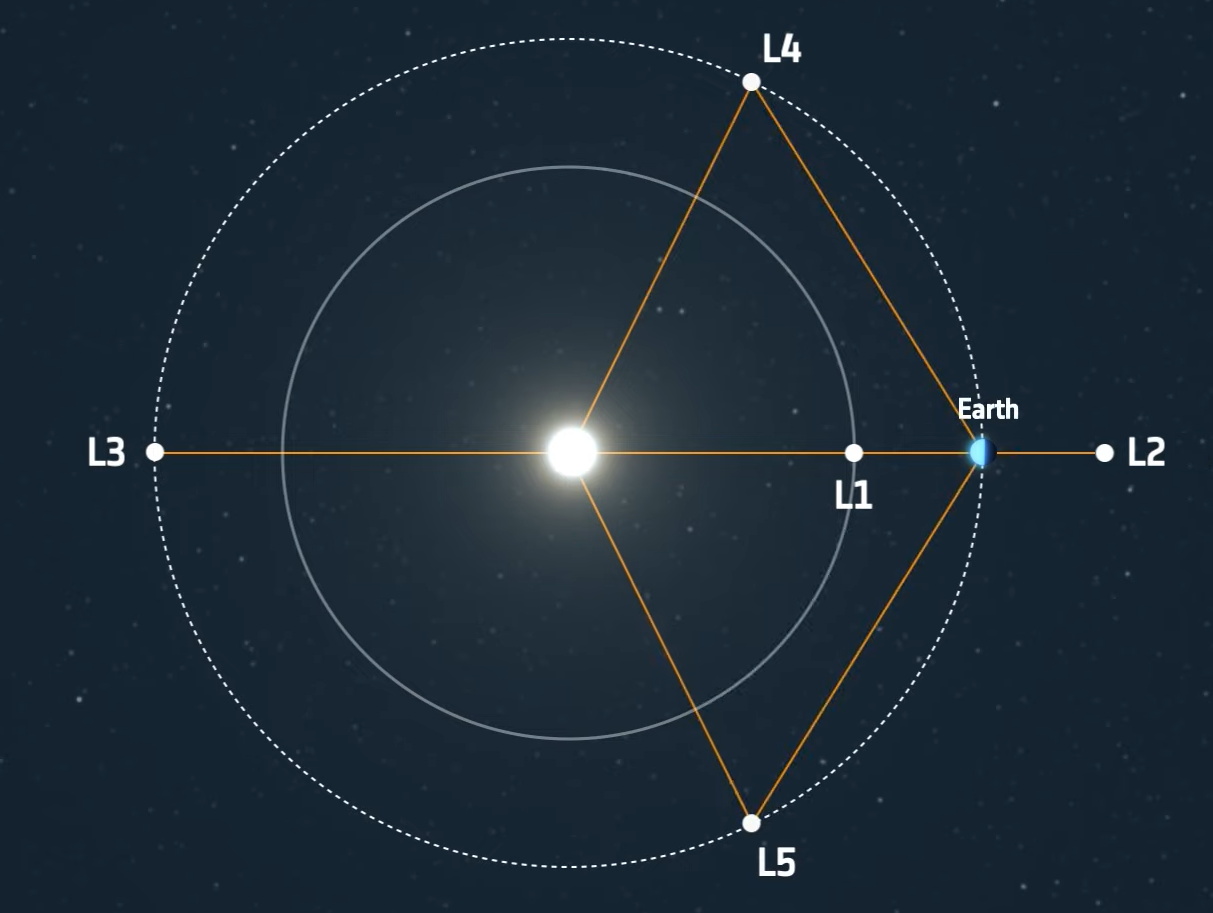
Un point de Lagrange (noté L₁ à L₅), ou, plus rarement, point de libration, est une position de l’espace où les champs de gravité de deux corps en orbite l’un autour de l’autre, et de masses substantielles, fournissent exactement la force centripète requise pour que ce point de l’espace accompagne simultanément l’orbite des deux corps. Dans le cas où les deux corps sont en orbite circulaire, ces points représentent les endroits où un troisième corps de masse négligeable resterait immobile par rapport aux deux autres, au sens où il accompagnerait à la même vitesse angulaire leur rotation autour de leur centre de gravité commun sans que sa position par rapport à eux n’évolue. Au nombre de cinq, ces points se scindent en deux points stables dénommés L₄ et L₅, et en trois points instables notés L₁ à L₃. Ils sont nommés en l’honneur du mathématicien français Joseph-Louis Lagrange. Ils interviennent dans l’étude de certaines configurations d’objets du Système solaire (principalement pour les points stables) et dans le placement de divers satellites artificiels (principalement pour les points instables). Ce sont les points remarquables de la « géométrie de Roche » (points-col et extrema) laquelle permet notamment de classer les différents types d’étoiles binaires. Les trois points L₁, L₂ et L₃ sont parfois appelés les points d’Euler, en l’honneur de Leonhard Euler, l’appellation de points de Lagrange étant alors réservées aux deux points L₄ et L₅.

En mécanique céleste, il est un sujet qui a passionné de nombreux mathématiciens : c’est le problème dit des trois corps. Newton, après avoir énoncé sa loi qui exprime que « les corps s’attirent avec une force proportionnelle au produit de leur masse et inversement proportionnelle au carré de la distance de leurs centres », a cherché à décrire le comportement de trois corps sans y parvenir. Il faut attendre le mathématicien Joseph-Louis Lagrange qui, en 1772, étudia le cas d’un petit corps, de masse négligeable (ce qu’on appelle aujourd’hui corps d’épreuve ou particule-test), soumis à l’attraction de deux plus gros : le Soleil et, par exemple, une planète. Il découvrit qu’il existait des positions d’équilibre pour le petit corps, des endroits où toutes les forces se compensent. Un objet de faible masse situé en ces points n’en bouge plus relativement aux deux autres corps, et tourne de concert avec eux (par exemple une planète et le Soleil).

Trois des points de Lagrange sont situés sur l’axe reliant les deux corps. Dans le cas d’une grande dissymétrie de masse entre ceux-ci, deux points sont situés proches et de part et d’autre du corps peu massif, alors que le troisième est quasiment situé à l’opposé du corps peu massif par rapport au corps massif.

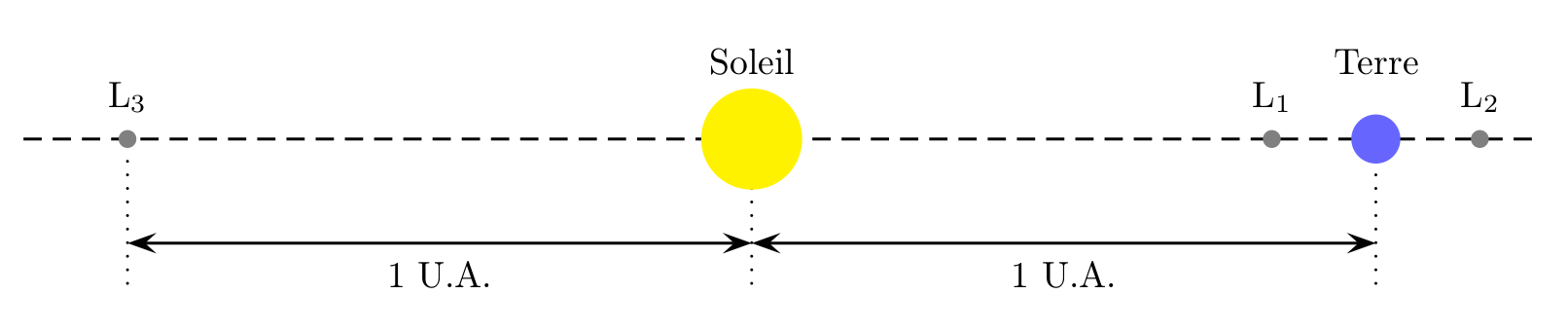
Si on donne en exemple les points de Lagrange du système Soleil-Terre, ces cinq points sont notés et définis comme suit (échelle non respectée) :

L₁: sur la ligne définie par les deux masses, entre celles-ci, la position exacte dépendant du rapport de masse entre les deux corps; dans le cas où l’un des deux corps a une masse beaucoup plus faible que l’autre, le point L₁ est situé nettement plus près du corps peu massif que du corps massif.
L₂: sur la ligne définie par les deux masses, au-delà de la plus petite. Dans le cas où l’un des deux corps a une masse beaucoup plus faible, la distance de L₂ à ce corps est comparable à celle entre L₁ et ce corps.
L₃: sur la ligne définie par les deux masses, au-delà de la plus grande. Dans le cas où l’un des deux corps est notablement moins massif que l’autre, la distance entre L₃ et le corps massif est comparable avec celle entre les deux corps.

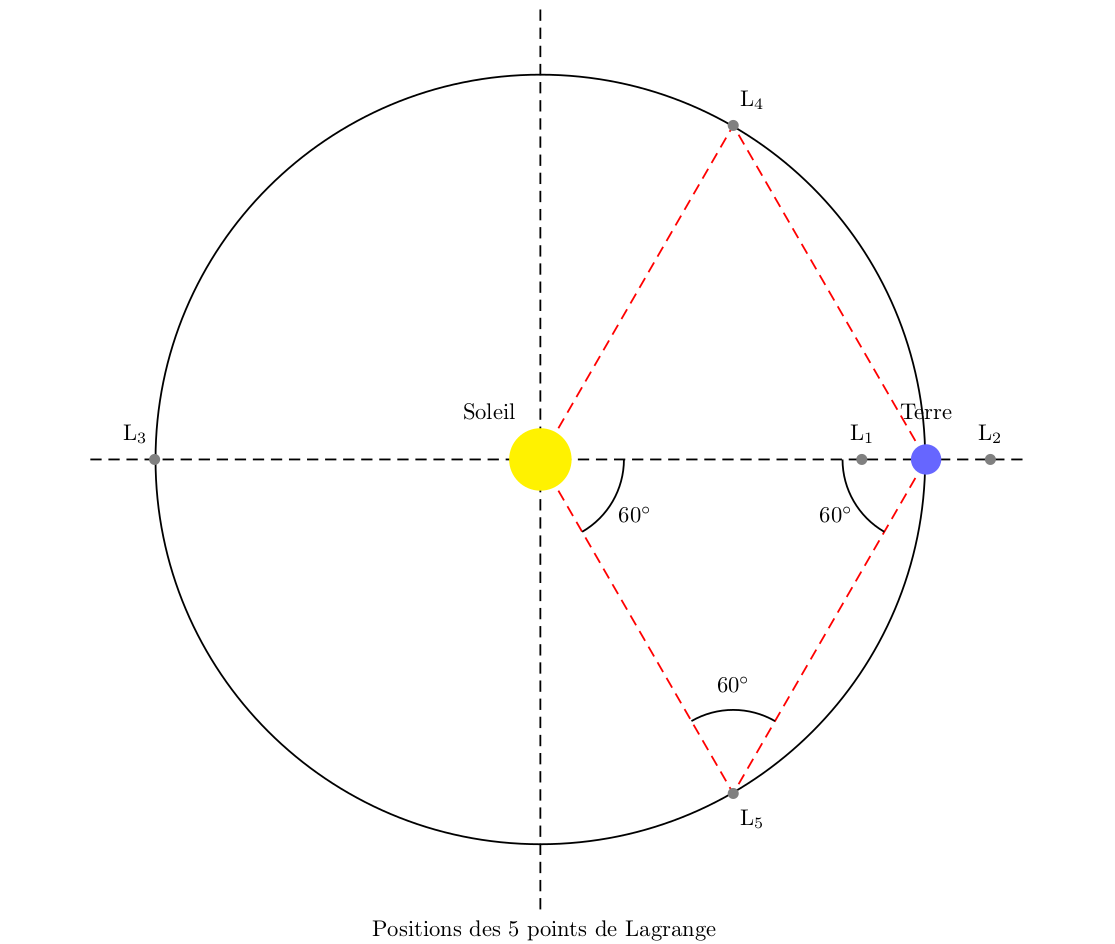
Les deux derniers points de Lagrange forment avec les deux corps des triangles équilatéraux

L₄ et L₅: sur les sommets des deux triangles équilatéraux dont la base est formée par les deux masses. Sans qu’il y ait de consensus précis, L₄ est celui des deux points en avance sur l’orbite de la plus petite des masses, dans son orbite autour de la grande, et L₅ est en retard. Ces points sont parfois appelés points de Lagrange triangulaires ou points Troyens, du fait que c’est le lieu où se trouvent les astéroïdes troyens du système Soleil-Jupiter. Contrairement aux trois premiers points, ces deux derniers ne dépendent pas des masses relatives des deux autres corps.

Les points L₁ et L₂ sont des équilibres instables, ce qui les rend utilisables dans le cadre de missions spatiales : on n’y trouve pas de corps naturels, et un équilibre dynamique peut y être maintenu pour une consommation de carburant raisonnable (le champ gravitationnel étant faible dans leur voisinage). Pour de tels satellites, des corrections de trajectoires régulières doivent être appliquées afin de conserver le satellite au voisinage du point. Ce temps caractéristique peut être évalué dans le cas où le rapport de masse des deux corps du système est élevé.

Les principaux avantages de ces positions, en comparaison des orbites terrestres, sont leur éloignement de la Terre et leur exposition au Soleil constante dans le temps. Le point L₁ se prête particulièrement à l’observation du Soleil et du vent solaire. Ce point a été occupé pour la première fois en 1978 par le satellite ISEE-3, et est actuellement occupé par les satellites SoHO et Advanced Composition Explorer. Le point L₂ est à l’inverse particulièrement intéressant pour les missions d’observation du cosmos, qui embarquent des instruments de grande sensibilité devant être détournés de la Terre et de la Lune, et fonctionnant à très basse température. Il est actuellement occupé par les satellites Herschel, Planck, WMAP et Gaia.

Il a été un temps envisagé de placer un télescope spatial au point L₄ ou L₅ du système Terre-Lune, mais cette option a été abandonnée après que des nuages de poussière y ont été observés.

Autre schéma des Points de Lagrange

Troyens, objets troyens (satellites, astéroïdes,…)

Les points L₄ et L₅ sont généralement stables, aussi on y trouve de nombreux corps naturels, dits troyens (satellites ou astéroïdes) :

dans le système Soleil-Jupiter, on recense (en 2011) environ 6.300 astéroïdes aux points L₄ et L₅
dans le système Soleil-Neptune, huit
dans le système Soleil-Mars, quatre
dans le système Saturne-Téthys, les points L₄ et L₅ sont occupés par Télesto et Calypso, respectivement
dans le système Saturne-Dioné, Hélène et Pollux occupent ces points

Curieusement, il semblerait que le système Soleil-Saturne ne soit pas en mesure d’accumuler des troyens du fait des perturbations joviennes.

Dans le système Soleil-Terre, on connait (depuis peu) un troyen au point L₄, l’astéroïde 2010 TK7, qui mesure 300 mètres de diamètre. Certains astronomes soulignent que cet objet pourrait représenter un risque comparable aux géocroiseurs. Ces auteurs proposent également que l’impacteur supposément à l’origine de la Lune (Théia) aurait stationné un temps sur le point L₄ ou L₅ et accumulé de la masse avant d’en être éjecté sous l’action des autres planètes.

–

12) La Libration

En astronomie, la libration (du latin libro -are, « mettre en équilibre, se balancer ») est une lente oscillation, réelle ou apparente, d’un satellite tel que vu à partir du corps céleste autour duquel il orbite. Utilisé seul, ce terme fait généralement référence aux mouvements apparents de la Lune relativement à la Terre, qui peuvent être comparés aux oscillations des deux plateaux d’une balance autour du point d’équilibre.

Un des premiers à décrire le phénomène de librations est Galilée, qui parla « [d’une] étrange particularité, nous voyons plus que la stricte moitié de la Lune ». De nombreux astronomes et mathématiciens ont entrepris ensuite d’expliquer et de modéliser les mouvements de la Lune. Parmi eux, Tobias Mayer, de Göttingen, a donné vers 1750 une explication géométrique des librations. À l’aube du XIX° siècle, les Français Joseph Louis Lagrange et Pierre Simon de Laplace ont développé les outils mathématiques qui ont permis de déterminer les tables de la Lune avec une grande précision.

La rotation de la Lune sur son axe est synchrone avec sa révolution autour de la Terre : elle tourne sur elle-même et effectue une révolution complète en 27,322 jours.

Si l’orbite de la Lune était parfaitement circulaire et si son axe de rotation était rigoureusement perpendiculaire au plan de son orbite, une personne située sur Terre observerait toujours les mêmes 50% de la surface lunaire si elle effectuait toujours ses observations à la même heure. Au lieu de cela, les phénomènes de libration lunaire lui permettent d’observer des parties légèrement différentes de sa surface à des moments différents. Des observations fines montrent qu’un total de 59 % de la surface de la Lune peut être observé depuis la Terre. En fait, nous avons 41 % qui restent visibles en permanence, 18 % qui sont successivement dévoilés par la libration au cours des lunaisons, et enfin 41 % qui ne sont jamais visibles depuis la Terre (et à un instant donné depuis un lieu donné on ne peut voir que 49,8 % de la surface lunaire).

Cette animation montre un ensemble de vues simulées de la Lune sur une période d’un mois, comme si une photographie avait été prise chaque jour à la même heure. Elle permet de mettre en évidence le phénomène de libration lunaire

Ces phénomènes peuvent prendre quatre formes différentes : les librations en longitude, les librations en latitude, les librations parallactiques et les librations physiques.

a) Les librations en longitude

Si la Lune tournait autour de la Terre en un cercle parfait (ellipse d’excentricité nulle), sa vitesse de translation serait uniforme (2° loi de Kepler) et donc toujours strictement opposée, en termes de vitesse angulaire observée depuis la Terre, à sa vitesse de rotation. Il n’y aurait donc pas de libration en longitude. Toutefois, les perturbations gravitationnelles dues aux autres corps du système solaire, ainsi qu’aux hétérogénéités de répartition de masse au sein des corps terrestre et lunaire entraînent des irrégularités dans le mouvement de révolution géocentrique lunaire, qui se traduit par une orbite dont l’excentricité varie autour d’une valeur moyenne de 0,0549.

La Lune parcourt donc son orbite avec une vitesse variable (2° loi de Kepler). Ainsi, quand elle s’éloigne de son périgée (quart de cercle de la flèche noire sur l’illustration), elle met moins de temps pour parcourir un quart de son orbite que pour pivoter de 90° sur son axe : la Lune laisse alors voir une mince bande supplémentaire de son bord Est (vu de la Terre). À l’inverse, lorsqu’elle s’éloigne de son apogée (à l’opposé de la flèche noire sur l’illustration), sa vitesse de translation, minimale, devient inférieure à sa vitesse de rotation, et la Lune laisse voir plus largement son bord Ouest (vu de la Terre). De façon imagée, la Lune semble dire « non » de la tête.

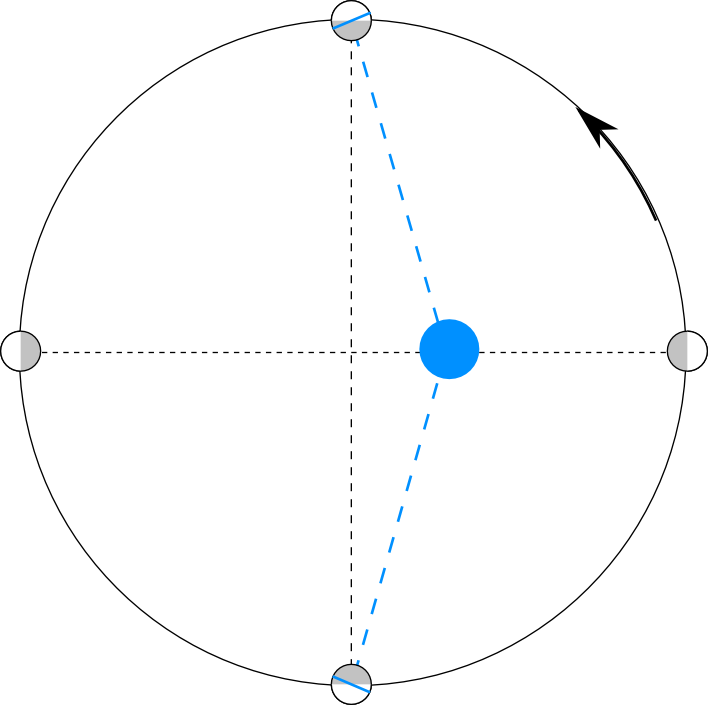
NB : Sur l’illustration, la moitié grisée de la Lune n’est pas bien placée. En effet, la moitié gauche de l’orbite est parcourue plus lentement, donc en davantage de temps, donc la moitié grisée pivote de davantage qu’un demi-tour. Et inversement dans la moitié droite de l’orbite : moins d’un demi-tour. Le texte est plus exact que l’illustration.

La valeur de la libration en longitude se situe autour de 7° 54′ (donc un total de deux fuseaux d’un peu moins de 8° chacun au cours d’une lunaison).

b) Les librations en latitude

La libration en latitude est due au fait que l’axe de rotation de la Lune n’est pas perpendiculaire au plan de son orbite : la Lune conserve cet angle de 6,7° tout au long de sa course orbitale.

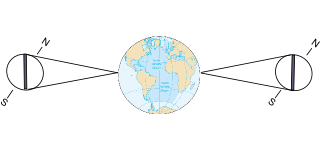L’observateur peut donc successivement observer, au cours de plusieurs lunaisons, les zones polaires Nord et Sud du globe lunaire. De façon imagée, la Lune semble faire « oui » de la tête.

c) Les librations parallactiques

Il s’agit d’un phénomène purement optique, dû aux positions respectives de la Lune et de l’observateur à la surface du sol.
En début de nuit, alors que la Lune se lève pour un observateur situé à l’équateur, celui-ci est plus favorablement positionné pour observer le bord oriental de la Lune. À l’inverse, en fin de nuit, il peut observer plus favorablement le bord Ouest de la Lune.

Cette parallaxe, d’une valeur d’environ 1°, est très difficile à exploiter en pratique : en effet, c’est lorsque leur effet géométrique est maximal (lever et coucher de Lune) que l’observation est rendue plus difficile, en raison de la lumière de l’aube et du crépuscule, et de l’épaisseur plus importante de l’atmosphère terrestre à travers laquelle se fait l’observation.

d) Les librations physiques

Il s’agit cette fois de véritables vibrations physiques de la sphère lunaire autour de sa position moyenne. Ces infimes vibrations (pas plus de quelques minutes d’arc) sont causées par l’attraction variable de la Terre sur la Lune, et ne sont pas perceptibles à l’œil nu. L’étude de ces oscillations est de la plus haute importance pour la détermination de la forme et de la structure interne de la Lune.

L’ensemble de ces phénomènes de libration au cours de lunaisons successives permet d’observer environ 59 % de la surface lunaire depuis la surface terrestre. Les zones supplémentaires ainsi offertes à l’observation sont très déformées par l’effet de perspective, et rendent difficile l’observation de ces régions depuis la Terre. Seules les sondes spatiales, par un survol régulier, en permettent l’étude topologique précise.

–

13) Nutation

La nutation est un mouvement périodique de l’axe de rotation d’un objet autour de sa position moyenne, qui s’ajoute à la précession.

La nutation a été découverte en 1748 par l’astronome britannique James Bradley (1693-1762) en observant l’étoile Gamma Draconis (Eltanin) en vue de déterminer sa parallaxe.

En raison de l’attraction conjuguée du Soleil et de la Lune, la nutation se traduit par une oscillation de l’axe de rotation de la Terre pouvant aller jusqu’à 17,2″ (secondes d’arc) avec une période de 18,6 ans, qui est égale à celle de la précession du nœud ascendant de l’orbite lunaire. Le pôle vrai dessine alors autour du pôle moyen une ellipse dont le grand axe mesurant 9,21″ est dirigé vers le point vernal.

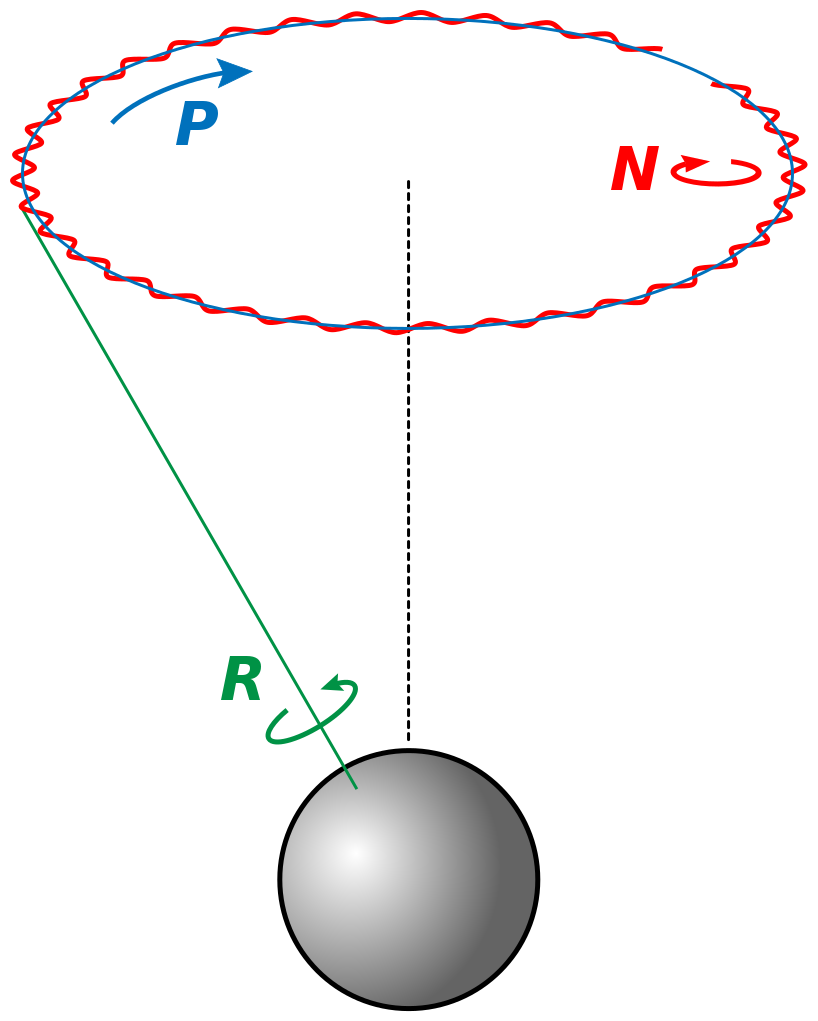
La rotation (vert), la précession (bleue) et la nutation en oblique (rouge) d’une sphère

Classiquement, la nutation est composée de deux éléments :

Nutation en longitude : décrivant l’oscillation du point vernal vrai autour du point vernal moyen. Au1^er janvier 2015, sa valeur angulaire était de 4,872″.

Nutation en obliquité : décrivant l’oscillation de l’équateur vrai autour de l’équateur moyen. Au 1^er janvier 2015, sa valeur angulaire était de -9,540″.

Les catalogues d’étoiles donnent habituellement les coordonnées astrométriques des étoiles. Celles-ci sont les coordonnées moyennes à une époque T fixée. Si on désire avoir les coordonnées vraies à une autre époque, on doit corriger ces coordonnées en tenant compte de la précession pendant la durée s’écoulant entre les deux époques, puis corriger ces coordonnées moyennes « corrigées » en ajoutant l’effet de la nutation.

–

14) Ondes gravitationnelles

Un article paru dans LE MONDE SCIENCE ET TECHNO | 11.02.2016

Les ondes gravitationnelles détectées un siècle après avoir été prédites

Un interféromètre servant à l’observation des ondes gravitationnelles (LIGO) le 8 février 2016

Énorme secousse dans le monde scientifique, pour une découverte majeure, à ranger au sommet des plus grandes percées de la connaissance. Pour la première fois, des vibrations venues de l’espace et d’une étrange nature ont été détectées sur Terre, confirmant une prédiction d’Albert Einstein vieille d’un siècle.

Ces tressautements, baptisés « ondes gravitationnelles », compriment et dilatent à la vitesse de la lumière l’espace-temps qui nous entoure, comme le son le fait avec l’air. « Ou comme du veau en gelée tremblote lorsqu’on le secoue », aime à dire Thibault Damour, spécialiste de la relativité générale à l’Institut des hautes études scientifiques de Bures-sur-Yvette (Essonne). L’espace-temps, c’est-à-dire la trame même du monde dans lequel nous vivons, est donc un contenant élastique, susceptible d’onduler à la manière des rides à la surface d’une eau perturbée par le lancer d’un caillou. La détection de ce premier clapotis cosmique est détaillée dans la revue Physical Review Letters du 11 février par l’équipe de l’instrument LIGO, aux Etats-Unis, en collaboration avec celles de Virgo, détecteur essentiellement franco-italien et construit près de Pise, et de GEO600, en Allemagne. « Cette détection est le début d’une nouvelle ère, celle de l’astronomie des ondes gravitationnelles devenue désormais une réalité », a lancé Gabriela Gonzalez, porte-parole de l’équipe LIGO, professeur d’astrophysique à la Louisiana State University.

Aboutissement

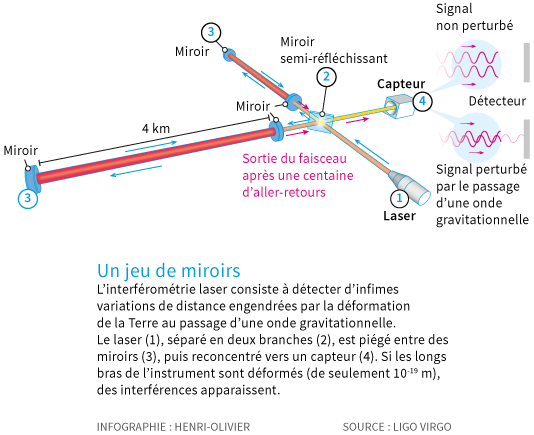
Les chercheurs ont repéré l’infime effet du passage d’une telle onde, qui a la capacité étonnante de distordre les distances, de les allonger ou de les réduire très légèrement. Aucune autre onde ne peut le faire. L’effet est faible, de l’ordre d’une variation du dix millième de la taille d’une particule élémentaire (environ 10^-19 m). Autrement dit, comme si l’étoile la plus proche, Proxima du Centaure, située à plus de quatre années-lumière de la Terre, se rapprochait de nous d’un demi-diamètre de cheveu… « Nous verrons enfin des choses jamais vues parce qu’elles n’émettent pas de lumière », souligne Pierre Binétruy, professeur à l’université Paris-VII Pour mesurer une si minuscule distance, les chercheurs ont construit depuis vingt ans des « amplificateurs » géants. LIGO est ainsi fait de deux tunnels perpendiculaires de quatre kilomètres de long chacun. A l’intérieur, deux faisceaux laser, parfaitement synchronisés entre eux, effectuent des dizaines d’allers-retours entre des miroirs. Puis, ces deux rayons sont recombinés à la sortie afin de vérifier leur synchronisation. Si une onde gravitationnelle secoue l’espace-temps et se propage jusque-là, elle étire un trajet lumineux avant l’autre, désynchronisant les lasers.

C’est ce qui s’est passé le 14 septembre 2015 à 11 h 51 (heure française) sur les deux sites américains jumeaux construits en Louisiane et dans l’Etat de Washington à 3 000 kilomètres de distance. Les « sismographes » se sont agités avec 7 millisecondes de décalage. « C’était trop beau pour être vrai ! », se souvient Jean-Yves Vinet, ancien responsable de Virgo (2007-2011), aujourd’hui directeur de recherche CNRS à l’Observatoire de la Côte d’Azur. Mais après des semaines de vérifications, écartant toute erreur, la confirmation est arrivée. « C’est l’aboutissement d’un très gros travail. C’est enthousiasmant », constate Eric Chassande-Mottin, chercheur CNRS du laboratoire Astroparticule et cosmologie.
Le signal enregistré par les chercheurs précise, en outre, l’origine de cette secousse, apportant une seconde découverte majeure. Il s’agit de la fusion de deux trous noirs en un nouveau, deux fois plus gros. Le duo est, respectivement, vingt-neuf et trente-six fois plus massif que le Soleil, et situé à plus d’un milliard d’années-lumière de la Terre.« C’est extraordinaire. Quand j’ai commencé ces travaux, dans les années 1970, les trous noirs n’étaient à peine qu’une hypothèse », se souvient Jean-Yves Vinet. Mieux, les chercheurs ont vu respirer ces géants d’où aucune lumière ni matière ne peuvent s’échapper. Lorsque les deux trous noirs se rapprochent, des ondes gravitationnelles sont créées, affolant périodiquement les détecteurs de LIGO. Puis, quand ils fusionnent, l’objet patatoïde qui en résulte n’adopte pas immédiatement une forme stable. Il vibre, telle une cloche, et fait trembler la gelée cosmique jusqu’aux détecteurs terrestres, d’une manière différente de la sarabande précédente. Un nouveau trou noir est en train de naître. « La masse finale du trou noir est 62 fois celle du Soleil. C’est moins que la somme des deux trous noirs; l’excédent a été converti en ondes gravitationnelles », indique Nicolas Arnaud (CNRS) du Laboratoire de l’accélérateur linéaire à Orsay.

C’est à ce spectacle et à bien d’autres que rêvent d’assister plus souvent les astronomes désormais. « Cela ouvre une grande période nouvelle et excitante. L’Univers est mû par la gravité, mais on ne l’observe qu’avec la lumière. Nous verrons enfin des choses jamais vues parce qu’elles n’émettent pas de lumière, estime Pierre Binétruy, professeur à l’université Paris-VII. Nous changeons d’époque. » « A chaque fois que nous braquons un nouvel instrument vers le ciel, on voit et on comprend des choses nouvelles. Ce fut le cas avec Galilée pointant sa lunette vers Jupiter et découvrant ses satellites », rappelle Jean-Yves Vinet.

↑ Une petite vidéo explicative de Futura Sciences sur les ondes gravitationnelles

Une nouvelle fenêtre astronomique

Seuls des événements impliquant de gros objets en mouvement peuvent faire osciller la gelée de veau cosmique. Comme des étoiles explosant en supernova; ou des étoiles mourant et se contractant en trou noir ou en étoiles à neutrons, appelées également « pulsars », qui condensent l’équivalent de la masse du Soleil sur seulement dix kilomètres de rayon; ou encore l’origine violente de l’Univers au moment du Big Bang, il y a plus de treize milliards d’années.

Cette première découverte ouvre donc une nouvelle fenêtre astronomique sur ces phénomènes, en élargissant le spectre des moyens d’observation après la lumière visible, les rayons X, infrarouges, ultraviolets, les ondes radio ou même les neutrinos (des particules quasiment sans masse qui interagissent peu avec la matière).

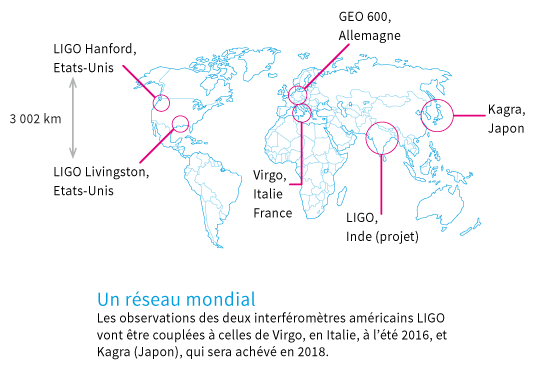
Pour la suite, Virgo fait actuellement peau neuve pour être aussi précis que son collègue américain et reprendre du service avant la fin 2016. Son couplage avec LIGO permettra une localisation précise des sources dans le ciel. Les Japonais achèvent Kagra; les Indiens comptent sur LIGO India. Et les chercheurs voient encore plus loin. Les instruments terrestres sont en effet limités à l’observation d’objets peu massifs et proches, toutes proportions gardées.

En effet, plus les « cailloux » agitant l’espace-temps sont gros, plus les crêtes des vagues créées sont éloignées et plus il faut des bras grands pour en saisir le passage. Des trous noirs, plusieurs millions de fois plus lourds que le Soleil, comme celui au cœur de notre galaxie, resteront en fait invisibles à LIGO et à Virgo.

Des rumeurs bruissent déjà sur le fait que le détecteur LIGO aurait d’autres secousses dans son sac. La suite consistera à installer en orbite eLISA, une sorte de triangle de faisceaux laser dont les « bras » d’un million de kilomètres de long bougeraient sous l’effet d’ondes gravitationnelles. Lancement prévu dans les années 2030. L’Agence spatiale européenne a mis sur orbite, le 3 décembre 2015, LISA Pathfinder, un satellite destiné à tester des technologies nécessaires à eLISA.

Cette détection d’ondes gravitationnelles, aussi compliquée soit-elle, n’est pas une surprise. La relativité générale est fiable et éprouvée depuis de nombreuses années : la plupart des phénomènes étranges prévus par cette théorie ont déjà été observés. Par exemple, les gros objets dévient les rayons lumineux, ce qui décale effectivement la position des étoiles dans le ciel. Ou bien une horloge bat plus vite le tempo en altitude qu’en surface (une information essentielle pour corriger les signaux GPS). Quant aux ondes gravitationnelles elles-mêmes, leur présence avait été repérée en 1978 et saluées par un prix Nobel en 1993 : la rotation de deux pulsars détectés en 1974 et se tournant autour s’accélérait à cause de l’émission d’ondes gravitationnelles entre les deux objets. En revanche, jamais ces ondes n’avaient été ressenties sur Terre. Des rumeurs bruissent déjà sur le fait que LIGO aurait d’autres secousses dans son sac.

S’il ne fait pas de doute qu’un prix Nobel couronnera cette découverte, les noms des lauréats seront difficiles à choisir. L’Américain Rainer Weiss, du MIT, est à l’origine, dans les années 1970, des premières études précises sur les défis à relever pour de futurs instruments. Kip Thorne, charismatique physicien américain, a poussé à la réalisation de LIGO dans les années 1990. Ronald Drever, un Ecossais, a eu l’une des idées-clés permettant d’augmenter la puissance des lasers. Côté européen, le Français Alain Brillet et l’Italien Adalberto Giazotto ont contribué largement aux techniques optiques et mécaniques nécessaires au fonctionnement parfait de Virgo. Et, bien sûr, les porte-parole de LIGO, Gabriela Gonzalez, ou de Virgo, Fulvio Ricci, sont aussi sur les rangs. De quoi secouer encore le landerneau scientifique.

Un siècle d’attente

Albert Einstein par sa double théorie de la relativité restreinte (1905) et générale (1915) a bouleversé les notions intuitives de temps, d’espace et d’énergie.

Selon la première théorie, la description complète et correcte de l’Univers ne doit pas séparer le temps et les positions dans l’espace mais les considérer ensemble : un point dans l’espace-temps est en fait un événement, c’est-à-dire une position attachée à un temps. Le temps absolu n’existe pas. Il dépend des vitesses relatives entre observateurs, par exemple. Une horloge qui se déplace affiche un temps qui s’écoule plus lentement qu’une autre immobile.

Une conséquence de la seconde théorie est que cet espace est structuré par la force de gravitation : les objets lourds courbent l’espace-temps, comme une boule s’enfonce dans un drap tendu. En retour, la structure de l’espace-temps force la matière et la lumière à suivre ses courbes. C’est dans cet espace élastique que nous vivons et que se propagent les ondes gravitationnelles qui distordent les distances, comme le son est une compression de l’air.

Une nouvelle détection d’ondes gravitationnelles a eu lieu le 14 août 2017 et a été publiée le 28 septembre 2017 :

Communication LIGO / VIRGO / NASA – 28 Septembre 2017
Nouvelle détection d’ondes gravitationnelles

Explication : De plusieurs endroits de la Terre trois détecteurs d’ondes gravitationnelles ont annoncé une détection conjointe d’ondulations dans l’espace-temps, le quatrième détecteur a annoncé la fusion de deux trous noirs dans l’Univers. L’évènement a eu lieu le 14 août 2017 et a été nommé GW170814, par les observatoires LIGO à Hanford (état de Washington) et Livingston (état de Louisiane) ainsi que le plus récent observatoire VIRGO près de Pise en Italie.

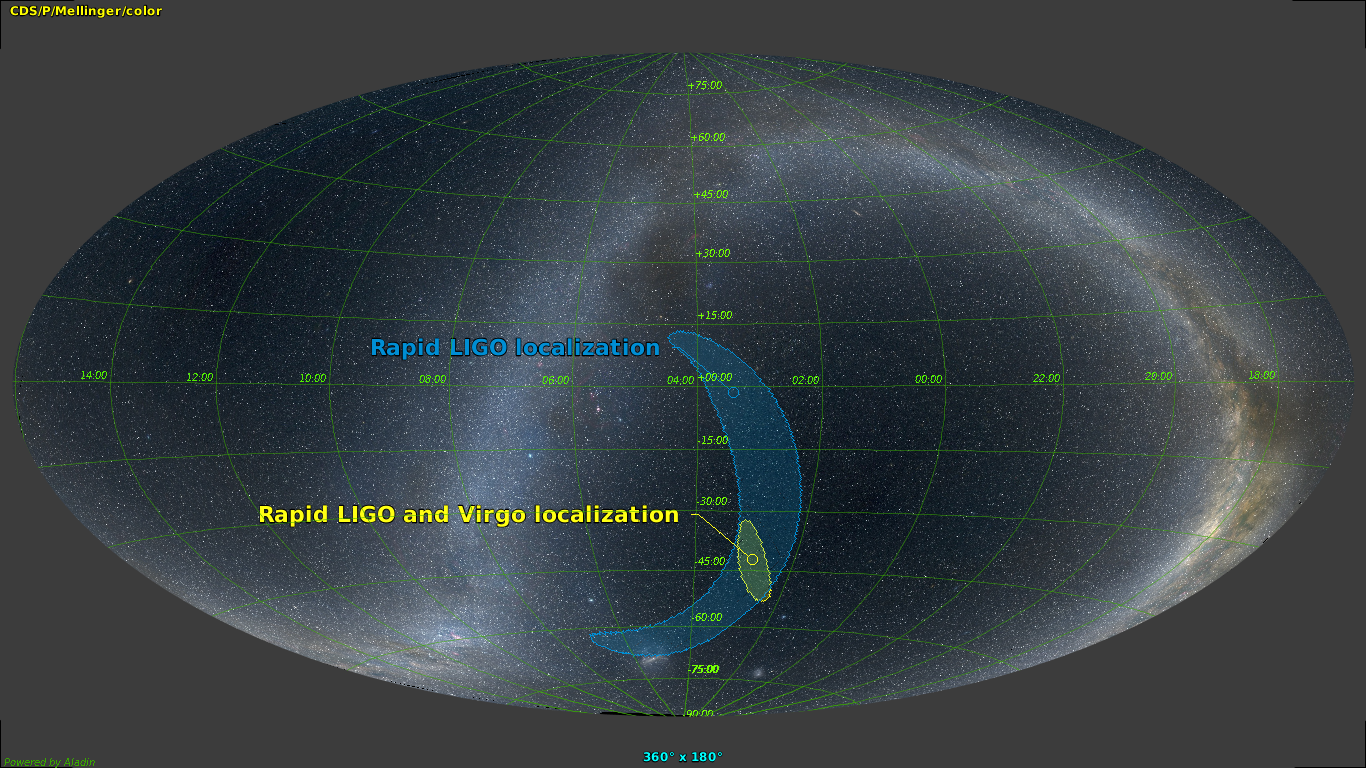
Le signal a été émis dans les ultimes moments de la fusion de deux trous noirs de respectivement 31 et 25 masses solaires, situés à environ 1,8 milliard d’années-lumière. En comparant les écart de temps des détections sur plusieurs sites éloignés a permis aux astronomes d’améliorer substantiellement l’endroit où cet évènement est arrivé dans le ciel. Juste au-dessus des nuages de Magellan, dans la direction de la constellation d’Eridan, qui a été la seule région possible compatible avec les mesures des 3 détecteurs (figurant en jaune sur cette carte du ciel).

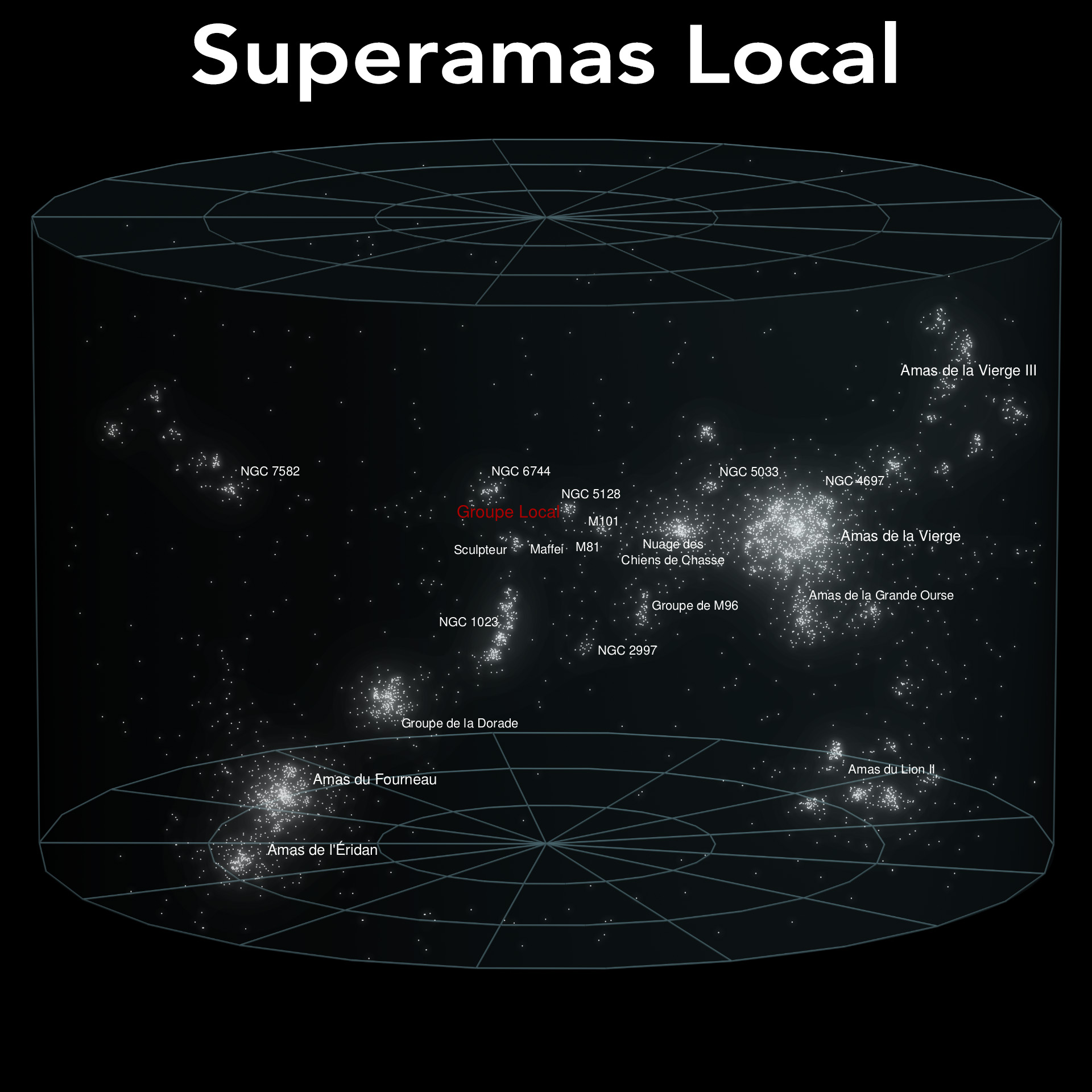
Cette projection totale du ciel inclut l’arc de notre Galaxie (la Voie Lactée). Une localisation améliorée de l’origine de ces ondes gravitationnelles a permis des observations rapides par d’autres observatoires utilisant des moyens plus conventionnels d’observation, analysant notamment les ondes électromagnétiques, à la recherche d’autres signaux en rapport avec l’évènement. L’apport du détecteur VIRGO a aussi permis de mesurer la polarisation de l’onde gravitationnelle, une propriété qui confirme les prédictions avancées par Einstein dans sa relativité généralisée en 1915.

–

15) Phémus

Les phémus sont des phénomènes mutuels qui ont lieu entre des satellites de Jupiter qui se croisent, s’éclipsent ou s’occultent. Les phénomènes peuvent être totaux, annulaires ou partiels. Tous les six ans, le plan orbital de la planète Jupiter et de ses satellites s’aligne avec notre ligne de visée terrestre. Ces phénomènes nous sont donc accessibles. On observe deux types de phémus : les éclipses et les occultations.


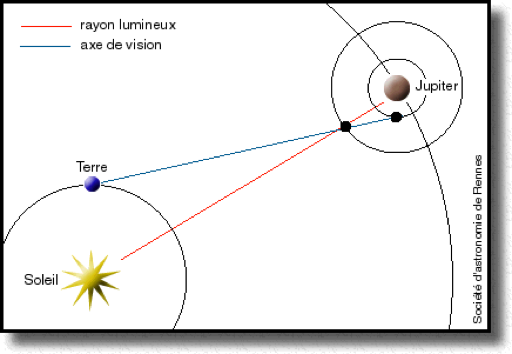Une éclipse	Une occultation

–

16) Planètes naines et petits corps (dénominations)

Termes : Cubewanos, Plutino ou Plutinien, Plutoïde, Sednoïde

Cubewano

Un cubewano est un membre d’une classe d’astéroïdes transneptuniens (dont l’orbite se situe au-delà de Neptune) évoluant dans la ceinture de Kuiper. Le nom a été dérivé du nom du premier objet de cette classe, (15760) 1992 QB₁. Les objets suivants de cette classe ont été d’abord nommés les QB1-os, puis cubewanos. En effet, QB-1, en anglais, se prononce /kju:bi wʌn/. Un cubewano est également appelé « objet classique de la ceinture de Kuiper » ou, en anglais, classical kuiper belt object (CKBO). Ce ne sont pas des objets en résonance avec Neptune dont ils restent à grande distance. Leurs orbites demeurent néanmoins stables car elles sont presque circulaires, à la manière des planètes : c’est cette similitude avec les planètes qui leur a donné le nom d’objets classiques de la ceinture de Kuiper. Leur rayon de révolution moyen est compris entre 42 et 48 ua. La théorie de leur formation est identique à celle des planètes, par accrétion lente de matière du disque protoplanétaire. Néanmoins, la faible densité de matière détectée dans cette région conduit certains scientifiques à imaginer une formation de ces objets plus proche du Soleil, suivie d’une migration à leur position actuelle, suite à la propre migration de Neptune.

Quelques représentants de cette famille :

(136472) Makémaké, probablement le plus gros cubewano (1.600 km) désormais classé comme planète naine et plutoïde;
(136108) Hauméa, autre planète naine et plutoïde (~1 500 km);
(15760) 1992 QB₁, premier objet transneptunien découvert depuis Pluton et Charon;
(20000) Varuna (900 km), premier gros planétoïde découvert dans la ceinture;
(50000) Quaoar, plus grand planétoïde connu jusqu’à la découverte de (90377) Sedna en 2003;
1998 WW₃₁, premier objet transneptunien binaire connu après le couple Pluton-Charon;
(58534) Logos, objet double puisque son satellite Zoé (64 km de diamètre) est presque aussi massif que ce planétoïde de 80 km de diamètre;
(88611) Teharonhiawako, planétoïde de 175 km de diamètre accompagné d’un satellite Sawiskera (109 km de diamètre);
(66652) Borasisi, planétoïde de 166 km de diamètre accompagné d’un satellite Pabu (137 km de diamètre).

Plutinos ou Plutiniens, ne pas confondre avec Plutoïdes :

Les plutinos (ou plutiniens) sont des objets transneptuniens, situés dans la ceinture de Kuiper, et qui sont en résonance 2:3 avec Neptune. Cela signifie qu’ils effectuent deux orbites autour du soleil pendant que Neptune en fait trois. De ce fait, et même s’ils croisent l’orbite de la planète géante, ils ne peuvent être éjectés gravitationnellement par celle-ci. Cette caractéristique étant partagée par Pluton, ces corps ont été nommés « plutinos » (c’est-à-dire « petits plutons »).

Les Plutoïdes sont des objets transneptuniens mais pas forcément en résonance 2:3 avec Neptune. Donc, attention, les plutinos ou plutiniens sont des plutoïdes mais l’inverse n’est pas vrai !!

Quelques représentants de cette famille :

(32929) 1995 QY₉: il croise l’orbite de Neptune sans jamais s’approcher de la planète. Cette particularité est partagée par un certain nombre d’autres membres de la famille des plutinos, dont Pluton;
(47171) 1999 TC₃₆: comme la paire Pluton-Charon, il s’agit d’un objet binaire;
(90482) Orcus considéré actuellement le plus grand si on excepte Pluton et sa plus grande lune Charon;
(28978) Ixion (759 km de diamètre) a détenu pendant quelques mois le record de taille des planétoïdes.

Sednoïde : Un sednoïde est un objet détaché dont le périhélie est supérieur à 75 unités astronomiques, dans ce qui est appelé le nuage d’Oort interne. La création de la catégorie des sednoïdes date de l’annonce de la découverte de 2012 VP₁₁₃ : il s’agit en effet du deuxième gros objet ayant un périhélie supérieur à 75 unités astronomiques, avec une orbite similaire à celle du premier objet de ce type connu, Sedna. Sedna a un périhélie à 76 UA (et un aphélie à 955 UA), 2012 VP₁₁₃ a un périhélie à 80,5 UA (et un aphélie à 445 UA).

La nouvelle classe regroupant ce genre d’objets a été nommée d’après Sedna car c’en était (et c’en est toujours à l’heure actuelle) le membre connu le plus important.

–

17) Précession des équinoxes

La précession des équinoxes est le lent changement de direction de l’axe de rotation de la Terre.

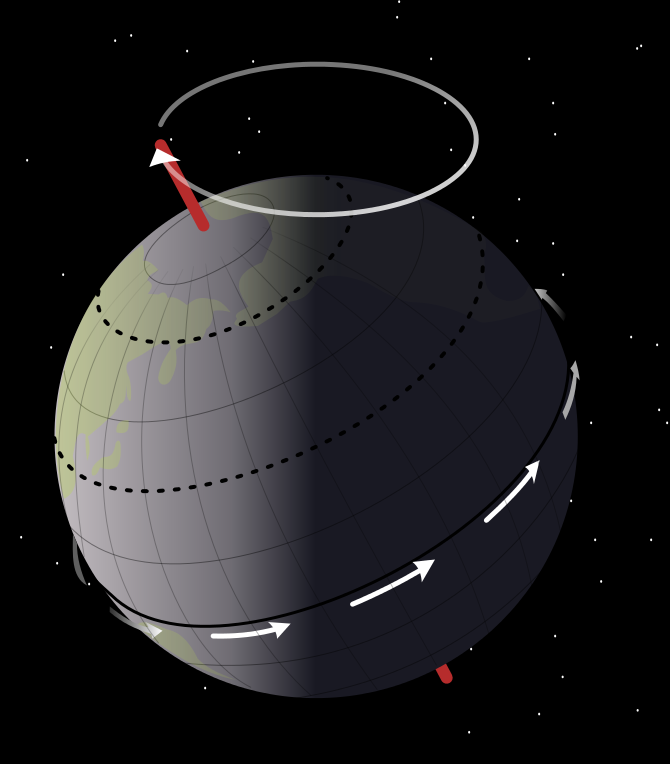
Ce changement de direction est provoqué par le couple qu’exercent les forces de marées de la Lune et du Soleil sur le renflement équatorial de la Terre. Ces forces tendent à amener l’excès de masse présent à l’équateur vers le plan de l’écliptique. La Terre étant en rotation, ces forces ne peuvent changer l’angle entre l’équateur et l’écliptique mais provoquent un déplacement de l’axe de rotation de la Terre dans une direction perpendiculaire à cet axe et au couple. Mises à part les petites perturbations agissant sur ce déplacement (par exemple la nutation), l’axe de la Terre décrit la surface d’un cône ou « entonnoir » d’axe perpendiculaire au plan de l’écliptique (portant dans l’espace la trace de la trajectoire de la Terre autour du soleil), à la manière de l’axe d’une toupie posée sur une table (qu’on voit tourner autour de la verticale).

Ce mouvement aboutit à déplacer l’orientation de l’axe des pôles par rapport aux étoiles, de sorte que, au fil des millénaires, l’étoile polaire (repérant à peu près la direction du nord géographique) ne soit plus toujours la même. Le mouvement de l’axe des pôles terrestres entraîne avec lui le plan de l’équateur (qui lui est perpendiculaire), et de ce fait le point vernal, ou point équinoxial, indiquant la direction du soleil à l’équinoxe de printemps) précède chaque année sa position antérieure sur l’écliptique, par rapport au sens de l’orbite Terrestre autour du soleil. Pour cette raison ce mouvement est appelé précession des équinoxes. Le point équinoxial effectue de la sorte, dans le sens contra rotatif (par rapport au sens de la rotation de la Terre autour du soleil), un tour complet de l’écliptique en 25 760 années environ, et l’axe de la Terre décrit durant ce même temps un cône complet.

Une des conséquences de ce déplacement est le changement de position des étoiles sur la sphère céleste dans le système de coordonnées équatoriales. Actuellement dans l’hémisphère Nord, l’étoile brillante la plus proche du pôle nord céleste (dont elle n’est distante que d’environ 1°) est α Ursae Minoris (m 1,97) dite aussi l’étoile polaire. Dans le passé, vers 3000 av. J.-C., c’était l’étoile α Draconis (Thuban) qui servait d’étoile polaire mais elle était beaucoup moins lumineuse que l’étoile polaire. Par contre, dans environ 8 000 ans Alpha Cygni (Deneb, 1,25^m) puis dans environ 12 000 ans, la très brillante Alpha Lyrae (Vega, 0,03^m) seront chacune à leur tour l’étoile polaire, avec cependant une erreur d’au moins 4 degrés. Dans l’hémisphère sud, les ciels nocturnes sont actuellement relativement dépourvus d’étoiles brillantes dans la région du pôle : l’étoile Sigma Octantis, quoique fort proche, est vraiment trop faible pour être visible (5,5^m). Dans environ 13 000 ans, ce sera au tour d’Eta Columbae (4^m) d’être au plus proche du pôle sud céleste, dont elle en est actuellement au plus éloigné.

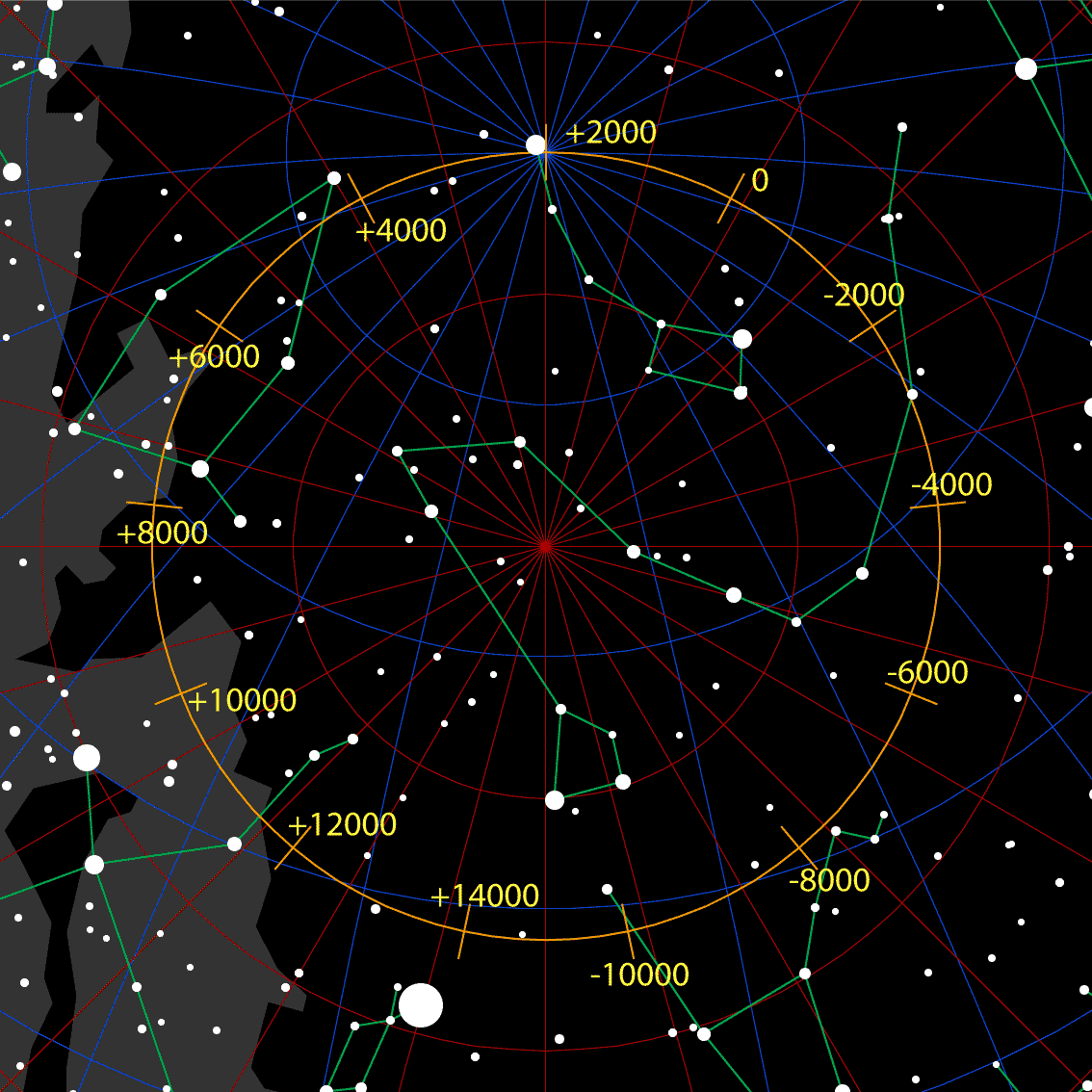
Trajet de l’axe du pôle Nord sur la voûte céleste, dû à la précession (en supposant une vitesse de précession et une obliquité constantes)

Comme l’orbite de la Lune est inclinée par rapport au plan de l’écliptique, l’action de la Lune vient légèrement perturber la précession en y ajoutant de petites oscillations dont la période est de 18,6 ans. Cet effet s’appelle la nutation (voir Nutation dans cette même page).

À cause de la précession des équinoxes, la durée du cycle des saisons (année tropique) est d’environ 20 minutes plus courte que le temps que met la Terre pour occuper la même position par rapport aux étoiles (année sidérale). Cette différence est importante pour les calendriers et leurs règles concernant les années bissextiles.

La valeur actuelle (en 2015) du déplacement est de 50,2912788082″ par an, soit environ 1° pour 72 ans. Toutefois la vitesse de précession n’est pas constante : actuellement elle est légèrement croissante avec le temps (elle valait par exemple 50,28796195″ par an en 2000 et 50,2901728435″ par an en 2010). Son accroissement séculaire est actuellement de 0,0221110852″. Mais ce terme d’accroissement n’est lui-même pas constant dans le temps, il varie avec une période d’environ 41 000 ans, la même durée que celle de la variation de l’obliquité de l’écliptique (un mouvement perpendiculaire à la précession), qui oscille entre 22° 2′ 33″ et 24° 30′ 16″. La valeur en l’an 2000 était de 23° 26′ 21,448″, la valeur actuelle (en 2015) est de 23° 26′ 14,427″ et continue de diminuer de ~46,8″ par siècle, soit tout de même de ~0,468″ par an. Sa valeur était précisément de 23° 30′ 00″ il y a 482 ans, soit en 1533. Dans une lettre de février 1464, l’astronome allemand Regiomontanus (Johannes Müller von Königsberg 1436-1476) reconnaît que les astronomes italiens Paolo Toscanelli (1397-1482) et Leon Battista Alberti (1404-1472) avaient déjà obtenu justement cette valeur lors de mesures annuelles faites durant les années 1440 à 1470 à Florence. Ces mesures ont été répétées avec une finesse accrue grâce au gnomon établi dès 1468 par Paolo Toscanelli à 90 mètres de haut dans la coupole (construite entre 1420 et 1436 par Filippo Brunelleschi) de la cathédrale Santa Maria del Fiore, permettant une remarquable précision de mesures de la hauteur du Soleil (et par conséquent de sa déclinaison) lors du solstice d’été à 2″ d’arc près, mesures possibles seulement entre le 20 mai et le 20 juillet. Pourtant, en 1588, Tycho Brahe dans son De mundi aetheri recentioribus phaenomenis, donne encore 23° 30′ 30″ qui était précisément la valeur de l’obliquité en 1469.

Histoire de la découverte du phénomène de précession

Le neuvième séminaire d’archéoastronomie organisé avec l’Observatoire Astronomique de Gênes, en Italie, le 31 mars 2007, a permis de faire le point des dernières découvertes concernant la mesure de l’équinoxe. La publication des actes montre que nos prédécesseurs avaient conçu dès la préhistoire des dispositifs permettant de mesurer l’équinoxe. Nos prédécesseurs démontrent qu’ils avaient les connaissances astronomiques pour comprendre et mesurer le phénomène : quelle que soit la latitude, la longitude et la déclinaison, et donc l’époque, le lever solaire d’équinoxe se fait toujours à l’azimut 90°.

Dans son livre Des Dieux, des tombeaux, des savants, l’archéologue C.W. Ceram signale que les astronomes babyloniens mentionnaient la précession des équinoxes même si, faute de modèle héliocentrique, ils n’en soupçonnaient pas la raison.

On croit que Hipparque avait découvert, aux environs de -130, le phénomène de la précession. En comparant ses mesures de la position de Alpha Virginis (Spica), une étoile proche de l’écliptique, par rapport au point vernal avec celles effectuées par les astronomes des siècles précédents, comme Timocharis d’Alexandrie et les astronomes babyloniens et chaldéens, il montra que le point vernal s’était déplacé de 2° par rapport à α Virginis. Il montra aussi que ce mouvement concernait aussi d’autres étoiles et valait au moins 1° par siècle.

Selon certains historiens, des civilisations antérieures à la Grèce antique connaissaient le mouvement de précession des équinoxes. Au début du XX^e siècle, l’allemand Schnabel attribua la découverte du mouvement à l’astronome babylonien Kidinnu et l’égyptologue René Adolphe Schwaller de Lubicz affirma que les anciens Égyptiens connaissaient cette précession. Ces affirmations sont cependant controversées. Une certaine confusion entre le phénomène observé et son explication persiste. Même sans témoignage explicite, il est raisonnable d’admettre que là où s’est transmise la tradition d’observer le ciel nocturne, à la longue on a dû constater un certain décalage dans la position des étoiles proches de l’écliptique aux moments notables de l’année (solstices et/ou équinoxes). De même si l’on s’est servi des étoiles éloignées des pôles pour orienter les monuments, après quelques siècles leurs alignements auront dévié. Toutefois ces exemples ne permettent pas d’affirmer que la précession a été connue car différentes explications sont possibles : soit que le mouvement du ciel (s’arrête et) s’inverse, soit que seules les étoiles des constellations zodiacales, mais non toutes, se meuvent à la manière des planètes.

Au XIII° siècle, Nasr Eddin Tusi avait calculé une valeur de 51″ par an pour la précession des équinoxes, ce qui est remarquable de précision.

Joseph-Alphonse Adhémar, James Croll et Milutin Milanković (1879-1958) ont eu le mérite de proposer une correspondance entre ces cycles astronomiques et leurs combinaisons, et les variations climatiques terrestres.

–

18) Quasi-satellites

En astronomie, un quasi-satellite (de l’anglais quasi-satellite) ou une quasi-lune (de l’anglais quasi-moon) est un astéroïde qui coorbite avec une planète autour du Soleil, sur une orbite elliptique qui lui est propre et dont l’excentrique est supérieure à celle de l’orbite de la planète, mais à la même longitude moyenne que celle de la planète. Vu depuis la planète, l’astéroïde semble réaliser une révolution autour d’elle sans pour autant être techniquement en orbite autour. Il s’agit donc d’un compagnon plus que d’un réel satellite naturel. Le mouvement d’un quasi-satellite est un exemple de mouvement coorbital caractéristique des objets en résonance 1:1 de moyen mouvement. Les deux autres types de mouvement coorbital sont l’orbite en têtard, caractéristique des astéroïdes troyens, et l’orbite en fer à cheval.

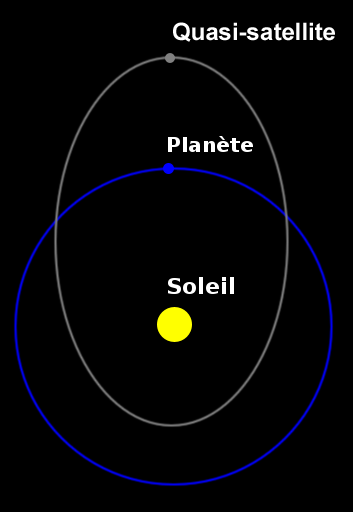Les quasi-satellites sont une solution particulière du problème astronomique des systèmes à trois corps. Il concerne donc deux objets en révolution autour d’un troisième plus massif (généralement une planète et un astéroïde autour d’une étoile) mais qui mettent cependant autant de temps pour parcourir leur orbite (résonance orbitale 1:1).

Il existe de nombreux exemples de résonance 1:1 dans le système solaire, comme les astéroïdes troyens placés aux points de Lagrange L4 et L5 de Jupiter, ou comme (3753) Cruithne, astéroïde compagnon de la Terre dont l’orbite paraît décrire un fer à cheval vue depuis cette dernière.


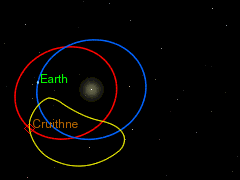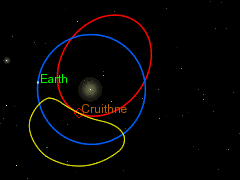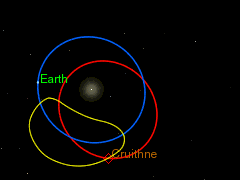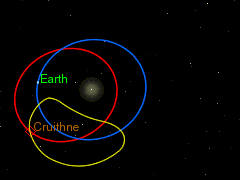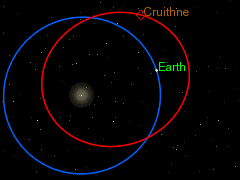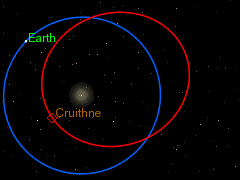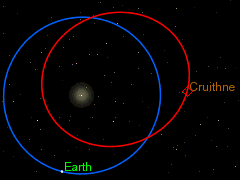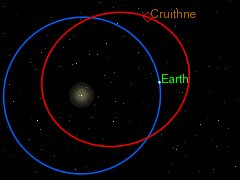Vue depuis la Terre, l’orbite de Cruithne a la forme d’un haricot.	Orbites héliocentriques de la Terre et Cruithne.

Cependant, à la différence de ces corps, les quasi-satellites semblent tourner autour de la planète qu’ils accompagnent pour un observateur situé sur celle-ci, accomplissant une sorte de révolution en autant de temps qu’il n’en faut à la planète pour en faire une autour de son étoile. Formellement, un quasi-satellite orbite autour de l’étoile et non pas autour de la planète comme un véritable satellite. Même si l’astéroïde reste relativement proche de celle-ci, il en est trop éloigné pour être lié gravitationnellement. Cependant, des perturbations gravitationnelles ont infléchi son orbite pour que, d’une part, il tourne autour de l’étoile en autant de temps que la planète (sur une orbite plus excentrique qui n’est pas forcément située dans le même plan) et, d’autre part, sur une orbite dont les grands axes ont à peu près la même orientation que celle de la planète. Quand l’astéroïde est au plus proche de l’étoile, il dépasse la planète. Comme son orbite est excentrique, il ralentit ensuite et s’éloigne et finit par dépasser l’orbite de la planète. Vu de celle-ci, tout se passe comme si, au long d’une année, l’astéroïde tournait peu à peu autour, décrivant une trajectoire qui n’est pas circulaire, ni même elliptique, mais en forme de haricot.

–

19) Rotation synchrone (généralement d’un satellite)

Un satellite est en rotation synchrone autour de sa planète quand son temps de révolution autour de sa planète est identique à son temps de rotation sur lui-même.

L’exemple que nous avons sous les yeux en permanence est celui de la Lune ! Elle met autant de temps à tourner autour de la Terre qu’à tourner sur elle-même. Conséquence : elle nous présente toujours sa même face. Depuis la terre on voit toujours le même côté de la Lune. Nous n’avons vu sa face “cachée” que grâce à des sondes qui ont été envoyées autour de la Lune pour en photographier l’autre face. Pourquoi en est-il ainsi ? C’est une conséquence des “forces de marée” (forces gravitationnelles mutuelles entre la Terre et la Lune) qui ont tendance à verrouiller les astres de cette façon.

Le verrouillage gravitationnel conduit la Lune à avoir un mouvement de rotation sur son axe en autant de temps que ce qu’elle met pour parcourir une orbite autour de la Terre. En dehors des effets de libration, cela mène la Lune à avoir toujours la même face orientée vers la Terre, comme montré sur l’animation de gauche (Lune montrée en vue polaire, dessin pas à l’échelle). Si la Lune ne tournait pas du tout sur elle-même, elle montrerait régulièrement sa face “avant” et sa face “arrière” lors d’une révolution, comme illustré sur l’animation de droite.

La rotation synchrone de la Lune n’est pas exceptionnelle dans le système solaire : tous les gros satellites des planètes du système solaire sont synchrones également. Mercure et Vénus n’ont pas de satellite, Mars en a deux tout petits.

Jupiter a 4 gros satellites dits “galiléens” qui sont en rotation synchrone : Io, Europe, Ganymède et Callisto. De plus, les 3 premiers sont en “résonance orbitale” : pendant que Ganymède fait un tour de Jupiter, Europe en fait deux et Io en fait quatre.

Saturne a également 7 gros ou moyens satellites synchrones : Titan, Rhéa, Japet, Dioné, Théthys, Encelade et Mimas (ces 2 derniers sont plutôt petits). Mais, plus extraordinaire, Saturne possède une dizaine de tout petits satellites synchrones (quelques kilomètres). Ici la taille du satellite est supplantée par la forte influence conjointe de la planète et des liens gravitationnels de ces mini-satellites avec certains anneaux.

Uranus a ses 5 plus gros satellites en rotation synchrone : Titania, Obéron, Umbriel, Ariel et Miranda.

Neptune n’a qu’un seul gros satellite, Triton, et il est en rotation synchrone (mais rétrograde, c’est à dire que contrairement à la plupart des satellites du système solaire, il tourne autour de sa planète dans le sens contraire du sens de rotation de sa planète).

La planète naine Pluton présente un cas très rare. Pluton et Charon (son plus gros satellite) sont en double rotation synchrone. Il n’y en a pas un qui tourne autour de l’autre comme c’est le cas généralement, mais ils tournent ensemble autour d’un point où il n’y a rien. C’est probablement dû au fait que Pluton a un diamètre qui n’est que le double de celui de Charon. Cet état de choses fait que sur Pluton on verrait toujours la même face de Charon et inversement. De plus, dans le ciel de Pluton (quand on est du bon côté) Charon est toujours à la même place dans le ciel… et inversement quand on est sur Charon. D’ailleurs les astronomes d’aujourd’hui ont tendance à dire que Pluton n’a pas un satellite, Charon et 4 autres petits, mais que Pluton-Charon est une planète naine double avec 4 petits satellites.

La rotation synchrone est parfaitement possible entre une étoile et une planète. Dans le cas de Mercure on n’en est pas loin puisque le temps de rotation de Mercure sur elle-même (58,64 jours) est très exactement des 2/3 de son temps de révolution (87,97 jours) autour du Soleil. On appelle cela une résonance 2:3.

Le cas de Vénus est aussi troublant,mais dans ce cas on est passé au-delà : Vénus tourne sur elle-même plus lentement (en 243 jours) que le temps de son orbite autour du Soleil (224,7 jours). Dans le cas de Vénus, il n’y a pas de résonance.

La rotation synchrone planète/étoile a été détectée dans le cas de trois exoplanètes, parmi les 7 planètes en orbite autour de la même étoile Trappist-1 (nom officiel : 2MASS J23062928-0502285). Les planètes Trappist-1b, Trappist-1c et Trappist-1d sont en rotation synchrone autour de leur étoile, une petite naine rouge “froide” à 40 années-lumière de notre Soleil.

De plus la rotation synchrone a d’autres effets : le satellite présente toujours sa même face à sa planète mais, vu d’un autre angle ces satellites on toujours la même face tournée vers l’avant de leur déplacement et donc aussi, à l’opposé, la même face arrière. On appelle cela les hémisphères avant et arrière :

Hémisphère avant, hémisphère arrière : Cette dénomination pourrait n’avoir aucun sens dans l’espace, mais elle est due à la nécessité de préciser dans le cas de Saturne et d’autres planètes, l’orientation de certains satellites. En anglais, on parle de « leading » hemisphere et de « trailing » hemisphere. Cela ne s’applique qu’aux satellites synchrones qui tournent sur eux-même dans le même temps qu’ils effectuent une orbite autour de leur planète. En conséquence ils présentent toujours la même face à leur planète-mère. Ici la notion d’hémisphère avant décrit la face du satellite (toujours la même) qui est tournée vers la direction de son orbite, donc vers l’avant de sa course. C’est donc celle qui est la plus exposée à recevoir de la matière.

Cet état de fait est particulièrement marqué sur un satellite de Saturne, Japet, dont les différences de couleur entre les faces avant et arrière sautent aux yeux. Japet reçoit de grandes quantités de poussières sombres en étant proche du gigantesque anneau de Phœbé et à cause aussi du satellite Phœbé qui ramasse aussi ces poussières mais en perd une partie le long de l’orbite de Japet.

Photo de Japet par la sonde Cassini. On voit nettement sa face avant maculée de poussières sombres

–

20) Saturne : précisions sur les divisions et les “annelets” de la planète

Divisions et lacunes : auparavant, les séparations qui se trouvent entre les anneaux de Saturne étaient toutes appelées « divisions ». Maintenant, on distingue les « divisions » (qui font généralement 1.000 km de large ou plus), alors qu’on nomme désormais « lacunes » des petites divisions qui font 500 km de large ou moins. A l’heure actuelle il y a dans les anneaux de Saturne 4 divisions et 14 lacunes.

Anneaux et annelets : les annelets sont de tout petits anneaux très fins que l’on trouve généralement dans les divisions ou les lacunes des anneaux de Saturne. De plus, ils semblent être d’une nature différente des anneaux en ce sens qu’ils semblent souvent être spiralés et qu’ils ont parfois des orbites plus excentriques que les anneaux. Ils sont souvent en interaction avec des très petites lunes de Saturne. Les anneaux et les annelets échangent fréquemment de la matière avec de petits satellites voisins et cela fonctionne dans les deux sens : le satellite prend de la matière à l’annelet ou, au contraire lui en donne. A ce jour on recense 13 anneaux sur Saturne et des milliers d’annelets.

–

21) Tholins

Le tholin (du grec ancien θολός / tholós, « encre de seiche », en référence à l’aspect et à la couleur), ou la tholine (le genre n’est pas fixé par l’usage), est une substance organique plus ou moins azotée de masse moléculaire élevée (~ 8 kDa), de couleur rouge brun (sépia) et de structure mal connue, qu’on trouve à la surface de nombreux astres du Système solaire externe. Le tholin est composé de molécules diverses, ce qui fait qu’on l’écrit également au pluriel : les tholins, les tholines, en référence aux composés ou aux molécules qui le constituent (toutes ces formes lexicales se rencontrent dans la littérature francophone).

Les mécanismes exacts de la formation du tholin ne sont pas connus, mais il s’en forme sous l’action du rayonnement ultraviolet sur des composés organiques simples, tels que des hydrocarbures légers (méthane CH₄, éthane C₂H₆, éthylène C₂H₄, etc.), en présence d’azote N₂ et/ou d’eau H₂O.

On ne trouve pas de tholin à la surface de la Terre mais on en trouve au contraire en abondance sur les satellites des planètes géantes, ainsi que, sans doute, sur les planètes naines et les petits corps du Système solaire. On en a également détecté dans le système stellaire de l’étoile binaire HR 4796 à l’aide de l’instrument NICMOS du télescope spatial Hubble. Généralement de couleur rouge-brun, le tholin a une structure moléculaire difficile à caractériser car les résidus sont essentiellement insolubles.

Les tholins de Titan et de Triton, satellites respectivement de Saturne et de Neptune, sont des substances organiques riches en azote du fait de l’action des ultraviolets sur des mélanges d’azote N₂ et de méthane CH₄ : l’atmosphère de Titan est en effet composée d’azote avec 1,4 % de méthane dans la stratosphère, taux qui augmente en se rapprochant du sol pour atteindre 4,9 % en dessous de 8 km d’altitude, où on trouve également des traces d’autres hydrocarbures légers tels que l’éthane C₂H₄, le diacétylène C₄H₂, le méthylacétylène C₄H₄, l’acétylène C₂H₂ et le propane C₃H₈, ainsi que du cyanoacétylène HC₃N, du cyanure d’hydrogène HCN et divers autres gaz; l’atmosphère de Triton, quant à elle, est un peu moins bien connue et semble composée essentiellement d’azote N₂ avec des traces de méthane CH₄. A contrario, le tholin « de glace » résulte de l’irradiation de clathrates de méthane CH₄ et d’éthane C₂H₆ dans de la glace d’eau et est donc dépourvu d’azote; le plutino Ixion serait particulièrement riche en ce genre de composés.

–

22) Point vernal, ascension droite, déclinaison, coordonnées équatoriales

Le point vernal, c’est quoi ?

Sur la sphère céleste, l’équateur céleste et l’écliptique se croisent. Les deux intersections sont appelées des nœuds. Au cours de son mouvement apparent, le Soleil croise ces deux points, l’un en passant de l’hémisphère Nord à l’hémisphère Sud, c’est le nœud descendant; l’autre en passant de l’hémisphère Sud à l’hémisphère Nord, c’est le nœud ascendant. Ce dernier est le point vernal (noté γ, parfois g), parfois noté point de l’équinoxe vernal ou point de l’équinoxe de printemps.

Le point vernal est la base du système de coordonnées équatoriales. Les références sont d’une part le méridien passant par le point vernal, il définit le méridien zéro pour la mesure des ascensions droites, et d’autre part l’équateur céleste à partir duquel la déclinaison est mesurée (positivement au-dessus de l’équateur, négativement en dessous). Les coordonnées du point vernal sont l’ascension droite (α) = 0 h (étant situé sur le méridien zéro) et sa déclinaison (δ) est nulle (étant situé sur l’équateur céleste).

Le système de coordonnées équatoriales est donc un système de coordonnées célestes dont les valeurs sont indépendantes de la position de l’observateur. Ce système utilise comme plan de référence la projection, sur la sphère céleste, de l’équateur de la Terre. Cette projection est l’équateur céleste, qui divise le ciel en deux hémisphères, chacun ayant comme axe de référence la projection d’un pôle terrestre, perpendiculaire à l’équateur céleste. À partir de ces divisions, le système permet d’établir deux coordonnées angulaires : l’ascension droite et la déclinaison.

L’ascension droite ( $α, alpha$ ) est l’angle mesuré sur l’équateur céleste à partir d’un point de référence, le point vernal, correspondant à une intersection entre l’équateur céleste et l’écliptique. À partir de ce point, l’angle est mesuré vers l’Est et comporte 24 divisions principales de 15 degrés (°) chacune, nommées « heures ». Chacune des heures se divise en minutes et en secondes.

La déclinaison ( $δ, delta$ ) est l’angle mesuré perpendiculairement entre l’équateur céleste et l’objet céleste observé. Elle se mesure en degrés, positifs pour les objets situés dans l’hémisphère nord et négatifs pour ceux de l’hémisphère sud. La déclinaison varie ainsi de -90° (pôle sud) à +90° (pôle nord) en passant par 0° à l’équateur céleste.

L’ascension droite et la déclinaisons sont les équivalents astronomiques de la longitude et de la latitude.

↑ Coordonnées équatoriales

En astrologie, ce point porte le nom de « premier point du Bélier », d’après le nom de la constellation dans laquelle il se trouvait dans l’Antiquité. Toutefois, à cause de la précession des équinoxes, ce point se déplace lentement le long de l’écliptique. Le point vernal est actuellement situé dans la constellation des Poissons, il y est entré vers -60 et en ressortira vers 2600 pour entrer dans la constellation du Verseau.

Détermination du point vernal

Le point vernal étant défini comme le croisement de l’écliptique et de l’équateur céleste, il change de position avec les mouvements de précession et de nutation de l’axe de rotation de la Terre. Ces paramètres sont déterminés par l’International Earth Rotation and Reference Systems Service (IERS) en combinant les données fournies par un réseau de surveillance mondial. En raison des mouvements du point vernal, ce sont ses coordonnées J2000.0, c’est-à-dire au 1^er janvier 2000 à midi UTC, qui servent de référence pour le système de coordonnées équatoriales.

Précession des équinoxes

L’axe autour duquel la Terre tourne sur elle-même est l’axe des pôles terrestres, qui est de biais par rapport au plan de l’écliptique (voir le schéma ci-dessus). Mais en raison de la précession des équinoxes, cet axe des pôles trace lui-même au niveau de son pôle Nord très lentement un cercle dans l’espace, entraînant (du fait de l’angle de 90° avec l’équateur terrestre) un mouvement (durant ~ 260 siècles) du point vernal à rebours sur l’écliptique. Le point vernal, origine des douze signes astrologiques, met de l’ordre de 25760 ans pour remonter à reculons les douze constellations du zodiaque.

Nomenclature du point vernal

Le point vernal moyen (ou équinoxe moyen) à une époque “T”, est le nœud ascendant de l’écliptique moyen sur l’équateur moyen. Il est déduit à partir du point vernal relatif à une autre date par la précession des équinoxes.

Le point vernal vrai (ou équinoxe vrai) à une époque “T”, est le nœud ascendant de l’écliptique moyen sur l’équateur vrai. Il est déduit à partir du point vernal moyen par la nutation.

Conséquences du déplacement du point vernal :

Ce point vernal, et son déplacement dans le temps à rebours le long du zodiaque étaient connus dès l’antiquité. L’astronome, mathématicien et géographe grec Hipparque (~ 190 / ~ 120 av. J.C) avait, peut-être à la suite de certains babyloniens et chaldéens, constaté ce mouvement de précession et il l’avait même chiffré (avec une grosse erreur toutefois). Le déplacement du point vernal est mentionné dans divers textes religieux comme la Bible, puis que l’on y parle de l’« ère des poissons » comme devant commencer entre – 60 et 0 avant JC pour se terminer entre 2100 et 2600, date à laquelle commencera l’ère du Verseau, etc. En effet, le mouvement de précession étant étalé sur 25.760 ans, il faudrait 2146 ans pour que le point vernal change de signe zodiacal (sur la base de 12 signes égaux en angle de 30°, ce qui ne correspond d’ailleurs pas à la réalité, en raison de la largeur angulaire variable des constellations du zodiaque).

Un individu, né par exemple le 10 avril en 500 av JC est placé sous le signe du bélier (ce qui est toujours le cas dans l’astrologie actuelle). Par contre, né le 10 avril en 1600 après JC il serait réellement placé sous le signe des poissons en raison de la précession des équinoxes qui fait qu’à cette date, le soleil est devant la constellation des poissons. Un autre individu qui naîtra le 10 avril 2700 sera placé sous le signe du verseau pour les mêmes raisons, etc. Pour qu’un individu né à cette date du 10 avril puisse être, à nouveau, du signe du bélier, il faudra attendre environ les années (- 2200 à -60) + 25.760 = entre 23.560 et 25.700 !!!

Si l’astrologie explique que la place du soleil dans une constellation le jour de votre naissance détermine votre caractère ou votre destin, on s’éloigne radicalement de la réalité astronomique puisque les signes du zodiaque relatifs à votre horoscope sont figés dans le temps astrologique et ne suivent pas la réalité des choses telles que prouvées par l’astronomie. Donc les conclusions que les astrologues tirent de la soi-disant position du soleil dans une constellation le jour de votre naissance sont donc nécessairement erronées et le seront de plus en plus au cours de quelques 23.500 années à venir. La position des planètes dans les constellations ainsi que leur influence dans votre horoscope subissent exactement les mêmes erreurs fondamentales, puisque l’astrologie reste campée sur un dogme immuable, celui du ciel tel qu’il était à l’âge de l’antiquité gréco-romaine, celle du point vernal dans le Bélier. Notons aussi que les astrologues ne prennent en considération que 12 constellations dans le zodiaque au lieu des 13 qui y figurent. Par définition une constellation appartient au zodiaque si elle est traversée par l’écliptique. Or c’est aussi le cas de celle, oubliée (?) par les astrologues, Ophiuchus, appelée aussi le Serpentaire, entre le Scorpion et le Sagittaire.

Pour plus de précisions, voir notre document pdf “Les controverses du zodiaque“

–

23) Aurores polaires

Phénomène céleste hypnotique et fantasmatique, les aurores polaires sont provoquées par le vent solaire.

Une aurore polaire (également appelée aurore boréale dans l’hémisphère nord et aurore australe dans l’hémisphère sud) est un phénomène lumineux caractérisé par des voiles extrêmement colorés dans le ciel nocturne, le vert étant prédominant.

Elles sont le signe d’une perturbation du champ magnétique terrestre par le vent solaire. La Terre est en effet enveloppée d’un bouclier magnétique (la magnétosphère) qui lui sert de protection. Celui-ci se déforme sous l’effet de ces flots de matière expulsés par le Soleil, à la manière d’une grosse bulle de savon exposée en plein vent. Provoquées par l’interaction entre les particules chargées du vent solaire et la haute atmosphère, les aurores se produisent principalement dans les régions proches des pôles magnétiques, dans une zone annulaire justement appelée « zone aurorale » (entre 65 et 75° de latitude). En cas d’activité magnétique solaire intense, l’arc auroral s’étend et commence à envahir des zones beaucoup plus proches de l’équateur. L’aurore polaire due à l’éruption solaire de 1859 est « descendue » jusqu’à Honolulu et jusqu’à Singapour en septembre 1909 atteignant ainsi le dixième degré de latitude sud. En octobre et novembre 2003, une aurore boréale a pu être observée dans le sud de l’Europe, mais les régions les plus concernées par ce phénomène restent le Groenland, la Laponie, l’Alaska, l’Antarctique, le nord du Canada et l’Islande. Un phénomène d’ampleur exceptionnelle s’est produit le 24 octobre 2014, visible en Amérique du Nord et en Europe du Nord. Les aurores boréales sont également observables au nord de la Suède et de la Finlande, ainsi que dans les îles Shetlands au nord du Royaume-Uni.

Formation

Lors d’un orage solaire accompagnant un orage magnétique, et faisant suite à une éruption chromosphérique ou un sursaut solaire important (le soleil offre un pic d’activation solaire sur un cycle de 11 ans), un afflux de particules chargées, éjectées par le Soleil, entre en collision avec le bouclier que constitue la magnétosphère. Des particules électrisées à haute énergie peuvent alors être captées et canalisées par les lignes du champ magnétique terrestre du côté nuit de la magnétosphère (la queue) et aboutir dans les cornets polaires. Ces particules, électrons, protons et ions positifs, excitent ou ionisent les atomes de la haute atmosphère, l’ionosphère. L’atome excité ne peut rester dans cet état, et un électron change alors de couche, libérant au passage un peu d’énergie, en émettant un photon (particule élémentaire constitutive de la lumière visible). Comme la nature de ces ions (oxygène, hydrogène, azote, etc.) dépend de l’altitude, ceci explique en partie les variations de teintes des nuages, draperies, rideaux, arcs, rayons… qui se déploient dans le ciel à des altitudes comprises entre 80 et 1 000 km. L’ionisation résultant de cet afflux de particules provoque la formation de nuages ionisés réfléchissant les ondes radio.

Couleurs des aurores polaires

Les phénomènes auroraux prennent plusieurs teintes différentes, passant du vert au rose, au rouge et à l’indigo violet. L’étude spectrographique de la lumière émise montre la présence de l’oxygène (raie verte à 557 nm et doublet rouge à 630 et 636 nm) entre 120 et 180 km d’altitude, de l’azote et de ses composés et de l’hydrogène (656 nm) lors des aurores à protons. Aux plus basses altitudes, la couleur observée le plus fréquemment est le pourpre (altitudes de 90 à 100 km).

L’excitation des molécules, atomes et ions d’azote et d’oxygène sont à l’origine des principales couleurs. L’oxygène émet principalement du vert et du rouge, tandis que l’azote émet du bleu, du rouge et du violet. L’atmosphère a des densités en oxygène et en azote qui varient avec l’altitude, l’oxygène devenant plus dense que l’azote au-dessus de 200 km d’altitude, ce qui explique en partie la prédominance de vert dans les aurores polaires. Excitées, certaines des molécules de diazote interagissent aussi avec l’oxygène, causant une émission additionnelle de vert, ce qui contribue également à la dominance de la couleur verte. L’hélium et l’hydrogène produisent des aurores mauves ou bleues. Enfin, l’énergie du vent solaire joue aussi un rôle dans les couleurs observées.

Aurores polaires ailleurs que sur la Terre

Les aurores polaires ne sont pas un phénomène spécifique à la Terre. Il est possible d’en trouver sur n’importe quelle planète possédant un champ magnétique. Elles sont observables, entre autres, grâce aux photographies prises en ultraviolet par le télescope Hubble.

Les aurores polaires vues sur les planètes autres que la Terre peuvent être générées par d’autres phénomènes physiques que ceux provoquant les aurores terrestres. Sur Jupiter, par exemple, l’ovale auroral principal est une conséquence de la « rupture de co-rotation » du plasma : le champ magnétique de la planète entraîne normalement le plasma avec lui, mais, à partir d’une certaine distance, la vitesse à communiquer au plasma devient trop grande et celui-ci ne suit plus. Cela crée un courant électrique à l’origine de l’ovale auroral.

Sur Jupiter, les satellites de la planète créent un courant électrique en se déplaçant par rapport au champ magnétique (même phénomène que pour une dynamo). Ces courants créent des « spots auroraux », vus pour la première fois en infrarouge, puis en UV. On peut voir ces spots sur l’image ci-dessus, en dehors de l’ovale principal : le spot le plus brillant correspond à Io (à gauche), ceux de Europe et Ganymède sont visibles au premier plan.

Toujours sur Jupiter, un groupe de chercheurs du Laboratoire de physique atmosphérique et planétaire a été en mesure de faire l’observation de phénomènes auroraux sur la géante gazeuse par le biais du télescope Hubble. En particulier celles dues aux satellites Io, Europe et Ganymède. Leur travail révèle le détail des spots ultraviolets et permet une meilleure compréhension des phénomènes les engendrant.

Des aurores polaires ont également été photographiées par Hubble sur Saturne et d’autres par Mars Express sur la planète Mars grâce à l’instrument SPICAM (Mars ne possédant pas de champ magnétique global, ces aurores sont localisés dans des zones où subsiste un champ magnétique local). Des aurores polaires ont également été détectées sur Vénus, Uranus et Neptune.

Le 21 janvier 2013, des chercheurs annoncent avoir très probablement détecté pour la première fois des aurores sur des exoplanètes, grâce au Low-Frequency Array radio telescope basé aux Pays-Bas.

–

24) Le Diagramme de Hertzsprung-Russell

En astronomie, le diagramme de Hertzsprung-Russell, en abrégé diagramme H-R, est un graphe dans lequel est indiquée la luminosité d’un ensemble d’étoiles en fonction de leur température effective. Ce type de diagramme a permis d’étudier les populations d’étoiles et d’établir la théorie de l’évolution stellaire.

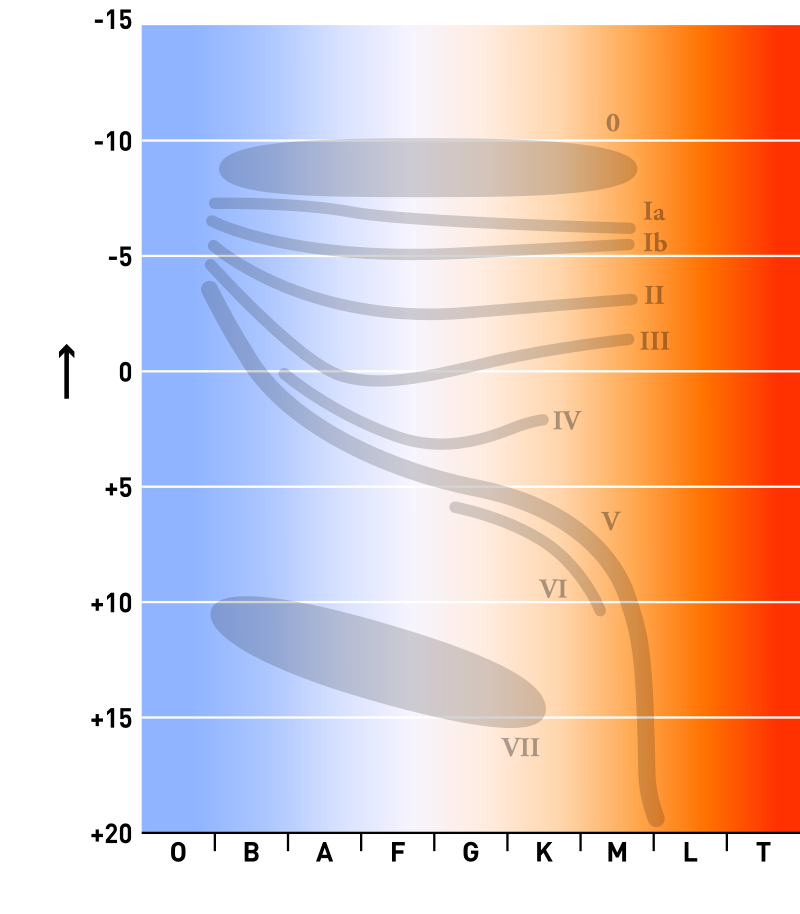
Origine : Le diagramme de Hertzsprung-Russell a été inventé autour de 1910 par Ejnar Hertzsprung et Henry Norris Russell.

Hertzsprung est un astronome danois (1873 – 1976). Il eut l’idée en 1905 de classer les étoiles d’un même type spectral en plusieurs classes de luminosité en fonction de leur température de surface. Pour des raisons historiques l’axe des températures est orienté vers la gauche. Le diagramme auquel il aboutit fut perfectionné par H. N. Russell.

Russell est un astronome américain (1877 – 1957), à qui l’on doit de nombreux travaux sur la physique des étoiles, qui l’amenèrent à établir une classification des étoiles en fonction de leur luminosité et de leur type spectral.

Définitions : Un diagramme de Hertzsprung-Russell représente soit la luminosité intrinsèque en fonction de la température (utilisée par les théoriciens), soit la magnitude absolue en fonction de l’indice de couleur (ce qui découle immédiatement de données photométriques). Dans ce second cas, on parle aussi de diagramme couleur-magnitude.

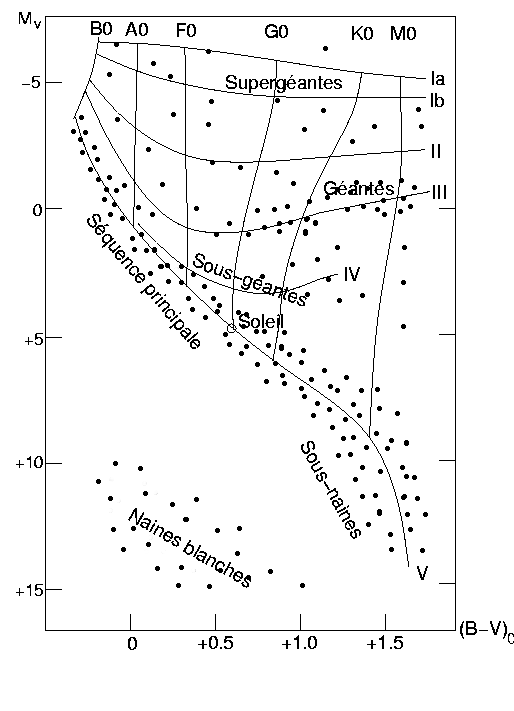
Un diagramme de Hertzprung-Russell est toujours présenté de la manière suivante :

la luminosité est en ordonnée, le plus brillant étant en haut ;
la température effective, ou l’indice de couleur, est en abscisse, le plus chaud étant à gauche.

De telles conventions viennent du fait que les premiers diagrammes étaient des diagrammes couleur-magnitude, qui montraient les données photométriques brutes issues de l’observation de populations stellaires : la magnitude d’un filtre en fonction de la différence de magnitude avec un autre filtre.

La classification spectrale des étoiles apparaît nettement sur le diagramme de Hertzsprung-Russell : les lignes presque verticales séparent les différents types spectraux, tandis que les lignes obliques ou presque horizontales sont appelées classes de luminosité. La figure ci-dessus illustre la classification.

L’ordre des lettres OBAFGKM du type spectral en ordonnée peut être retenu par la phrase mnémotechnique : “Oh Be A Fine Girl, Kiss Me!” (Oh, soit une gentille fille, embrasse-moi). On va de la classe O, qui est celle des étoiles très jeunes, bleues et extrêmement chaudes, jusqu’à la classe M qui, au contraire, est celle d’étoiles « vieilles », rouges et bien moins chaudes. Le Soleil est une étoile de type G2, donc une étoile jaune, en milieu de vie.

L’examen d’un diagramme d’une population d’étoiles, comme ci-dessous, montre une énorme concentration d’étoiles le long d’une diagonale ainsi qu’une concentration significative quelques magnitudes au-dessus de la diagonale. D’autres zones du diagramme sont complètement vides d’étoiles, ou très peu peuplées.

La séquence principale

C’est la région du diagramme de Hertzsprung-Russell où la majorité des étoiles résident, elle correspond à la diagonale allant du coin supérieur-gauche (chaud et lumineux) au coin inférieur-droit (froid et peu lumineux). Si la concentration d’étoiles y est si élevée, c’est parce que celles-ci y passent environ 90 % de leur vie en évoluant très peu, brûlant l’hydrogène en leur cœur.

La dispersion des étoiles autour de la séquence principale a plusieurs raisons. La composition chimique change légèrement la place de l’étoile sur le diagramme : plus celle-ci est riche en métaux, plus elle est froide et moins elle est lumineuse, car elle garde un rayon constant. Les étoiles de population II, beaucoup plus pauvres que les étoiles de population I, forment ainsi la classe des sous-naines. De plus, les étoiles accroissent lentement leur luminosité et changent de température pendant leur phase sur la séquence principale. D’autres facteurs comme la rotation, la présence de compagnons proches ou de champs magnétiques peuvent également expliquer un placement un peu dispersé. Un autre facteur est l’incertitude des observations; ces incertitudes affectent principalement la distance de l’étoile en question mais concerne aussi les étoiles binaires, non ou mal identifiées en tant que telles.

Les géantes

Environ 5 à 10 magnitudes au-dessus de la séquence principale, on trouve une importante concentration d’étoiles : il s’agit d’étoiles en fin de vie, soit au stade de géante rouge, avec une fine couche d’hydrogène qui « brûle » autour d’un noyau d’hélium inerte, soit, et surtout en fait, des étoiles de la branche horizontale, au cœur desquelles l’hélium fusionne pour donner du carbone et de l’oxygène. La combustion de l’hélium est cependant beaucoup plus rapide que celle de l’hydrogène pendant la séquence principale, et les étoiles sont assez instables pendant ce stade. Les géantes rouges montent en luminosité bien au-delà de cette concentration d’étoiles.

Le « trou » des géantes jaunes

Dans la zone de température des étoiles de type F et G à des luminosités au-delà de 50 fois celle du soleil, il y a quasi-absence d’étoiles. Un tel « trou » peut s’expliquer par l’instabilité de telles étoiles : les étoiles de masses intermédiaires ou très massives, après la séquence principale, deviennent géantes rouges très rapidement (moins de 1 % de leur temps passé sur la séquence principale), tandis que les étoiles brûlant l’hélium en leur cœur sont instables dans cette région.

Les naines blanches

Anciens noyaux d’étoiles ayant éjecté leur enveloppe lors du stade de géante rouge, les naines blanches sont des étoiles très petites (de la taille de la Terre pour certaines) et très chaudes en surface. D’où cette position si particulière, en bas à gauche du diagramme de Hertzsprung-Russel. C’est le stade ultime des étoiles de masse inférieure à 8 masses solaires. Ces étoiles se refroidissent lentement pour devenir des naines noires, mais ce refroidissement prend plusieurs dizaines de milliards d’années, de sorte qu’aucune naine noire n’a été observée à ce jour. Contrairement aux autres étoiles, les naines blanches les plus lumineuses sont les moins massives, car le rayonnement d’une naine blanche diminue avec sa masse.

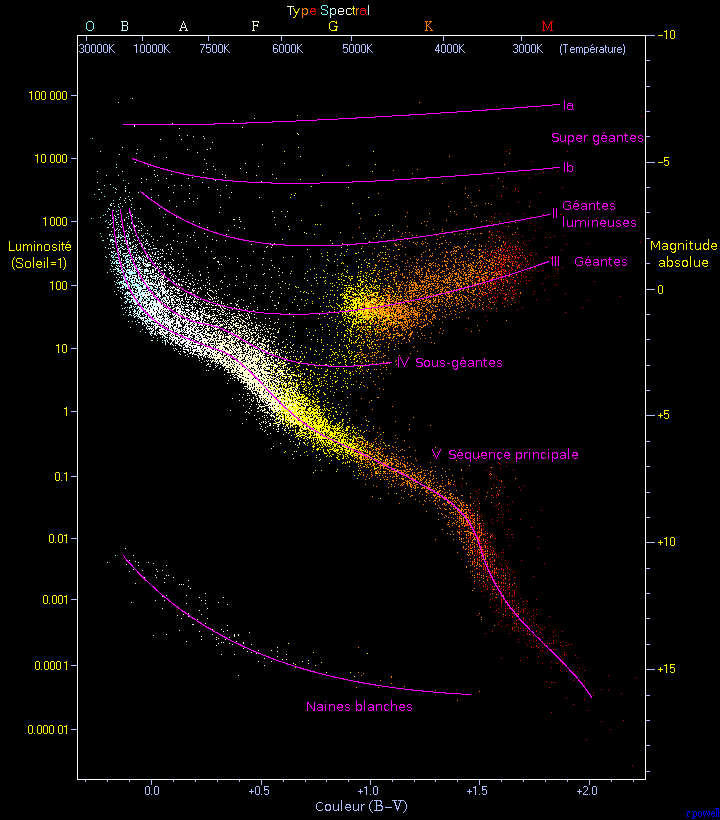
Autre présentation du diagramme de Hertzprung-Russell

–

25) Période synodique

La période synodique d’une planète est le temps mis par cette planète pour revenir à la même configuration Terre-planète-Soleil, c’est-à-dire à la même place dans le ciel par rapport au Soleil, vu de la Terre. Cette durée diffère de la période de révolution sidérale de la planète car la Terre elle-même se déplace autour du Soleil. En conséquence, il s’agit de la période de révolution apparente, la durée entre deux conjonctions planète-Soleil, telle qu’observée depuis la Terre. Le terme désigne de façon générale le temps séparant deux aspects identiques de l’objet (opposition, conjonction, quadrature, etc.) et dépend donc des trois corps impliqués. Les périodes synodiques des lunes de Mars, par exemple, dépendront des vitesses de révolution de Mars autour du Soleil et des lunes autour de Mars, ainsi que de la période de rotation de Mars sur elle-même.

Période synodique des planètes du Système solaire et de la Lune

Plus la planète est éloignée, moins elle parcourt son orbite au cours d’une année et plus sa période synodique se rapproche de la période sidérale de la Terre.

Périodes synodique et sidérales des planètes du système solaire
Planète	Période synodique (j)	Période sidérale (j)
Mercure	115,878	87,96935
Vénus	583,921361	224,7096
Mars	779,964	686,960
Jupiter	398,861	4 335,355
Saturne	378,094	10 757,737
Uranus	369,654	30 708,160
Neptune	367,486	60 224,904

En ce qui concerne la Lune, sa période de révolution vaut un « mois lunaire sidéral », soit 27,32 jours terrestres, et sa période synodique, autrement nommée « mois lunaire synodique », vaut 29,53 jours, la durée séparant deux phases identiques de la Lune consécutives (deux pleines lunes ou deux nouvelles lunes par exemple).

Correspondance entre période sidérale et période synodique

La relation entre les deux périodes a été calculée pour la première fois par Copernic dans le cas d’orbites circulaires.

On nomme T la période sidérale de la Terre, P la période sidérale de la planète et S sa période synodique.

Dans le cas d’une planète intérieure, plus proche du Soleil que la Terre, on trouve :

Dans le cas d’une planète extérieure, plus éloignée du Soleil que la Terre :

–

26) La “lumière cendrée”

Dans les jours qui précèdent ou suivent la Nouvelle Lune, alors qu’un fin croissant se dessine à l’horizon EST dans le ciel du matin (avant la Nouvelle Lune) ou à l’horizon OUEST dans le ciel du soir (après la Nouvelle Lune), on remarque que le reste du disque lunaire est légèrement éclairé. Il reçoit la lumière solaire renvoyée dans l’espace par la Terre.

En effet, en raison des nuages (essentiellement) et des océans (pour une très faible partie) qui ont un bon pouvoir réfléchissant, c’est environ 37 % de la lumière reçue par notre planète qui repart dans l’espace. Cette lumière cendrée suffit à éclairer faiblement notre satellite. Ce phénomène n’est observable qu’à cette période de la lunaison : le reste du temps, l’éclat lunaire est trop important pour déceler la lumière cendrée sur le reste du disque.

↑ Photo Olivier Sabbagh, GAP47 – Lune cendrée et Vénus – 19/08/2017 à 06h15

Il est tout à fait possible de photographier la lumière cendrée en utilisant un appareil photo numérique à condition de pouvoir débrayer les automatismes : on installe l’appareil sur un pied et on opte pour une mise au point à l’infini et des poses de 2 à 10 secondes.

La lumière cendrée, aussi connue aux États-Unis sous le joli nom de “Vieille Lune dans les bras de la Nouvelle Lune” apparaît sur cette photo qui a été prise à l’observatoire de Las Campanas dans le désert de l’Atacama au Chili le 18 janvier 2018. Une description de ce phénomène avec la lumière solaire reflétée par les océans et l’atmosphère de la Terre avait été consignée par écrit il y a 500 ans par Léonard de Vinci. Ce porquoi les américains l’appellent aussi le “Da Vinci Glow” (la lueur de Léonard de Vinci).

La magnifique inversion des couches atmosphériques apparait au-dessus de l’océan pacifique, éclairées par le Soleil couchant. ↓

–

27) Quasars

Un quasar (source de rayonnement astronomique quasi-stellaire, quasi-stellar astronomical radiosource), est une galaxie très énergétique avec un noyau galactique actif. Les quasars sont les entités les plus lumineuses de l’univers. Bien qu’il y ait d’abord eu une certaine controverse sur la nature de ces objets jusqu’au début des années 1980, il existe maintenant un consensus scientifique selon lequel un quasar est la région compacte entourant un trou noir supermassif au centre d’une galaxie massive. Leur taille est de 10 à 10.000 fois le rayon de Schwarzschild* du trou noir. Leur source d’énergie provient du disque d’accrétion entourant le trou noir.

Avec les télescopes optiques, la plupart des quasars ressemblent à de petits points lumineux, bien que certains soient vus comme étant les centres de galaxies actives (couramment connus sous l’abréviation AGN, pour Active Galaxy Nucleus). La majorité des quasars sont beaucoup trop éloignés pour être vus avec de petits télescopes, mais 3C 273, avec une magnitude apparente (ou relative) de 12,9 est une exception. À 2,44 milliards d’années-lumière, c’est un des objets lointains observables avec un équipement d’amateur. Certains quasars montrent de rapides changements de luminosité, ce qui implique qu’ils sont assez petits (un objet ne peut pas changer plus vite que le temps qu’il faut à la lumière pour voyager d’un bout à l’autre). Actuellement, le quasar ULAS J1120+0641 est le plus lointain jamais observé, et se situe à 12,9 milliards d’années-lumière de la Terre. On pense que les quasars gagnent en puissance par l’accrétion de matière autour des trous noirs supermassifs qui se trouvent dans le noyau de ces galaxies, faisant des « versions lumineuses » de ces objets connus comme étant des galaxies actives. Aucun autre mécanisme ne parait capable d’expliquer l’immense énergie libérée et leur rapide variabilité.

Vue d’artiste du quasar GB1508, entre le blazar (en blanc) et le disque (en jaune)

Structure

Un quasar est composé de trois grandes parties principales :

Le trou noir supermassif comportant la quasi-totalité de la masse du quasar (de quelques millions à quelques dizaines de milliards de fois la masse du Soleil). Il est également le centre du quasar.
Le disque d’accrétion est le disque formé par la matière qui tombe dans le trou noir. La force de friction engendrée par le frottement des gaz dans le disque génère une forte chaleur.
Les jets de gaz qui sont expulsés du disque d’accrétion par les lignes de champs magnétique du trou noir atteignent une vitesse proche de celle de la lumière.

NB : * En physique et en astronomie, le rayon de Schwarzschild est le rayon de l’horizon d’un trou noir de Schwarzschild, lequel est un trou noir dont la charge électrique et le moment cinétique sont nuls. Cela signifie qu’en dessous de ce rayon tous les photons (circulant à la vitesse de la lumière), ont (en oubliant qu’on est dans un cadre relativiste) des trajectoires elliptiques et ne peuvent s’échapper. Le demi-rayon de Schwarzschild ou rayon gravitationnel est la moitié d’un rayon de Schwarzschild (pour lequel ces trajectoires sont circulaires). Par extension, c’est une longueur intervenant dans la description relativiste du champ gravitationnel créé par une distribution de masse à symétrie sphérique. Il peut être défini, en première approximation, comme le rayon d’une sphère à partir de laquelle la masse de l’objet est tellement compacte que la vitesse de libération est égale à la vitesse de la lumière dans le vide, de sorte que la lumière elle-même ne peut s’en échapper. Il entre dans la définition du trou noir, modélisé par Karl Schwarzschild. En effet, si le rayon de la distribution de masse de l’objet considéré est inférieur au rayon de Schwarzschild, l’objet considéré est un trou noir dont l’horizon est la sphère de rayon égal au rayon de Schwarzschild.

Plus d’informations sur les quasars dans notre document pdf

–

28) Pulsars

Un pulsar est un objet astronomique produisant un signal périodique allant de l’ordre de la milliseconde à quelques dizaines de secondes. Ce serait une étoile à neutrons tournant très rapidement sur elle-même (période typique de l’ordre de la seconde, voire beaucoup moins pour les pulsars milliseconde) et émettant un fort rayonnement électromagnétique dans la direction de son axe magnétique.

Terminologie
Attesté dès 1969, le substantif masculin pulsar a été emprunté à l’anglais pulsar, un mot-valise de même sens, créé à partir de la locution pulsating star (proprement « étoile pulsante »), composée de pulsating (« vibrant ») et star (« étoile »). Ce mot vient de ce que, lors de leur découverte, ces objets ont dans un premier temps été interprétés comme étant des étoiles variables sujettes à des pulsations très rapides. Cette hypothèse s’est rapidement révélée incorrecte, mais le nom est resté. L’abréviation PSR est l’acronyme de l’anglais pulsating source of radio (emission), proprement « source pulsante d’ondes radio ».

Généralités
L’axe magnétique d’une étoile à neutrons n’étant en général, à l’instar de la Terre, pas parfaitement aligné avec son axe de rotation, la région d’émission correspond à un instant donné à un faisceau, qui balaie au cours du temps un cône du fait de la rotation de l’astre. Un pulsar se signale pour un observateur distant sous la forme d’un signal périodique, la période correspondant à la période de rotation de l’astre. Ce signal est extrêmement stable, car la rotation de l’astre l’est également, toutefois il ralentit très légèrement au cours du temps.

Les pulsars sont issus de l’explosion d’une étoile massive en fin de vie, phénomène appelé supernova (plus précisément supernova à effondrement de cœur, l’autre classe de supernovas, les supernovas thermonucléaires ne laissant pas derrière elles de résidu compact). Toutes les supernovas à effondrement de cœur ne donnent pas naissance à des pulsars, certaines laissant derrière elles un trou noir. Si une étoile à neutrons a une durée de vie virtuellement infinie, le phénomène d’émission caractéristique d’un pulsar ne se produit en général que pendant quelques millions d’années, après quoi il devient trop faible pour être détectable avec les technologies actuelles.

Les pulsars ont été découverts en 1967 de façon quelque peu fortuite par Jocelyn Bell (maintenant Jocelyn Bell-Burnell) et son directeur de thèse Antony Hewish qui étudiaient des phénomènes de scintillation réfractive dans le domaine radio et avaient de ce fait besoin d’un instrument mesurant des variations d’un signal radio sur des courtes durées (une fraction de seconde). L’instrument a de ce fait permis de détecter la variation périodique d’objets qui se sont avérés être des pulsars, le premier d’entre eux portant le nom de PSR B1919+21 (ou CP 1919 à l’époque). Cette découverte fut récompensée par le prix Nobel de physique, attribué en 1974 à Hewish ainsi que son collaborateur Martin Ryle, qui avaient construit l’instrument ayant permis la découverte, mais pas à Jocelyn Bell, chose qui apparaît aujourd’hui comme étant une injustice totale.

Le pulsar du Crabe (qui se nomme joliment PSR B0531+21) se situe dans le rémanent de la nébuleuse du Crabe (connue sous le nom de M1 ou SN 1054, dans la constellation du Taureau). À environ 6.200 années-lumière de nous, la nébuleuse et le pulsar sont issus de l’explosion d’une étoile géante en supernova, phénomène observé par les astronomes chinois en juillet 1054. Le pulsar a été découvert en 1968, il a une masse estimée à 1,4 fois le Soleil, pour un diamètre d’environ 20 km seulement ! Il effectue une rotation en 33 millisecondes, c’est-à-dire qu’il tourne sur lui-même 30 fois par seconde…

↑ Image composite visible/rayon X du pulsar du Crabe, né de la supernova historique SN 1054, montrant le gaz environnant la nébuleuse agité par le champ magnétique et le rayonnement du pulsar. Image NASA

↑ Le pulsar du Crabe est le pulsar le plus énergétique connu en termes de luminosité et en termes de période de rotation (environ 33 ms). La lente augmentation de sa période de rotation génère un rayonnement électromagnétique qui est plus de 100.000 fois plus intense que le Soleil, générant environ 4,5×10³¹ W. Ce rayonnement est entre autres responsable de la forte luminosité de la partie centrale de la nébuleuse du Crabe, générée par rayonnement synchrotron. (ici le son entendu est ce que l’on appelle sa “vibration électromagnétique”).

↑ Le son du pulsar du Crabe, capté dans une autre longueur d’onde

Les pulsars ont depuis permis le développement important de très nombreuses disciplines de l’astrophysique, allant de tests de la relativité générale et de la physique de la matière condensée, jusqu’à l’étude de la structure de la Voie lactée et bien sûr des supernovæ. L’étude d’un pulsar binaire, PSR B1913+16, a pour la première fois permis de mettre en évidence la réalité du rayonnement gravitationnel prédit par la relativité générale, et a également été récompensée du prix Nobel de physique (Russell Alan Hulse et Joseph Hooton Taylor, en 1993).

Du fait que l’émission d’un pulsar est cantonnée à un cône, un grand nombre de pulsars sont inobservables depuis la Terre, car celle-ci ne se trouve pas dans le cône balayé par le faisceau de nombreux pulsars. Néanmoins, plus de 2.000 pulsars sont connus à l’heure actuelle (2007), la quasi-totalité d’entre eux étant situés dans la Voie lactée ou certains de ses amas globulaires, les autres, très peu nombreux, étant situés dans les deux Nuages de Magellan. Même un pulsar aussi énergétique que le pulsar le plus énergétique connu (le pulsar du Crabe, aussi appelé PSR B0531+21) serait a priori indétectable s’il était observé depuis la galaxie d’Andromède (M31), aussi la Voie lactée et les Nuages de Magellan sont-elles les seules galaxies où il semble envisageable d’étudier ces objets avec les technologies actuelles.

Il existe une grande variété de types de pulsar (pulsars radio, pulsars X, pulsars X anormaux, magnétars, pulsars milliseconde), dont les propriétés dépendent essentiellement de leur âge et de leur environnement :

Les pulsars radio
Les pulsars X
Les pulsars gamma
Les pulsars X anormaux
Les magnétars
Les pulsars milliseconde

Plus d’informations sur les pulsars dans notre document pdf

–

29) Étoiles à neutrons

Une étoile à neutrons est un astre principalement composé de neutrons maintenus ensemble par les forces de gravitation. De tels objets sont le résidu compact issu de l’effondrement gravitationnel du cœur d’une étoile massive quand celle-ci a épuisé son combustible nucléaire. Cet effondrement s’accompagne d’une explosion des couches externes de l’étoile, qui sont complètement disloquées et rendues au milieu interstellaire, phénomène appelé supernova. Le résidu compact n’a d’étoile que le nom : il n’est plus le siège de réactions nucléaires et sa structure est radicalement différente de celle d’une étoile ordinaire. Sa masse volumique est en effet extraordinairement élevée, de l’ordre de mille milliards de tonnes par litre, et sa masse comprise dans une fourchette très étroite, entre 1,4 et 3,2 fois la masse du Soleil. Ainsi, une étoile à neutrons est une boule de seulement 20 à 40 kilomètres de diamètre.

À leur naissance, les étoiles à neutrons sont dotées d’une vitesse de rotation très élevée, de plusieurs dizaines de tours par seconde. Elles possèdent également un champ magnétique très intense, allant jusqu’à 10¹¹ teslas. Leur intérieur est également très atypique, étant principalement composé de neutrons dans un état superfluide. On y trouve également des proportions plus modestes de protons et d’électrons supraconducteurs. La région la plus centrale d’une étoile à neutrons est actuellement mal connue du fait de sa densité trop élevée. Elle peut être composée de neutrons ou de formes de matière plus exotiques.

Selon les circonstances, une étoile à neutrons peut se manifester sous divers aspects. Si elle tourne rapidement sur elle-même et qu’elle possède un puissant champ magnétique, elle projette alors le long de son axe magnétique un mince pinceau de radiations, et un observateur placé approximativement dans la direction de cet axe observera une émission pulsée par un effet de phare, appelée pour cette raison pulsar. Une étoile à neutrons située dans un système binaire peut arracher de la matière à son étoile compagnon et donner lieu à une émission pulsée ou continue dans le domaine des rayons X et gamma. Isolée et sans son émission pulsée, une étoile à neutrons est nettement plus difficile à détecter car seule l’émission thermique de sa surface est éventuellement décelable. Donc une étoile à neutrons peut devenir un pulsar, mais ce n’est pas toujours le cas !

Plus d’informations sur les étoiles à neutrons dans notre document pdf

–

30) Les trous noirs

En astrophysique, un trou noir est un objet céleste si compact que l’intensité de son champ gravitationnel empêche toute forme de matière ou de rayonnement de s’en échapper. De tels objets ne peuvent ni émettre, ni réfléchir la lumière et sont donc noirs, ce qui en astronomie revient à dire qu’ils sont invisibles. Toutefois, plusieurs techniques d’observation indirecte dans différentes longueurs d’ondes ont été mises au point et permettent d’étudier les phénomènes qu’ils induisent. En particulier, la matière happée par un trou noir est chauffée à des températures considérables avant d’être « engloutie » et émet une quantité importante de rayons X.

Envisagée dès le XVIII^e siècle, dans le cadre de la mécanique classique, leur existence, prédite par la relativité générale, est une certitude pour la quasi-totlité de la communauté scientifique concernée (astrophysiciens et physiciens théoriciens). Dans le cadre de la relativité générale, un trou noir est défini comme une singularité gravitationnelle occultée par un horizon absolu appelé horizon des événements. Selon la physique quantique, un trou noir est susceptible de s’évaporer par l’émission d’un rayonnement de corps noir appelé rayonnement de Hawking. Un trou noir ne doit pas être confondu avec un trou blanc ni avec un trou de ver.

Présentation et terminologie

Un trou noir possède une masse donnée, concentrée en un point que l’on appelle singularité gravitationnelle. Cette masse permet de définir une sphère appelée horizon du trou noir, centrée sur la singularité et dont le rayon est une limite maximale en deçà de laquelle le trou noir empêche tout rayonnement et a fortiori toute matière de s’échapper. Cette sphère représente en quelque sorte l’extension spatiale du trou noir. C’est ainsi que le terme « trou » est inapproprié : il serait plus correct de parler de « boule noire » pour conceptualiser concrètement sa forme physique réelle tridimensionnelle dans l’espace. Pour un trou noir de masse égale à celle du Soleil, son rayon vaut environ 3 kilomètres. À une distance interstellaire (en millions de kilomètres), un trou noir n’exerce pas plus d’attraction que n’importe quel autre corps de même masse; il ne s’agit donc pas d’un « aspirateur » irrésistible.

Par exemple, si le Soleil se trouvait remplacé par un trou noir de même masse, les orbites des corps tournant autour (planètes et autres) resteraient pour l’essentiel inchangées (seuls les passages à proximité de l’horizon induiraient un changement notable). Il existe plusieurs sortes de trous noirs. Lorsqu’ils se forment à la suite de l’effondrement gravitationnel d’une étoile massive, on parle de trou noir stellaire, dont la masse équivaut à quelques masses solaires. Ceux qui se trouvent au centre des galaxies possèdent une masse bien plus importante pouvant atteindre plusieurs milliards de fois celle du Soleil; on parle alors de trou noir supermassif (ou trou noir galactique). Entre ces deux échelles de masse, il existerait des trous noirs intermédiaires avec une masse de quelques milliers de masses solaires.

Des trous noirs de masse bien plus faible, formés au début de l’histoire de l’Univers, peu après le Big Bang, sont aussi envisagés et sont appelés trous noirs primordiaux. Leur existence n’est, à l’heure actuelle, pas confirmée. Il est par définition impossible d’observer directement un trou noir.

Il est cependant possible de déduire sa présence de son action gravitationnelle : soit par les effets sur les trajectoires des étoiles proches; soit au sein des microquasars et des noyaux actifs de galaxies, où de la matière, située à proximité, tombant sur le trou noir va se trouver considérablement chauffée et émettre un fort rayonnement X. Les observations permettent ainsi de déceler l’existence d’objets massifs et de très petite taille. Les seuls objets correspondant à ces observations et entrant dans le cadre de la relativité générale sont les trous noirs.

↓ Vidéo du journal “Le Monde” : Peut-on sortir d’un trou noir ?

http://www.dailymotion.com/video/x4ogey9

Pour en savoir plus sur les trous noirs, vous pouvez télécharger notre document pdf

–

31) Astéroïdes, astéroïdes géocroiseurs, astéroïdes troyens, centaures

Il existe, dans le système solaire, un nombre quasiment incalculable de “petits corps”. Ce sont principalement des astéroïdes (de plusieurs sortes), des comètes et des petits corps indéterminés situés à des endroits différents du système solaire.

A – Les astéroïdes “classiques”

Un astéroïde est une planète mineure (voir ci-dessous le diagramme d’Euler des corps du système solaire) qui est composée de roches, de métaux et de glaces, et dont les dimensions varient de l’ordre du mètre (limite actuelle de détection) à plusieurs centaines de kilomètres.

Lorsque leur diamètre avoisine ou dépasse 1.000 km, ce qui est rarissime, leur forme peut être sphérique et ils peuvent prendre alors également le statut de planète naine. C’est le cas de Cérès. Dans le cas contraire, ils ont généralement une forme irrégulière et font partie de la classe des petits corps.
Les astéroïdes (appelés météoroïdes pour les plus petits) pénétrant dans l’atmosphère d’un autre corps créent des météores. Si une partie de l’astéroïde réussit à toucher la surface du corps impacté, elle forme alors une météorite et peut créer un cratère d’impact.

En 1801, le premier astéroïde est découvert et nommé Cérès; il est le plus grand du système solaire. Depuis, plus de 580 000 astéroïdes du Système solaire ont été répertoriés (en 2015, date à laquelle une sonde spatiale a tourné pour la première fois autour de Cérès). Les premiers astéroïdes découverts ont une orbite située entre celles de Mars et de Jupiter, aussi cette zone est-elle appelée la ceinture principale d’astéroïdes. Une autre zone située au-delà de l’orbite de Neptune comporte une forte concentration d’astéroïdes : la ceinture de Kuiper.

La composition des astéroïdes de la ceinture de Kuiper est plus riche en glace et plus pauvre en métaux et en roches, ce qui les apparente plus à des noyaux cométaires. Contrairement aux comètes les astéroïdes sont généralement inactifs, cependant quelques-uns ont été observés avec une activité cométaire (développement d’une queue à l’approche du Soleil).

On suppose que les astéroïdes de la ceinture principale sont des restes d’un disque protoplanétaire qui ne se sont pas regroupés, notamment à cause de l’influence gravitationnelle de Jupiter, qui n’aurait pas permis l’accrétion d’une planète au niveau actuel de la ceinture principale.

Certains astéroïdes ont des satellites. Les spécialistes estiment que 16 % des astéroïdes pourraient être accompagnés d’un satellite (ou plusieurs). En 2015 on avait dénombré 225 satellites d’astéroïdes. Le premier à avoir été découvert en 1993 est Dactyle, satellite de l’astéroïde Ida. Voir ci-dessous ↓

L’astéroïde Sylvia (260 km de long) est doté de deux petits satellites de 18 et 7 km, Romulus et Rémus.

L’astéroïde Eros a été approché par la sonde Near, qui a survolé l’objet en 2000 (photo et vidéo ci-dessous). La sonde s’est ensuite posée sur l’astéroïde ↓

Couleur des astéroïdes :

La composition des astéroïdes est évaluée d’après leur spectre optique mesurant la lumière réfléchie, qui correspond à la composition de leur surface. Celle des météorites est connue avec l’analyse des fragments retrouvés sur Terre. Le système classique de classification spectrale des astéroïdes, élaboré en 1975, les classe selon un système basé sur leur couleur, leur albédo et leur spectre optique. Ces propriétés étaient censées correspondre à la composition de leur surface. Il faut noter, cependant, que certains types sont plus facilement détectables que d’autres. Ainsi, ce n’est pas parce que la proportion d’astéroïdes d’un type donné est plus importante qu’ils sont effectivement plus nombreux. Il existe des systèmes de classification plus récents, dont deux se démarquent : Tholen et SMASS.

À l’origine, la classification des astéroïdes se basait sur des suppositions au sujet de leur composition :

type C – carbone
type S – silice
type M – métallique

Ceci a porté à confusion, car le type spectral d’un astéroïde ne garantit pas sa composition.

B – Les astéroïdes “géocroiseurs”

En astronomie, les astéroïdes géocroiseurs sont des astéroïdes évoluant à proximité de la Terre. Pour les nommer on utilise souvent l’abréviation ECA (de l’anglais Earth-Crossing Asteroids, astéroïdes croisant l’orbite de la Terre), astéroïdes dont l’orbite autour du Soleil croise celle de la Terre, ayant une distance aphélique inférieure à celle de Mars, soit 1,381 UA (valeur d’1,300 UA fixée par les spécialistes américains).

Les NEA (Near-Earth Asteroids, astéroïdes proches de la Terre) sont aussi souvent, par abus et à tort, appelés en français géocroiseurs même si certains ne croisent pas l’orbite de la Terre (voir ci-dessous). Le terme francophone de circastéroïde a également été utilisé par certains auteurs pour cette même définition.

Parmi les NEA, on distingue trois familles principales :

les Atons, qui possèdent un demi-grand axe de moins d’une UA;
les Apollons, qui croisent l’orbite de la Terre avec une période supérieure à un an;
les Amors, qui sont des frôleurs extérieurs et ne sont donc pas des géocroiseurs au sens strict du terme.

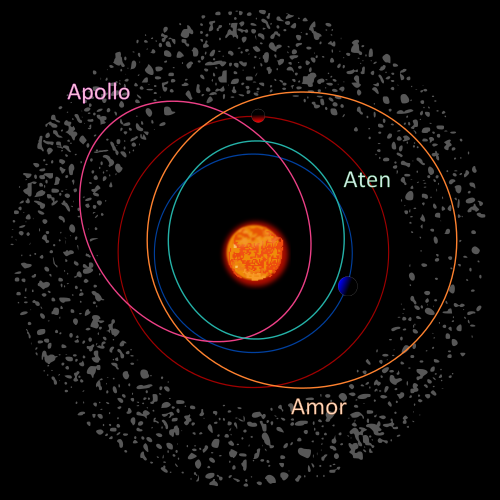
↑ Classification des astéroïdes géocroiseurs (en bleu l’orbite de la Terre)

Au 31 décembre 2017, la NASA a identifié :

106 comètes de type géocroiseur
18 astéroïdes géocroiseurs de type Atira
1.284 astéroïdes géocroiseurs de type Aten
9.520 astéroïdes géocroiseurs de type Apollo
6.618 astéroïdes géocroiseurs de type Amor

soit un total de 17.440 astéroïdes géocroiseurs. Parmi eux 886 ont un diamètre d’au moins un kilomètre, et 7.991 un diamètre supérieur ou égal à 140 mètres. La NASA considère que le recensement des premiers est terminé, et se fixe désormais comme objectif de répertorier 90% des seconds.

On appelle astéroïdes géofrôleurs (en abrégé EGA, sigle de Earth-Grazing Asteroids) les astéroïdes ayant une distance minimale à l’orbite terrestre inférieure à 0,100 UA et PHA (sigle de Potentially Hazardous Asteroids, astéroïdes potentiellement dangereux APD en français) ceux de magnitude absolue H < 22 (soit plus de 130 mètres de diamètre moyen) et qui peuvent passer à l’intérieur d’un cercle de 0,05 UA situé dans le plan de l’écliptique à 1,0 UA du Soleil.

Les astéroïdes géocroiseurs appartiennent au groupe des objets géocroiseurs (en anglais, NEO : Near Earth Object), qui comprend également quelques comètes. Certains de ces objets étant susceptibles de heurter la Terre, ils font l’objet d’une recherche et d’un suivi particulier.

Détection des astéroïdes géocroiseurs

Dans la seconde moitié du XX° siècle, différents travaux scientifiques ont permis de découvrir la menace que constituerait l’impact d’astéroïdes pour la vie sur Terre. La NASA a mis sur pied en 1998 le programme Spaceguard de détection des astéroïdes géocroiseurs (dont l’orbite coupe celle de la Terre) ayant un diamètre supérieur à 1 km. Cette dimension a été retenue car l’impact d’un tel astéroïde pourrait amener l’extinction de l’humanité. On estime qu’il existe moins de 1.200 astéroïdes dans cette catégorie. Un objet de ce type frappe la Terre environ tous les 500 000 ans. Fin 2008, près de 90 % des objets de cette dimension ont été recensés. Ces dernières années plusieurs programmes de détection de la NASA (LINEAR, NEAT, Spacewatch, LONEOS, Catalina Sky Survey, ADAS) ou d’autres pays (CINEOS,…) ont été mis sur pied pour identifier les objets de plus petite taille. Ces programmes utilisent des télescopes dédiés à cette tâche et basés sur Terre. Le programme NEOWISE exploite les capacités du télescope spatial infrarouge WISE pour identifier une sous-catégorie des astéroïdes géocroiseurs baptisée PHA (Potentially hazardous asteroid) qui se définit comme ceux dont l’orbite coupe celle de la Terre à moins de 8 millions de km de celle-ci (soit 20 fois la distance Terre-Lune). Les résultats de cette étude, achevée en 2012, permettent d’estimer qu’il existe environ 4.000 à 5.000 astéroïdes de ce type ayant une taille comprise entre 100 mètres et un kilomètre dont 20 à 30 % sont aujourd’hui identifiés. Il existe par ailleurs un demi million d’astéroïdes géocroiseurs d’une taille comprise entre 50 et 100 mètres. Un de ces objets frappe la Terre statistiquement tous les mille ans (un astéroïde de moins de 50 mètres tous les 100 ans). Début 2013 seule une faible fraction de ces objets a été détectée.

↑ Image quelque peu anxiogène des orbites des astéroïdes géocroiseurs de plus de 140 mètres suivis en 2013

Risques d’impacts et conséquences selon la taille des astéroïdes :

Taille du corps : < 10 m :
- Fréquence d’impact : 200 fois par an ;
- Conséquence d’une chute sur la Terre : aucune => désintégration dans l’atmosphère.

Taille du corps : 10 à 100 m :
- Fréquence d’impact : une fois par siècle (exemples connus : Meteor Crater, Arizona, il y a 50 000 ans ; Toungouska, Sibérie, 30 juin 1908) ;
- Conséquence possible d’une chute sur la Terre : destruction d’une ville, raz-de-marée.

Taille du corps : 100 m à 1 km :
- Fréquence d’impact : une fois tous les 5 000 à 30 000 ans
- Conséquence probable d’une chute sur la Terre : environ cinq millions à cent millions de morts.

Taille du corps : > 5 km :
- Fréquence d’impact : une fois tous les 100 millions d’années ;
- Conséquence d’une chute sur la Terre : hiver d’impact, disparition de l’humanité, catastrophe globale.

Taille du corps : de 100 à 200 km
- Fréquence d’impact : une fois tous les 1 milliard d’années ;
- Conséquence d’une chute sur la Terre : vaporisation des océans, disparition de toute forme de vie sur Terre.

Outre les géocroiseurs, il existe d’autres regroupements d’astéroïdes, suivant qu’ils croisent l’orbite d’une autre planète du Système solaire. Certains astéroïdes peuvent faire partie de plusieurs regroupements. Il est à noter que si le terme de géocroiseur est répandu (géo- étant le préfixe associé à la Terre), ceux qui suivent sont très rarement employés.

Herméocroiseurs : croisent l’orbite de Mercure
Cythérocroiseurs : croisent l’orbite de Vénus
Géocroiseurs : croisent l’orbite de la Terre
Aréocroiseurs : croisent l’orbite de Mars
Zénocroiseurs : croisent l’orbite de Jupiter
Kronocroiseurs : croisent l’orbite de Saturne
Ouranocroiseurs : croisent l’orbite d’Uranus
Poséidocroiseurs : croisent l’orbite de Neptune
Hadéocroiseurs : croisent l’orbite de Pluton (qui n’est plus reconnue comme planète depuis 2006 mais comme une planète naine).

C – Les astéroïdes “troyens”

Ce sont des astéroïdes qui ne présentent, à priori, aucun danger pour la Terre, dans la mesure où ils partagent l’orbite d’une planète, dans un équilibre très stable puisqu’ils sont situés aux points de Lagrange 4 et 5 de l’orbite de leur planète. Voir, dans ce glossaire à «Lagrange, Points de Lagrange».

Il y en a plus de 6.300 recensés actuellement dans le système solaire, dont plus de 99% sont situés sur l’orbite de Jupiter autour du Soleil.

dans le système Soleil-Jupiter, on recense (en 2011) environ 6.300 astéroïdes aux points L₄ et L₅
dans le système Soleil-Neptune, huit
dans le système Soleil-Mars, quatre
dans le système Saturne-Téthys, les points L₄ et L₅ sont occupés par Télesto et Calypso, respectivement
dans le système Saturne-Dioné, Hélène et Pollux occupent ces points

Curieusement, il semblerait que le système Soleil-Saturne ne soit pas en mesure d’accumuler des troyens du fait des perturbations joviennes.

D – Les “centaures”

En astronomie, les centaures sont des petits corps glacés qui gravitent autour du Soleil entre Jupiter et Neptune. Ils ont été nommés d’après la race mythique des centaures. Les centaures sont généralement de petite taille, et le membre le plus grand, (10199) Chariclo, a un diamètre de seulement 302 km.

Les centaures, du fait de leurs orbites très instables (car influencées par les planètes géantes gazeuses) et du fait de la taille de certains d’entre-eux, peuvent présenter de réels dangers pour la Terre en cas de collision avec notre planète.

Certains centaures ont une nature incertaine et/ou double. On a en effet constaté qu’il y en avait qui se comportaient parfois comme des comètes en présentant une queue à l’approche du Soleil. En conséquence, il y a des centaures qui sont catalogués comme étant de nature double astéroïde/comète.

On a découvert que deux des plus gros centaures (au moins), Chariclo et Chiron étaient dotés d’un ou deux anneaux. Chariclo, le plus grand centaure connu a deux anneaux de respectivement 7 et 3 km de largeur. Ces anneaux pourraient être stabilisés (comme sur Saturne) par de minuscules satellites invisibles pour le moment. Chiron serait, lui aussi, doté de deux anneaux (à confirmer). Ces anneaux n’ont pu être décelés que grâce à l’occultation d’une étoile par ces anneaux.

Définition
Un centaure peut être défini, en première approximation, comme un astéroïde qui orbite entre Jupiter et Neptune et croise l’orbite d’une ou plusieurs planètes géantes gazeuses. Plus précisément :

pour le Centre des planètes mineures, un centaure est un objet dont le périhélie est au-delà de l’orbite de Jupiter et dont le demi-grand axe est à l’intérieur de l’orbite de Neptune;
pour le Committee for Small-Body Nomenclature, un centaure est un planétoïde transjovien qui croise ou s’approche d’une planète géante gazeuse mais dont l’orbite est instable, n’étant en résonance de moyen mouvement 1:1 avec aucune planète majeure;
pour la JPL Small-Body Database, de façon similaire, un centaure est un objet dont le demi-grand axe est supérieur à 5,5 ua et inférieur à 30,1 ua;
pour le Deep Ecliptic Survey, un centaure est un objet non résonant dont le périhélie de son orbite osculatrice reste inférieur au demi-grand axe de l’orbite osculatrice de Neptune.

Histoire
Le premier centaure fut découvert en 1920, il s’agissait de Hidalgo mais on ne connaissait pas encore l’origine de ce corps. Le premier centaure identifié fut Chiron en 1977, que l’on crut d’abord être un satellite de Saturne. En approchant de son périhélie, il développa une queue cométaire et fut reclassé comme comète (sous le nom de 95P/Chiron). Il est désormais considéré à la fois comme un astéroïde et une comète, quoique d’une taille nettement plus grande que les comètes classiques. On pense généralement que la plupart des centaures sont des astéroïdes qui ont été éjectés de la ceinture de Kuiper pour venir s’installer dans le système solaire interne.

Exploration
Aucun centaure n’a, à l’heure actuelle (2014), été photographié de près par une sonde spatiale, bien qu’il semble que Phœbé, l’un des satellites de Saturne, photographié par la sonde Cassini en 2004, soit un centaure capturé. Le télescope Hubble a également glané quelques informations sur la surface de (8405) Asbolos. En 2010, la sonde New Horizons devait survoler de loin un autre centaure, (83982) Crantor, mais les images furent décevantes.

Orbites
Les centaures ne sont pas situés sur des orbites stables à l’échelle de la centaine de milliers d’années. Des études de leurs orbites semblent indiquer qu’il s’agit d’un état orbital de transition entre la ceinture de Kuiper et les comètes à courte période. Il est possible qu’il s’agisse d’objets de la ceinture de Kuiper perturbés gravitationnellement et dont l’orbite a croisé celle de Neptune. L’orbite des centaures est chaotique et évolue rapidement lorsque l’objet s’approche de l’une des planètes géantes du Système solaire. Certains centaures finissent par croiser l’orbite de Jupiter. S’ils démontrent une activité cométaire, ils sont reclassifiés comme comètes. À terme, il semble que leur destin doive se conclure par une collision avec le Soleil (ou une planète) ou bien par une éjection du Système solaire.

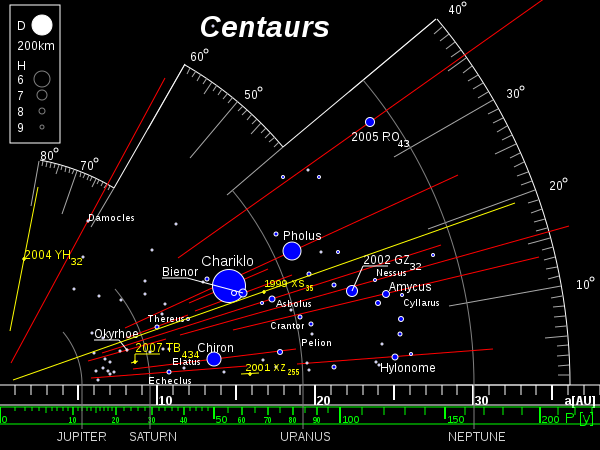
Le diagramme ci-dessus ↑ illustre les orbites des centaures connus par rapport aux orbites des planètes. Pour quelques objets, l’excentricité des orbites est représentée par les segments rouges (du périhélie à l’aphélie) avec l’inclinaison représentée sur l’axe vertical.

Pour illustrer la fourchette des paramètres des orbites, quatre objets avec les orbites extrêmes ont été montrés en (jaune) :

2005 VB₁₂₃, sur l’orbite la plus inclinée (~39°) mais aussi presque circulaire (la plus petite excentricité : < 0.01);
(8405) Asbolos, sur l’orbite la plus excentrique (excentricité = 0,69);
2001 XZ₂₅₅, sur une orbite presque coplanaire avec l’écliptique (inclinaison < 3°).

Les histogrammes présentent la distribution de l’inclinaison i (intervalle 5°) et de l’excentricité e (intervalle 0,05) des orbites.

Couleur des centaures
Les centaures présentent une extraordinaire diversité de couleurs défiant toute tentative de modéliser de façon simple leur composition.

L’indice de couleur est la mesure des différences de magnitude apparente de l’objet vu à travers des filtres bleu (B), neutre (V) vert-jaune et (R) rouge.

Les centaures peuvent être regroupés en deux classes :

Très rouges, comme Pholos
Bleu (bleu gris ou neutre selon les auteurs) comme Chiron

Les nombreuses théories qui tentent d’expliquer ces différences de couleur peuvent à leur tour être classifiées en deux catégories :

celles qui expliquent la différence de couleur comme une conséquence de la « vraie » différence de composition et d’origine,
celles qui traitent la différence de couleurs juste comme un simple résultat de modifications par la radiation et l’activité typique aux comètes.

Comme exemple de la deuxième catégorie, la couleur rougeâtre de Pholos serait due à une croûte de matière organique irradiée alors que Chiron aurait eu sa couche de glace exposée comme résultat de ses épisodes de comète. Selon une autre explication, Pholos aurait été expulsé très récemment de la ceinture de Kuiper et la modification de la surface n’a pas encore eu lieu. Une autre théorie suggère plusieurs processus en compétition, la radiation rendant l’objet plus rouge et les collisions avec l’activité de comète le rendant plus bleu.

–

32) Analemme

L’analemme est une figure obtenue en juxtaposant les positions du Soleil dans le ciel chaque jour (ou à intervalles réguliers) à la même heure et durant une année. On l’obtient donc à l’aide d’un appareil photo ou sur un ordinateur avec un logiciel. Depuis la Terre, l’analemme a la forme d’un 8 étiré et dissymétrique, avec une boucle beaucoup plus petite que l’autre. Cette forme est plus ou moins inclinée par rapport à l’horizontale selon l’heure choisie (elle est verticale si on note la position du Soleil à midi [heure solaire]). La largeur de la forme indique la variation de la durée du jour, due au fait que la vitesse de la Terre varie (plus grande à la périhélie, plus faible à l’aphélie), en raison de la forme elliptique de son orbite. (Futura Sciences)

Cette image montre un analemme pris tous les quelques jours près du village de Callanish dans les îles des Hébrides extérieures, sur l’île Lewis, en Écosse, près des Pierres de Callanish, un cercle de pierres construit vers 2.700 av. J.C. pendant l’Âge du Bronze. On ne sait pas si la configuration de ces pierres a, ou non, une signification astronomique. Lors des solstices (été, hiver) le Soleil se situe en haut ou en bas de l’analemme. Lors des équinoxes la position du Soleil se trouve aux points médians mais pas aux points d’intersection.

–

33) Le mouvement rétrograde des planètes

Cette vue composite d’images espacées de 5 à 9 jours, du 20 avril (en bas à droite) jusqu’au 5 novembre 2018 (en haut à gauche) montre le mouvement rétrograde de la planète Mars vu dans le ciel de la Terre. Mais Mars ne recule pas à cause de la direction de son orbite. En fait, le mouvement apparent de la planète par rapport aux étoiles situées en arrière-plan est due au mouvement de la Terre, elle-même sur sa propre orbite. Le mouvement rétrograde peut être constaté à chaque fois que la Terre rattrape et dépasse les planètes ou objets qui orbitent plus loin du Soleil (Mars, les gros astéroïdes de la ceinture, Jupiter, Saturne, Uranus, Neptune voire Pluton et au-delà) car la Terre tourne plus rapidement sur son orbite. Cela se produit également (mais différemment) pour les planètes “internes” (entre le Soleil et la Terre : Mercure et Vénus). Voir les deux animations ci-dessous :

↑ Explication graphique du mouvement rétrograde des planètes “externes”

↑ Explication graphique du mouvement rétrograde des planètes “internes”

↓ Autre explication graphique

↑ Le dessin ci-dessus schématise l’observation du mouvement d’une planète extérieure par projection sur la sphère des étoiles fixes. La Terre et la planète extérieure sont supposées évoluer sur des cercles (en réalité des ellipses de faible excentricité) dont le centre est le Soleil. La Terre (en bleu) se déplace deux fois plus vite (en vitesse angulaire) que la planète observée (en rouge). La Terre prend successivement les positions numérotées 1, 2, …, 5 sur sa trajectoire. Les observations de la planète sont schématisées par des demi-droites partant depuis la Terre et passant par la planète. Les mouvements apparents de cette dernière se lisent par projection sur la sphère des étoiles fixes (considérablement rapprochée sur le schéma), c’est-à-dire grâce aux points rouges numérotés 1, 2, …, 5 sur le schéma plan. Étonnamment, la planète semble alors reculer entre les positions 2, 3 et 4.

Dans la vision géocentrique d’Aristote et Ptolémée, il avait fallu “inventer” un système complexe basé sur des épicycles pour essayer de coller à la réalité observée de ces phénomènes rétrogrades. Voir, dans ce même glossaire, le point n° 9 (Géocentrisme et Héliocentrisme).

–

34) Classification des étoiles selon leur couleur (et donc leur température)

Pour mémoriser l’ordre des types spectraux (OBAFGKM), les anglophones utilisent la phrase « Oh, Be A Fine Girl/Guy, Kiss Me! », ce qui se traduit par « Oh! Sois une gentille fille/un gentil gars, embrasse-moi ». La raison de l’arrangement étrange des lettres est historique. Quand les premiers spectres d’étoiles furent pris, on remarqua que la raie de l’hydrogène variait beaucoup et l’on classa les étoiles selon l’intensité de la raie de Balmer : de A, la plus forte, à Q, la plus faible. Puis les raies d’autres éléments chimiques vinrent en jeu : les raies H et K du calcium, la raie D du sodium, etc. Plus tard, il apparut que beaucoup de ces classes se chevauchaient et furent retirées. Ce n’est que bien plus tard encore qu’on découvrit que l’intensité des raies dépendait essentiellement de la température de surface de l’étoile. Actuellement, ces classes sont subdivisées à l’aide des chiffres (0-9) : A0 pour les étoiles les plus chaudes de la classe A et A9 pour les moins chaudes. Par exemple, le soleil est une étoile de type G2.

Plus récemment, la classification a été étendue en W O B A F G K M L T Y et R N C S, où W sont les étoiles Wolf-Rayet, L, T et Y représentent des étoiles extrêmement froides, des naines brunes, et R N C S sont utilisés pour les étoiles carbonées.

N’oublions pas que l’étude de l’évolution des étoiles, quant à leur couleur et à leur température, ne peut pas se faire sans se référer, en parallèle, au fameux diagramme de Hertzsprung-Russell que vous pouvez voir en détail dans cette même page de notre glossaire astronomique à : Diagramme H-R

La classification spectrale des étoiles

1) Type O

Les étoiles de type O sont très chaudes (température de surface : 35 000 K pour delta Orionis) et très lumineuses et de couleur bleue. Par exemple, Naos, dans la constellation de la Poupe, brille près d’un million de fois plus fort que le Soleil. Ces étoiles possèdent des raies d’hélium intenses et des raies d’hydrogène assez faibles, elles émettent principalement dans l’ultraviolet. Ces étoiles sont si énergétiques qu’elles développent un fort vent stellaire et donc perdent de la matière qui forme alors des enveloppes donnant des raies en émission (type Oe pour les émissions dans l’hydrogène, type Of pour les émissions dans l’hélium II et l’azote III).

Spectre d’une étoile de type O5v

Une géante bleue est une étoile très chaude, très brillante et très massive (plus de 18 masses solaires), de couleur bleue et de type spectral O ou B. Dans le diagramme de Hertzsprung-Russell, les géantes bleues se trouvent dans le coin supérieur gauche à cause de leur luminosité et de leur couleur. Ce sont, généralement des étoiles de la séquence principale qui brûlent leur hydrogène. Cependant leur masse est suffisante pour leur permettre d’entamer la combustion de l’hélium une fois celle de l’hydrogène achevée. Très rapidement, l’étoile passera à la combustion du carbone, puis à celle de l’oxygène. Elle aura alors constitué un noyau de fer, élément trop stable pour que sa combustion soit possible, quelle que soit la masse de l’étoile. L’équilibre maintenu dans l’étoile par les réactions thermonucléaires étant subitement rompu, elle explosera en une gigantesque supernova. Les géantes bleues sont extrêmement lumineuses, de magnitude absolue -5, -6 ou même moins. Leur température de 20 000 K ou plus est suffisamment élevée pour qu’une partie non négligeable de l’énergie qu’elles émettent soit dans le domaine de l’ultraviolet, donc invisible à nos yeux. La majorité des étoiles de ce type se trouvent dans les associations O-B, des grands groupes d’étoiles jeunes. Du fait de leur masse élevée, leur durée de vie est très courte, de l’ordre de 10 à 100 millions d’années. Les théories actuelles prédisent que la plupart d’entre elles finiront en supernova. Certaines des étoiles les plus brillantes visibles dans le ciel sont des géantes bleues; par exemple Beta Orionis (Rigel) et Alpha Cygni (Deneb), mais dans l’ensemble, à cause de leur courte durée de vie, les géantes bleues sont assez rares.

2) Type B

Les étoiles de type B sont aussi très lumineuses et chaudes (température de surface : 13 000 K); Rigel, dans la constellation d’Orion, est une supergéante bleue de classe B. Leur spectre possède des raies d’hélium neutre et les raies d’hydrogène sont assez faibles (elles sont appelées raies de Balmer). Les étoiles de type O et B sont si puissantes qu’elles ne vivent que fort peu de temps. Elles ne s’écartent donc que peu de l’endroit où elles se sont formées. Ainsi, elles ont tendance à s’assembler en ce qu’on appelle des associations OB1 qui regroupent ces étoiles au sein d’un immense nuage moléculaire. L’association OB1 d’Orion forme un bras entier de la Voie lactée et contient toute la constellation d’Orion. C’est la présence d’étoiles très brillantes et non leur nombre qui fait que les bras des galaxies paraissent plus brillants. On peut rajouter que parmi les cent étoiles les plus brillantes, un tiers sont des étoiles de type B. Certaines étoiles B montrent des raies en émission dans leur spectre. Selon que les raies soient des raies interdites ou des raies normales, on parle d’étoiles « B[e] » ou « Be » (le « e » pour émission).

Spectre d’une étoile de type B2ii

3) Type A

Les étoiles de type A (appelées étoiles blanches de la séquence principale) sont parmi les plus communes visibles à l’œil nu. Deneb, dans la constellation du Cygne, et Sirius, l’étoile la plus brillante du ciel dans le visible, sont deux étoiles de classe A. Comme toutes celles de ce type, elles sont blanches, leur spectre possède des raies d’hydrogène assez intenses (raies de Balmer) et montre plus faiblement la présence de métaux ionisés (raie K du calcium ionisé). Certaines d’entre elles présentent des caractéristiques remarquables notées Am ou Ap. Elles font partie des étoiles à fort champ magnétique (taches) ou présentant de fortes concentrations de certains métaux (par lévitation due aux forces radiatives) renforçant les raies spectrales de ces éléments chimiques.

Spectre d’une étoile de type A2i

4) Type F

Les étoiles de classe F sont encore très lumineuses (température de surface : 7 200 K à 6 000 K), et sont en général des étoiles de la séquence principale, comme upsilon Andromedae A dans la constellation d’Andromède, Canopus, l’Étoile polaire, ou encore Procyon A. Leur spectre est caractérisé par des raies d’hydrogène plus faibles que dans les étoiles A et la présence de raies des métaux neutres et ionisés (Fe I, Fe II, Ti II, Ca I, Ca II, Mg I, etc.).

Spectre d’une étoile de type F2iii

En astronomie, la séquence principale est une bande continue et bien distincte d’étoiles qui apparaissent sur des diagrammes où l’abscisse est l’indice de couleur B-V et l’ordonnée la luminosité ou, en sens inverse, la magnitude absolue des étoiles. Ces diagrammes couleur/luminosité sont connus sous le nom de diagramme de Hertzsprung-Russell, d’après leurs co-inventeurs Ejnar Hertzsprung et Henry Norris Russell. Les étoiles figurant dans cette bande sont connues sous le nom d’étoiles de la série principale, ou « étoiles naines ». Ainsi, environ 90 % des étoiles observées au-dessus de 0,5 M_☉ sont sur la séquence principale. La séquence principale désigne aussi le stade principal de l’évolution d’une étoile : c’est pendant cette période que ses caractéristiques correspondent à celles de la séquence principale du diagramme HR et qu’elle s’y trouve effectivement représentée.

5) Type G

Les étoiles de classe G (ou naine jaune) sont les mieux connues, pour la seule raison que le Soleil appartient à cette classe. Elles possèdent des raies d’hydrogène encore plus faibles que celles de classe F et des raies de métaux ionisés ou neutres. Les raies du Ca II H et K sont très prononcées. La classe G est l’une des dernières (outre K et M, ci-dessous) où l’on distingue (étant donné la température de surface de 5 000 à 6 000 K) des raies moléculaires encore assez fortes (CH, CN, C₂, OH). Elles doivent d’ailleurs leur nom « G » à la molécule CH qui présente une forte absorption vers 430 nm identifiée par Fraunhofer par la lettre G. Alpha Centauri A est une étoile de classe G.

Spectre d’une étoile de type G5iii

Une étoile jaune de la séquence principale, appelée communément naine jaune, est une étoile de type G V (lire « G cinq »), c’est-à-dire une étoile appartenant à la séquence principale (classe de luminosité V) de type spectral G (étoile jaune). Sa masse est comprise entre 0,8 et 1,2 masse solaire. Ce type d’étoile représente environ 10 % des étoiles de la Voie lactée et le Soleil en est un exemple typique.

Caractéristiques

Les naines jaunes transforment dans leur cœur de l’hydrogène en hélium, par un processus de fusion nucléaire. Le mot « naine » utilisé pour désigner ces étoiles fait référence à leur classe de luminosité V. Leur température de surface est comprise entre 5 000 et 6 000 °C environ, et leur couleur jaune vif, presque blanc. La durée de vie d’une telle étoile est d’environ 10 milliards d’années. À la fin de leur vie, ces étoiles se mettent à grossir démesurément, pour devenir des géantes rouges (comme c’est le cas de Alpha Tauri par exemple). Lorsque ceci arrivera au Soleil, il s’étendra jusqu’à engloutir entièrement Mercure, Vénus et la Terre. Plus tard il s’effondrera à nouveau sur lui-même, laissant derrière lui une bonne partie des gaz le composant, pour former une naine blanche entourée d’une nébuleuse planétaire.

Naines jaunes remarquables

Le Soleil (à gauche) comparé à Tau Ceti (à droite)

Le Soleil est l’exemple le plus connu de naine jaune. Kepler-22 abrite Kepler-22b, la première exoplanète découverte orbitant dans la zone habitable de son étoile. Environ 10 % des étoiles de la Voie lactée sont des naines jaunes. Parmi les plus notables d’entre elles, on peut citer Alpha Centauri A, Tau Ceti, et 51 Pegasi.

6) Type K

Les étoiles de classe K (ou naine orange) sont des étoiles de couleur orange, légèrement moins chaudes que le Soleil (température de surface : 4 000 K). Certaines, comme Antarès, sont des géantes rouges alors que d’autres, telle que alpha Centauri B, sont des étoiles de la séquence principale. Elles possèdent des raies d’hydrogène très faibles, voire inexistantes, et surtout des raies de métaux neutres. Quelques composés moléculaires y sont visibles : CH, CN, monoxyde de carbone CO, ainsi que les larges bandes de monoxyde de titane TiO pour les plus froides.

Spectre d’une étoile de type K4iii

En astronomie, une étoile orange de la séquence principale, appelée communément naine orange, est une étoile de type K V (lire « K cinq »), c’est-à-dire une étoile appartenant à la séquence principale (classe de luminosité V) de type spectral K (étoile orange). Elles se situent entre les naines jaunes (analogues au Soleil) et les naines rouges. Elles ont des masses de l’ordre de 0,5 à 0,8 fois celle du Soleil et des températures de surface comprises entre 3900 et 5 200 K.

7) Type M

Les étoiles de classe M sont les plus nombreuses et possèdent une température de surface de 2 500 à 3 900 K. Toutes les naines rouges, soit 80 % des étoiles existantes, sont de ce type, comme par exemple Proxima Centauri. Bételgeuse (géante rouge), de même que les étoiles variables de type Mira sont également de ce type. Leur spectre montre des raies correspondant à des molécules (CN, CH, CO, TiO, VO, MgH, H₂, etc.) et des métaux neutres, les raies du monoxyde de titane TiO peuvent être très intenses et les raies de l’hydrogène en sont généralement absentes.

Spectre d’une étoile de type M0III

Spectre d’une étoile de type M6V

Le cas des naines rouges

Représentation d’une naine rouge

En astronomie, une étoile rouge de la séquence principale, appelée communément naine rouge, est une étoile de type spectral M V (lire « M cinq »), c’est-à-dire une étoile appartenant à la séquence principale (classe de luminosité V) de type spectral M (étoile rouge). Les étoiles K dites tardives (naines oranges les plus froides) sont parfois incluses parmi les naines rouges. Ces étoiles sont peu massives et de température peu élevée. Ayant une masse comprise entre 0,075 et 0,4 masse solaire et une température inférieure à 4 000 K en surface, ce sont des étoiles peu lumineuses, les plus grosses d’entre elles émettant de l’ordre de 10 % de la luminosité solaire. En dessous de 0,075 masse solaire, on a affaire à un objet substellaire, naine brune ou géante gazeuse. La limite entre étoile naine rouge et naine brune de type spectral M est généralement au niveau du type M 6.5. Les naines rouges seraient de loin les étoiles les plus nombreuses de l’Univers. Les modèles stellaires actuels les décrivent comme entièrement convectives, c’est-à-dire que l’hydrogène est constamment brassé par convection dans l’ensemble de l’étoile de sorte que l’hélium issu de la réaction proton-proton au cœur de l’astre ne peut s’y accumuler. Les naines rouges pourraient ainsi briller de façon relativement constante pendant des centaines de milliards d’années, c’est-à-dire plusieurs dizaines de fois l’âge de l’Univers, ce qui signifie que toutes les naines rouges actuelles n’en seraient qu’au début de leur existence.

Découverte

Les premières naines rouges ont été découvertes au XX^e siècle, respectivement en 1915 pour Proxima du Centaure et en 1916 pour l’étoile de Barnard par l’astronome américain Edward Emerson Barnard.

L’étoile de Barnard comparée au Soleil et à Jupiter

Masse et rayonnement

Elles sont de type spectral « K » ou « M ». Elles ont une masse comprise entre 8 et 40 % celle du Soleil (voire 60 % au maximum), et une température de surface plus basse que 3 500 K. Leur luminosité peut être très variable mais est grandement inférieure à celle du Soleil. Celle-ci peut aller de moins de 0,001 % de celle du Soleil jusqu’à 3 ou 4 % au maximum pour les plus volumineuses. Ce sont des étoiles entrées dans la séquence principale, très peu massives, voire à la limite entre un objet substellaire (naine brune) et une étoile. En raison de leur faible masse, leur température centrale n’est pas très élevée. Il faut faire la différence avec un autre type d’étoiles qui pourraient être appelées aussi naines rouges : des cadavres stellaires d’étoiles peu massives, des naines blanches dont la lumière a décru au fil des milliards d’années. Il semblerait que les naines blanches ne se soient pas refroidies suffisamment pour rayonner dans le rouge, et ainsi devenir des « naines rouges » et a fortiori des « naines noires ».

Cycle de vie

Elle ne permet que des réactions de fusion nucléaire du type chaîne proton-proton et la conversion de l’hydrogène en hélium s’y effectue à un rythme très lent. Par conséquent, leurs réserves en hydrogène s’épuisent lentement. Ces étoiles possèdent donc une durée de vie bien plus longue que le Soleil, estimée entre quelques dizaines et 1 000 milliards d’années. L’énergie produite au centre des naines rouges est transportée vers la surface uniquement par convection en raison de l’opacité de leur milieu intérieur. À la différence du Soleil et d’autres étoiles plus massives, l’hélium ne s’accumule donc pas au centre de l’étoile, mais circule à l’intérieur de celle-ci. Elles peuvent donc consommer une plus grande proportion d’hydrogène. À cause de leur faible température (du fait également de leur petite masse), les naines rouges n’arrivent jamais au stade où les autres étoiles commencent la fusion de l’hélium et ne deviennent donc jamais des géantes rouges. Elles se contractent et s’échauffent lentement jusqu’à ce que tout leur hydrogène soit consommé. Dans tous les cas, il ne s’est pas encore passé suffisamment de temps depuis le Big Bang pour que quiconque ait pu observer la séquence terminale d’une naine rouge. Un mystère encore non résolu à ce jour est l’absence de naines rouges dépourvues de métaux (en astronomie un métal est un élément plus lourd que l’hydrogène et l’hélium). En effet la théorie du Big Bang prédit que les étoiles de la première génération ne devraient contenir en leur sein que de l’hydrogène, de l’hélium ainsi que du lithium à l’état de trace. Si cette première génération d’étoiles comportait des naines rouges, on devrait en observer aujourd’hui, mais ce n’est pas le cas. L’explication privilégiée actuellement est que seules des étoiles très massives et appartenant à la population III ont pu se former en l’absence d’éléments lourds dans l’univers. Ces étoiles, d’une durée de vie très brève, ont relâché dans le milieu interstellaire des éléments lourds qui ont permis par la suite la formation de naines rouges.

Présence dans la Voie lactée

Les naines rouges sont probablement les étoiles les plus nombreuses de l’Univers.

Proxima du Centaure, l’étoile la plus proche de nous, ou l’étoile de Barnard (2^e système à moins de 6 années-lumière, solitaire comme le Soleil) sont des naines rouges, de même que vingt autres parmi les trente étoiles les plus proches, comme l’étoile Wolf 359 par exemple, ou encore la composante principale de WISE 0720-0846 (dite l’étoile de Scholz) découvert en 2013.

Elles représenteraient 80 à 85 % des étoiles de notre galaxie, ce qui correspondrait environ à « 160 milliards sur les 200 milliards d’étoiles dans la Voie lactée ».

–

35) Groupes de galaxies, amas, superamas

Les galaxies vivent rarement seules, elles font souvent partie de ce qu’on appelle un amas de galaxies.

I – Le Groupe Local

Ainsi, notre galaxie, la Voie Lactée, fait partie d’un amas qu’on appelle le « Groupe Local ». Ce groupe est constitué d’une soixantaine de galaxies, liées entre elles par la gravitation. Certaines de ces galaxies sont très grandes comme la galaxie d’Andromède et la Voie Lactée, d’autres sont plus petites voire même très petites. Le diamètre du groupe local est d’environ 10 millions d’années-lumière.

Le groupe local subira, dans environ 4 milliards d’années, la fusion des deux principales galaxies qui le composent : la Voie Lactée ainsi que la galaxie d’Andromède (M31). Ce qui résultera sera une très grande galaxie elliptique. Les autres galaxies proches comme celle du Triangle (M33), deviendront les satellites de la grande galaxie finale.

↑ Le Groupe Local

Composants notables du Groupe Local :

La galaxie d’Andromède se situe à 2,54 millions d’années-lumière, aurait un diamètre de 220.000 AL (3,18 ° d’angle > 6 fois la pleine Lune). Elle contiendrait 1.000 milliards d’étoiles mais aurait une évolution plus calme que la Voie Lactée par une moins grande quantité d’étoiles jeunes. Son trou noir supermassif aurait une masse de 110 à 230 millions de masses solaires. Par comparaison, Sagittarius A, le trou noir supermassif de la Voie Lactée a une masse supposée d’à peine 4 millions de masses solaires.

La galaxie la plus proche de nous est la galaxie naine du Grand Chien, à 25.000 AL avec seulement 1 milliard d’étoiles et est très déformée par la gravité de la Voie Lactée. D’autres galaxies sont également plus proches de la Voie Lactée que les Nuages de Magellan (ex : galaxie naine du Sagittaire).

Les nuages de Magellan :

Le Grand Nuage de Magellan, à 160.000 AL, contient environ 30 milliards d’étoiles.
Le Petit Nuage de Magellan, à 197.000 AL, contient environ 3 milliards d’étoiles.

Ces 2 galaxies irrégulières ne seraient pas en orbite autour de la Voie Lactée. Elles ont une vitesse trop grande pour cela. Des indices suggèrent désormais clairement que les nuages de Magellan ont toujours mené une existence bien plus indépendante que supposée. D’abord, ils sont beaucoup plus lumineux que les autres galaxies satellites de notre Voie lactée – au point d’attirer l’attention d’observateurs dépourvus d’instrument optique. Ils sont brillants car ils sont proches de nous et contiennent un grand nombre d’étoiles. Les satellites connus de la Voie lactée abritent chacun jusqu’à 10 millions d’étoiles. Le Petit Nuage de Magellan en renferme quelque 3 milliards, et le Grand, peut-être 30 milliards. Ensuite, les nuages ne ressemblent pas aux galaxies naines sphéroïdales irrégulières qui gravitent à proximité de la Voie lactée et d’autres galaxies spirales majeures. Il s’agit plus vraisemblablement de galaxies autrefois lointaines ; elles ne se seraient assez rapprochées que tout récemment de notre galaxie pour être perturbées par son champ gravitationnel.

D’après une étude de 2007, les mesures ont révélé que la vitesse des nuages de Magellan est trop rapide pour correspondre à des objets en orbite autour de notre galaxie. Cela semble indiquer que ces galaxies naines sont uniquement de passage dans la région occupée par la Voie lactée. En 2006, à l’aide du télescope spatial Hubble, des astronomes ont mesuré le mouvement des nuages de Magellan. Ils ont observé leur déplacement par rapport à des quasars situés à des milliards d’années-lumière plus loin (constituant ainsi un fond à peu près stationnaire dans cet univers où rien ne reste vraiment immobile). Ces mesures semblent indiquer que les nuages suivent des orbites longues excentriques. Leurs trajectoires ne les auraient conduits dans le voisinage de notre galaxie qu’une seule fois auparavant depuis la naissance de l’univers.

II – L’Amas de la Vierge

Le Groupe local forme un ensemble considéré comme typique de quelques dizaines de galaxies. Cet ensemble interagit faiblement avec ses voisins, tels le groupe IC 342/Maffei, le filament du Sculpteur ou le nuage des Chiens de Chasse. Tous sont situés en périphérie d’un amas de galaxies relativement massif, appelé amas de la Vierge. Cet amas abrite notamment la galaxie elliptique géante M87 d’un diamètre de 490.000 années-lumière. M87 a, en son centre, un trou noir supermassif d’environ 6,6 milliards de masses solaires dont le diamètre correspond à environ à l’orbite de Pluton autour du Soleil. M87 est accompagnée de 12.000 à 13.000 amas globulaires (contre 150 à 200 pour la Voie Lactée).

L’amas de la Vierge regroupe le Groupe Local, son diamètre serait de 8° d’angle (taille réelle inconnue) et regroupe 1.300 à 2.000 galaxies

III – Le Superamas Local

L’amas de la Vierge est lui-même le centre d’une structure plus vaste appelée superamas de la Vierge (qu’on préfère appeler désormais superamas Local pour éviter des confusions). L’appartenance au sens strict du Groupe local à l’Amas de la Vierge est ambiguë du fait de sa distance à celui-ci. Le Groupe local s’éloigne aujourd’hui de l’amas de la Vierge (du fait de l’expansion de l’Univers), mais il n’est pas exclu que la proximité de ce dernier et la masse du Superamas local dans sa totalité soient à terme suffisantes pour retenir le Groupe local et le faire tomber sur lui.

Le Superamas Local est constitué de deux éléments : un disque et un halo. Le disque a plus ou moins la forme d’une crêpe et contient 60 % des galaxies lumineuses du superamas. Le halo comprend beaucoup d’objets allongés et comprend donc les 40 % d’éléments restants.

Le superamas Local aurait un diamètre de 200 millions d’années-lumière et le « disque » contient 3 nuages de galaxies : l’Amas de la Vierge, le nuage des Chiens de Chasse et le Nuage de la Vierge II. L’amas de la Vierge est situé en son centre. Le « halo » est constitué de plusieurs nuages allongés pointant vers l’amas de la Vierge.

Le superamas local comporte environ 10.000 galaxies réparties en une centaine d’amas.

À partir de l’effet gravitationnel du superamas sur le mouvement des galaxies qui le constituent, on peut estimer que sa masse totale est environ 10¹⁵ masses solaires, soit 2 × 10⁴⁶ kg. Comme sa luminosité est bien trop faible par rapport au nombre d’étoiles qui le composent, on suppose qu’une grande partie de sa masse est constituée de matière noire. Une anomalie gravitationnelle, le Grand attracteur, se situe près de l’amas de la Règle et attire vers lui l’intégralité du Superamas Local.

IV – Laniakéa

Laniakéa (« horizon céleste immense » en hawaïen), avec un diamètre de 520 millions d’années-lumière a été découvert en 2014 et regroupe 3 superamas qui convergent vers le « Grand Attracteur ».

Le grand attracteur serait une anomalie gravitationnelle dans l’espace intergalactique, d’une taille d’une centaine de millions d’AL. Il se trouve derrière le plan galactique de la Voie Lactée.

Laniakéa contiendrait plus de 100.000 grandes galaxies et plus d’un million de petites…

Il contient notamment :

Le Superamas de la Vierge, qui contient la Voie lactée et donc la Terre.
Le Superamas de l’Hydre-Centaure où se trouve le Grand attracteur.
Le Superamas du Paon-Indien

Les superamas voisins de Laniakea sont le superamas de Shapley, le superamas d’Hercule, le superamas de la Chevelure de Bérénice et le superamas de Persée-Poissons. Les bords des superamas et de Laniakea n’étaient pas clairement connus au moment de la définition de Laniakea.

Une tranche du Superamas Laniakea dans le plan équatorial supergalactique. Les nuances de couleur représentent des valeurs de densité de matière avec en rouge la haute densité et en bleu les vides. Les galaxies individuelles sont montrées comme des points blancs. On observe en blanc des courants de galaxies se déversant dans le bassin d’attraction du Laniakea, tandis que des courants en bleu foncé s’éloignent de ce bassin local et permettent de séparer notre continent de ceux voisins. Le contour orange inclut les limites extérieures de ces courants. Le point bleu foncé à l’extrémité d’un bras blanc indique la localisation de la Voie Lactée. Ce domaine a une mesure de 500 Millions d’années-lumière de diamètre et inclut ~1017 M⊙ (100 millions de millards de masses solaires). © Cosmic Flows

–

36) Étoiles filantes, Radiant, Météores, Bolides, etc.

Rappelons d’abord la signification précise de quelques mots, dont trois sont proches les uns des autres, mais de sens très différents : Météoroïde, Météore, Bolide et Météorite. L’Union Astronomique Internationale les a définis très précisément :

a) un météoroïde est un objet céleste dont la masse est comprise entre 10^-9 et 10⁸ kg avec un diamètre inférieur à 1 mètre, qui circule à plus de 85 km d’altitude au-dessus de la Terre. La fourchette est large car la masse est donc comprise entre 1 milliardième de kg (ou un millionième de gramme) et 100 millions de kg (ou 100.000 tonnes). Ces objets viennent presque toujours des comètes ou des astéroïdes.

b) un météore n’est pas un objet, mais seulement le phénomène lumineux qu’un objet provoque en entrant dans l’atmosphère. Un météoroïde entrant dans l’atmosphère engendrera une traînée lumineuse appelée météore entre 50 et 85 km d’altitude.

c) un bolide n’est pas non plus un objet, c’est un météore dont la trace lumineuse très importante de magnitude inférieure à -4 (identique ou supérieure à celle de Vénus), entre 12 et 80 km d’altitude, avec ou sans explosion (airburst) dans l’atmosphère. Le météoroïde à l’origine de cet objet est de taille plus importante que ce qui provoque une simple étoile filante.

d) une météorite est seulement la partie (ou les parties) d’un météoroïde qui percute le sol de la Terre. Un gros météoroïde, en entrant dans l’atmosphère, va se réchauffer considérablement. Il pourra disparaître complètement ou se briser (ou pas) en plusieurs morceaux plus petits. La ou les météorites sont exclusivement la (ou les) partie(s) du météoroïde qui arrive(nt) au sol.

Une étoile filante est le phénomène lumineux qui accompagne l’entrée dans l’atmosphère d’un corps appelé météoroïde. Il s’agit d’un petit corps circulant dans l’espace à une vitesse pouvant atteindre 42 km/s dans un référentiel lié au Soleil, lorsque son orbite croise celle de la Terre. Cette traînée lumineuse est causée par la vaporisation du corps et l’ionisation de l’air sur sa trajectoire, le météoroïde laissant derrière lui un sillage de gaz très chaud, ionisé et lumineux que l’on nomme un plasma. L’échauffement à l’origine du plasma est principalement dû à la compression de l’atmosphère en avant du corps supersonique et non à la friction.

L’étoile filante est due à une fine poussière cosmique qui est vaporisée entièrement avant d’atteindre le sol tandis que le bolide (causé par un météoroïde de masse et taille importantes) est perçu comme un disque lumineux intense lors de la rentrée atmosphérique du météoroïde, lequel peut se fragmenter ou atteindre le sol, devenant dans ce dernier cas une (ou plusieurs) météorite(s).

Les essaims ou pluies d’étoiles filantes.

C’est quand la Terre passe (sur son orbite) dans les débris issus de la queue d’une comète que vont se produire des étoiles filantes, provoquées par l’entrée de ces débris dans l’atmosphère terrestre : ces débris (de la taille d’un grain de sable à celle d’un petit pois) vont brûler en rentrant dans l’atmosphère à des vitesses allant de 11 à 72 km/s, vitesses hypersoniques supérieures à Mach 5. Sauf exceptions, les étoiles filantes n’ont généralement rien à voir avec des astéroïdes. Il y a des moments dans l’année terrestre où la Terre va passer à un endroit où une comète a laissé des débris. Comme la Terre passe au même endroit tous les ans à la même date, on peut prédire des « pics » dans le nombre d’étoiles filantes. Ces étoiles filantes semblent provenir d’un même point dans le ciel, le radiant.

La pluie d’étoiles filantes la plus connue (mais il y en a d’autres) est celle qui va environ du 23 juillet au 20 août (maximum 12/13 août). On appelle cela les « Perséides » car le « radiant » (l’endroit d’où semblent venir ces étoiles filantes) se situe dans la constellation de Persée. Cette période correspond aux débris laissés par la comète Swift-Tuttle découverte en 1862. Elle est repassée en 1995 et ne repassera pas avant juillet 2126. A chaque passage dans ces débris la Terre « nettoie » un peu les particules de la comète, ce qui fait qu’il y aura de moins en moins d’étoiles filantes dans les perséides au fil des années… jusqu’à ce que la comète repasse près de nous, mais rien ne dit qu’elle repassera au même endroit, les orbites des comètes étant souvent modifiées par les perturbations gravitationnelles provoquées par les planètes (essentiellement Jupiter) et surtout par le Soleil.

On recense plusieurs dizaines d’essaims (environ 75 dans l’année). Les noms de ces pluies d’étoiles filantes sont majoritairement dérivés de la constellation où se trouve leur radiant. Chaque essaim se produit chaque année à la même période avec une intensité variable.

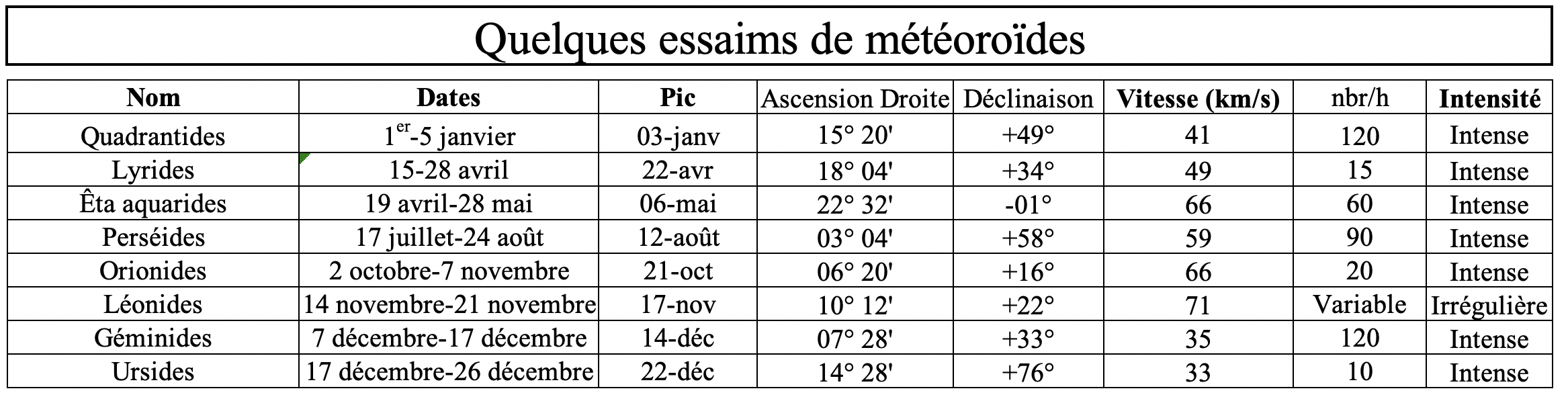(Les Géminides sont une exception. Ces pluies ne sont pas causées par une comète, mais par l’objet (3200) Phaéton, qu’on estime faire partie de la famille d’astéroïdes Apollon)

Ainsi, par exemple, la pluie de météores des Léonides se produit quand la Terre traverse l’orbite de la comète 55P/Tempel–Tuttle et que les débris suivant cette comète sont des météoroïdes qui se subliment et entrent dans l’atmosphère de la Terre.

Lors d’une pluie de météores, on peut apercevoir typiquement entre 5 et 50 météores en une heure. Ces météores sont dus aux météoroïdes qui entrent dans l’atmosphère à la même vitesse (qui varie de 11 à 72 km/s). Le phénomène peut durer de quelques heures à plusieurs jours, et revient habituellement annuellement.

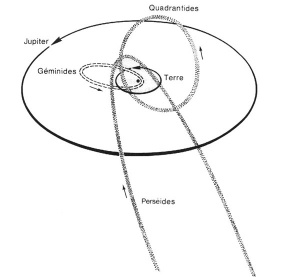
Trajectoires des 2 comètes qui provoquent les pluies d’étoiles filantes (Perséides et Quadrantides) et de l’astéroïde (3200) Phaeton qui provoque les Géminides.

Les météores ne proviennent pas toujours nécessairement d’un essaim. Il arrive aussi que des météores dits « sporadiques » surviennent. Ce sont des météores isolés qui ne sont pas reliés à un nuage cométaire.

La vitesse à laquelle les débris de comètes entrent dans l’atmosphère terrestre est très variable car elle dépend de trois paramètres :

La vitesse de la comète originaire des débris (autour de 30 à 50 km/s), lesquels ont environ la même vitesse et la même direction que celles de la comète.
La vitesse de la Terre dans son orbite annuelle autour du Soleil (en moyenne 30 km/s).
Dans un référentiel commun en 3D (par exemple celui du Soleil), la direction des débris cométaires par rapport à la direction de la Terre au moment de la rencontre.

Si les débris sont dans la direction directement opposée à celle de la Terre, les vitesses vont d’additionner. S’ils sont dans la même direction elles vont se soustraire. Enfin si les débris et la Terre viennent de directions différentes (une infinité de possibilités) les vitesses vont s’agréger en fonction de leurs vitesses propres et surtout en fonction de l’angle d’attaque entre la direction des débris et celle de la Terre.

Le radiant

Radiant est un terme d’astronomie désignant le point de la voûte céleste d’où, par un effet d’optique dû à la perspective, l’essentiel des « étoiles filantes » provenant d’un même essaim semble venir. Habituellement, lorsque ce point est situé dans une constellation, l’essaim prend un nom dérivant de cette dernière. Ainsi, par exemple, le radiant de l’essaim des Orionides se situe dans (ou près) de la constellation d’Orion.

Radiant des Perséides

Le fait que tous les météores d’un essaim semblent provenir d’un même point de la voûte céleste est dû au même effet d’optique que l’illusion que l’on a, dans une voiture roulant vite sous la pluie ou la neige, de voir l’ensemble des gouttes de pluie ou des flocons de neige provenir d’un point situé exactement dans la direction où la voiture se déplace. Autrement dit, il s’agit du point de fuite associé à la direction d’arrivée des météoroïdes, relative à la Terre. Dans le cas d’une pluie d’étoiles filantes, cet effet d’optique est donc lié au mouvement de la Terre qui rencontre sur sa trajectoire l’essaim de grains de poussière qui leur donne naissance.

Plus précisément, cette poussière continue son chemin dans la direction du parcours de la comète et, lorsque la Terre se déplace au travers de ces débris, une pluie de météores en résulte. Puisque tous les débris se déplacent à peu près dans la même direction, les météores générés par les météoroïdes qui entrent en collision avec l’atmosphère « pointent » tous, plus ou moins, dans la direction de la trajectoire de la comète.

Quelques “pluies d’étoiles filantes” avec leurs radiants bien visibles :

Les Perséides

Les Géminides

Les Orionides

–

37) Année Besselienne

En astronomie, l’année besselienne (parfois orthographiée année bessélienne) correspond à l’intervalle de temps entre deux années tropiques mesurées depuis un point où l’ascension droite du Soleil est de 280 degrés (ou mieux dit 18 h 40 min 0 s). Cette longitude correspond approximativement à la position du Soleil vu depuis la Terre au 1^er janvier.

Le nom d’année besselienne est donné en l’honneur du mathématicien et astronome germanique Friedrich Wilhelm Bessel.

L’année besselienne correspond à 365,242198781 jours (la durée d’une année tropique), soit 31 556 925,9747 secondes. Cela représente 674,025 3 secondes de moins que l’année julienne, définie comme correspondant à 365,25 jours exactement.

La définition de l’année besselienne permet de construire une époque, dont l’année commence lorsque l’ascension droite du Soleil égale 280 degrés. L’époque basée sur l’année besselienne est précédée de la lettre B (B1875.0, par exemple). De nos jours, les époques sont construites à partir d’un instant de référence (noté J2000.0), correspondant approximativement au moment du midi du méridien de Greenwich au 1^er janvier 2000. L’ascension droite du Soleil à cet instant-là n’étant pas exactement égale à 280, et les durées des années besseliennes et juliennes différant de plusieurs minutes, les époques juliennes et besseliennes ne sont pas identiques. Ainsi l’époque J2000.0 correspond-elle à l’époque B2000.00127751.

–

38) Etoiles Wolf-Rayet

Une étoile Wolf-Rayet (souvent abrégé en étoile WR) est une étoile chaude de plusieurs dizaines de masses solaires, qui durant une phase relativement brève (de l’ordre du million d’années) suivant sa séquence principale, se met à expulser la matière entourant son noyau sous forme de vents stellaires à haute vélocité, laissant celui-ci à nu, avant d’exploser en supernova.

Elles furent découvertes en 1867 par Charles Wolf et Georges Rayet, de l’Observatoire de Paris. Wolf et Rayet avaient observé, dans trois étoiles de la constellation du Cygne, d’étranges raies en émission d’origine alors inconnue. On pense aujourd’hui que les étoiles Wolf-Rayet sont les descendantes des étoiles de type spectral O ou B, c’est-à-dire les étoiles les plus massives des populations stellaires (qui ont une masse comprise entre 9 et 80 à 315 masses solaires).

On parle d’une « étoile Wolf-Rayet » pour dire une étoile « de type Wolf-Rayet », plutôt qu’une « étoile de Wolf-Rayet » (comme on parle de l’« étoile de Barnard »).

Les étoiles Wolf-Rayet ne sont, en grande majorité, plus sur la séquence principale, c’est-à-dire que la combustion en leur cœur n’est plus celle de l’hydrogène, mais celle d’autres éléments, à savoir, par étapes, l’hélium, puis le carbone, l’oxygène, etc. On parle donc parfois du « stade (évolutif) Wolf-Rayet » ou d’une étoile montrant des caractéristiques Wolf-Rayet. Une autre caractéristique de ces étoiles est leur vent stellaire si important qu’il en devient optiquement épais, ne laissant plus percevoir le spectre de l’étoile elle-même. On ne peut alors pas non plus parler de surface (hydrostatique), contrairement aux étoiles « normales », de plus faible masse, comme le Soleil.

Les scientifiques estiment aujourd’hui qu’il en existerait environ 6 000 sur les 200 à 400 milliards d’étoiles que contient la Voie Lactée. La plus massive jamais observée, R136a1, atteint une masse de 315 M☉ et se situe dans la constellation de la Dorade.

Image du télescope spatial Hubble de la nébuleuse M1-67 autour de l’étoile Wolf-Rayet WR124.

Découverte

Wolf et Rayet décrivent ainsi leur découverte :

« Parmi les nombreuses étoiles dont la lumière a été étudiée à l’aide d’un prisme, on n’en connaît qu’une seule, Gamma de Cassiopée, dont le spectre offre constamment des lignes brillantes. Nous avons l’honneur de signaler à l’Académie l’existence de semblables lignes dans trois étoiles de la constellation du Cygne… Leur spectre se compose d’un fond éclairé dont les couleurs sont à peine visibles. Tous trois présentent une série de lignes brillantes. L’identification des lignes lumineuses de ces étoiles avec celles des spectres des gaz incandescents nous a été impossible… » (Comptes rendus de l’Académie des sciences, 1867, vol 65, p. 292)

La présence de ces raies en émission est longtemps restée mystérieuse, d’autant que l’on découvrira au début du XX^e siècle leur largeur énorme. Dans les années 1960, les étoiles WR ont tour à tour été identifiées à des étoiles en formation (dites de pré-séquence principale), à des étoiles instables, au résultat d’interactions dans les binaires, et à des étoiles évoluées ayant perdu une masse conséquente. Cette dernière hypothèse est celle qui a rassemblé le plus de suffrages, le scénario d’évolution étant alors surnommé « scénario de Conti » d’après les travaux de Peter Conti et de ses collègues, bien qu’il ne soit pas le premier à l’avoir proposé (cf. travaux de Rublev en 1965).

Caractéristiques principales

Les étoiles WR éjectent beaucoup de matière, par le biais d’un vent stellaire. Celui-ci est beaucoup plus fort que le vent solaire : la perte de masse atteint en effet un taux de 10⁻⁵ masse solaire par an pour les WR contre 10⁻¹⁴ pour le Soleil ; la vitesse du vent est également bien plus grande, avec environ 2 000 km/s pour les WR.

C’est dans ce vent que naissent les raies larges en émission : le spectre stellaire ne dévoile pas la surface de l’étoile, comme c’est le cas pour le Soleil, mais les couches du nuage entourant celle-ci. La perte de masse ayant amené en surface des zones enrichies en éléments lourds par les réactions nucléaires internes, le spectre est clairement enrichi en métaux (métallicité élevée). Si les raies dominantes proviennent de l’azote, on parle d’étoile WN ; pour le carbone d’étoiles WC et pour l’oxygène d’étoiles WO.

Ces étoiles WR sont assez rares : on en connaît actuellement 298 dans notre Galaxie et une centaine dans les Nuages de Magellan.

La fréquence de binaires dans les Nuages de Magellan

Les Nuages de Magellan sont deux galaxies irrégulières naines au voisinage de notre propre Voie lactée. Elles ont la particularité d’avoir une métallicité moindre que celle dans le voisinage solaire (laquelle sert de valeur de référence et est notée Z_o). La métallicité a un effet direct sur le taux de perte de masse, et donc la capacité des étoiles massives à devenir des étoiles Wolf-Rayet. Dans les années 1990, des études de populations des étoiles Wolf-Rayet ont montré qu’il était nécessaire dans les modèles de doubler de manière artificielle le taux de perte de masse pour expliquer le nombre d’étoiles Wolf-Rayet dans les Nuages de Magellan. Bien conscients que la solution de doubler le taux de perte de masse était ad hoc, il a été proposé que la fréquence d’étoiles Wolf-Rayet binaires de courte période soit plus grande à faible métallicité. Dans ce cas, l’étoile massive voyait son potentiel gravitationnel diminué par la présence d’un compagnon proche, ce qui devait lui permettre de perdre plus de matière que lors de l’évolution d’une étoile simple.

Cependant, des études ultérieures sur la quasi-totalité des 12 étoiles Wolf-Rayet du Petit Nuage de Magellan et des 134 du Grand Nuage de Magellan ont montré que seulement 30 à 40 % des étoiles étaient effectivement des binaires à courte période, comme les autres étoiles et comme dans notre propre galaxie. En d’autres termes, il fallait trouver une autre explication.

L’explication donnée aujourd’hui n’est pas encore complète, mais repose sur deux ingrédients : une vitesse de rotation plus élevée à faible métallicité, et un vent structuré (clumpy, ou « poreux »).

Classification spectrale

Une étoile est dite Wolf-Rayet si elle montre certaines caractéristiques spectrales précises dont la plus importante est la présence de raies d’émission larges principalement d’hélium, mais aussi d’azote, et parfois de carbone et d’oxygène. La force relative et la présence ou absence de certaines raies permet de classifier l’étoile Wolf-Rayet. La classification des étoiles Wolf-Rayet est un point toujours délicat puisque les caractéristiques spectrales observables sont le reflet de l’état du vent stellaire, et non directement de la « surface » de l’étoile ou de son cœur, inaccessible.

On distingue trois grandes clas’es d’étoiles Wolf-Rayet : les étoiles « WN », riches en azote (N) ; les étoiles « WC », riches en carbone © ; et les étoiles « WO » pour lesquelles le rapport entre l’oxygène (O) et le carbone © est strictement inférieur à un. De plus, on distingue encore les étoiles WN en deux sous-classes : les étoiles WNL (pour WN late en anglais, c’est-à-dire tardive), et les étoiles WNE (pour early en anglais, c’est-à-dire précoce). Cette distinction est aussi valable pour les étoiles WC mais très peu utilisée. Pour être complet, précisons que la classification précise des étoiles Wolf-Rayet se décompose entre 10 sous-types WN : de WN11 à WN2, et 7 sous-types WC : de WC9 à WC2 (mais les étoiles WC sont principalement WC9 ou WC4). La classification précise dépend de la mesure précise des forces relatives de certaines raies, comme définie dans le système de classification de Smith, Shara et Moffat (1996, MNRAS, 281, 163). Enfin, les étoiles WN11 à WN6 sont considérées comme des WNL, et les étoiles WN5 à WN2 sont considérées comme WNE.

Ceci peut paraître inutilement compliqué, mais est en fait la conséquence, comme souvent en astronomie, de raisons « historiques ». La plupart du temps, les astronomes classifient avant de comprendre. On peut utiliser cette classification pour parler de chemins évolutifs. Globalement, le chemin évolutif d’une étoile massive s’écrit ainsi :

O → RSG/LBV → WNL → WNE → WC → SN

où O désigne une étoile de type O, RSG (Red Supergiant) désigne une étoile supergéante rouge, LBV (Luminous Blue Variable) désigne une étoile de type LBV, et SN désigne une supernova. Toutes les étoiles massives ne traversent pas toutes les phases. Cela dépend de trois paramètres initiaux : la masse, la métallicité et la vitesse de rotation.

Spectre de l’étoile Wolf-Rayet WR137, de type spectral WC7

Évolution

Les étoiles Wolf-Rayet ont comme progéniteurs les étoiles initialement les plus massives, les étoiles O. Des étoiles moins massives ne forment pas d’étoiles Wolf-Rayet. Bien que la masse initiale minimum pour former une étoile Wolf-Rayet soit connue (environ 15 à 25 masses solaires — cela dépend de la métallicité ambiante), on ne sait pas du tout jusqu’à quelle limite supérieure la masse initiale peut aller, s’il y en a une. Une fois que la combustion de l’hydrogène est terminée (fin de la séquence principale), le cœur se contracte, l’enveloppe se dilate et l’étoile passe par un stade intermédiaire qui peut soit être stable (RSG — supergéante rouge) soit instable (LBV). Il se peut que la combustion en couche de l’hydrogène se fasse pendant ce stade.

Ensuite, si l’étoile est suffisamment massive, la fusion de l’hélium dans le cœur démarre. Puisque cette combustion est largement plus puissante que celle de l’hydrogène, elle dégage beaucoup plus d’énergie, et est à l’origine d’un vent opaque et dense. Puisque le vent est opaque (ou optiquement épais) il n’est plus possible de distinguer la surface, et l’étoile est une Wolf-Rayet. Le vent d’une Wolf-Rayet est si fort (jusqu’à 10^-5 masse solaire par an) qu’il enlève petit à petit toutes les couches supérieures (riches en hydrogène) de l’étoile. Tant que l’étoile possède encore de l’hydrogène dans le vent, elle apparaît comme une WNL. Une fois que l’hydrogène a disparu, elle devient une WNE.

Les produits de la fusion de l’hélium sont principalement le carbone et l’oxygène. Puisque les couches supérieures de l’étoile disparaissent, le carbone devient visible, et l’étoile devient une WC. Une fois que la fusion de l’hélium dans le cœur est terminée, c’est la fusion du carbone qui commence, dont le produit est principalement l’oxygène. Puis il s’ensuit la fusion de l’oxygène en silicium, et ainsi de suite, jusqu’au fer. La stabilité du fer est telle qu’une fois le cœur de fer atteint, la température dans le noyau de l’étoile n’est pas suffisante pour entamer la fusion de cet élément. L’étoile s’effondre donc sur elle-même et explose en supernova.

Les étoiles les plus massives ?

C’est parmi les étoiles Wolf-Rayet que l’on trouve les étoiles les plus massives de l’univers. Cela peut sembler paradoxal, car s’il s’agit d’étoiles évoluées ayant perdu beaucoup de masse, elles devraient avoir des masses assez faibles. Toutefois, il faut savoir qu’une étoile est classée WR uniquement sur base de l’aspect de son spectre : toute étoile présentant des raies larges en émission est donc classée WR. Parmi ces objets, des « fausses » WR viennent se glisser, des étoiles très lumineuses mais toujours sur la séquence principale – il ne s’agit donc pas d’étoiles évoluées. C’est le cas des records WR 20a, dans l’amas stellaire Westerlund 2, ainsi que NGC 3603 A1, dans l’amas NGC 3603.

Microquasars, sursauts de rayons gamma

Les étoiles Wolf-Rayet peuvent donner naissance à une multitude d’objets astrophysiques intéressants. Cela rend leur étude d’autant plus importante. On peut distinguer principalement deux grandes catégories : les résultats de l’évolution d’une étoile simple, et ceux de l’évolution d’une étoile binaire.

Une étoile Wolf-Rayet qui explose en supernova peut donner naissance à une étoile à neutrons ou un trou noir. L’apparition de l’un ou de l’autre dépend de la quantité de matière qui n’est pas éjectée par l’explosion. Si la masse de l’objet central après l’explosion est plus grande que 1,4 masse solaire, le résultat sera une étoile à neutrons. Si elle est plus grande que trois masses solaires, le résultat sera un trou noir. Il est aussi possible que l’explosion détruise complètement l’étoile, et que toute la matière soit éjectée dans le milieu interstellaire.

Bien que la question de savoir s’il faut ou non une étoile binaire ne soit pas encore résolue, les étoiles Wolf-Rayet sont considérées comme les progéniteurs des fameux sursauts de rayons gamma. Le modèle le plus accepté pour l’instant est le modèle du « collapsar » (du verbe collapse, s’effondrer en anglais). Il décrit comment l’effondrement de l’étoile en trou noir durant la supernova crée un jet à très haute énergie, et produit des rayons gamma.

Les résultats de l’évolution d’une étoile binaire Wolf-Rayet, c’est-à-dire qu’au moins l’une des deux étoiles est une Wolf-Rayet, sont peut-être encore plus intéressants puisqu’encore plus variés. Lorsque l’étoile Wolf-Rayet explose en supernova, il y a deux possibilités pour le système binaire. Soit il se détache, soit il reste attaché. Quand le système se détache, il produit alors une étoile à neutrons ou un trou noir à haute vitesse, qui part se balader dans l’espace interstellaire. La seconde étoile part dans la direction opposée. Des études récentes ont réussi à reconstruire le parcours d’une étoile à neutrons à haute vitesse, et celui d’une étoile massive. Ils ont montré que les deux objets avaient la même origine spatiale, et qu’ils avaient été formés très certainement dans l’amas d’étoiles qui se trouvait entre les deux. Cela a été fait aussi pour un trou noir, bien que cela soit largement plus difficile d’étudier un trou noir isolé dans l’espace.

Si le système reste lié, il acquiert certainement une grande vitesse spatiale due à l’explosion. Cependant, on se retrouve avec un système à courte période contenant une étoile à neutrons ou un trou noir, avec une étoile secondaire. Si l’étoile secondaire est une étoile de faible masse (quelques masses solaires), sa matière est aspirée en direction du trou noir ou de l’étoile à neutrons. Cela crée un disque d’accrétion qui spirale autour de l’objet compact, et produit beaucoup de rayons X. Lorsque l’objet compact est une étoile à neutrons, on parle de binaire X de grande masse (High-Mass X-ray binary ou HMXB). Lorsque l’objet compact est un trou noir, on parle d’un microquasar. Les microquasars sont l’équivalent à l’échelle stellaire des quasars dans les galaxies actives. Dans ces dernières, un tore de poussières et de gaz enveloppe un trou noir de plusieurs millions de masses solaires.

Encore plus étrange : lorsque l’étoile secondaire est une étoile relativement massive, elle évolue naturellement vers le stade d’étoile géante rouge. Son rayon croît alors de manière incroyable (plus d’un facteur 100), et peut alors absorber l’étoile à neutrons. C’est la phase d’évolution avec une enveloppe commune. L’étoile à neutrons spirale alors à l’intérieur de l’étoile géante rouge. En fonction du gradient de densité de l’enveloppe de la géante rouge, les modèles prédisent qu’il est possible que l’étoile à neutrons reste prisonnière à l’intérieur. Le résultat serait que l’étoile à neutrons prenne la place du cœur de l’étoile. On parle alors d’objets de Thorne-Żytkow, des noms des deux premiers qui ont théorisé l’existence de tels objets : Kip Thorne et Ana Zytkow.

Bien que d’autres modèles montrent que ce genre d’objet n’est pas stable à cause d’une perte d’énergie par neutrinos (ce qui provoquerait l’effondrement complet de l’objet en un trou noir), des programmes d’observations ont été lancés pour savoir si les objets de Thorne-Zytkow existaient bel et bien. Il a été proposé dans la littérature que les étoiles Wolf-Rayet de type WN8 soient justement des objets de Thorne-Zytkow. En effet, les WN8 sont caractérisées par le fait qu’aucune d’elle ne soit apparemment une étoile binaire, qu’elles sont souvent en dehors des amas ou des associations, qu’elles possèdent une grande vitesse spatiale, et qu’elles montrent systématiquement un très grand taux de variabilité stochastique aussi bien en photométrie qu’en polarimétrie ou en spectroscopie.

À ce jour, aucune preuve observationnelle n’a permis de savoir si les objets de Thorne-Żytkow existaient, et s’il fallait les trouver parmi les étoiles Wolf-Rayet de type WN8.

–

39) Globules de Bok

Un globule de Bok est un amas sombre de poussières et de gaz du milieu interstellaire au sein duquel peut commencer la naissance des étoiles. Ils sont courants dans les régions HII et ont typiquement une masse d’environ 10 à 50 masses solaires contenue dans un volume d’environ une année-lumière. Ils contiennent de l’hydrogène moléculaire (H₂), des oxydes de carbone, de l’hélium et environ 1 % (en masse) de poussières de silicates. Les globules de Bok conduisent le plus souvent à la formation de systèmes d’étoiles doubles ou multiples.

Les globules de Bok furent observés pour la première fois par l’astronome Bart Bok dans les années 1940. Dans un article publié en 1947, Bok et E.F. Reilly firent l’hypothèse que ces nuages étaient « similaires à des cocons d’insectes » en cours d’effondrement gravitationnel pour former des proto-étoiles à partir desquelles les étoiles et les amas d’étoiles naissent. Cette hypothèse était difficile à vérifier à cause des difficultés d’observation pour comprendre ce qui se passait à l’intérieur d’un nuage dense et sombre qui absorbait toute la lumière visible émise à l’intérieur. Une analyse d’observations faites dans le proche infrarouge publiée en 1990 a confirmé que les étoiles naissaient bien à l’intérieur des globules de Bok.

Des observations ultérieures ont montré que certains globules de Bok contenaient des objets chauds, d’autres des objets Herbig-Haro, et que certains expulsaient du gaz moléculaire. Des études des raies d’émission en ondes millimétriques ont aussi montré l’existence de chute de matière sur une proto-étoile en accrétion.

Les globules de Bok sont encore un sujet de recherche très actif. Connus pour être parmi les objets les plus froids de l’univers naturel (jusqu’à 3 kelvins), leur structure et leur densité demeurent assez mystérieuses. Les méthodes utilisées jusqu’à présent reposent sur la densité de colonne déduite de mesures d’extinction en infrarouge proche et même sur le comptage d’étoiles pour tenter de sonder ces objets plus profondément.

Les globules de Bok sont des nuages denses et froids (quelques degrés K), de gaz et de poussières, contenant de 10 à 50 masses solaires et dont le diamètre est de l’ordre d’une année-lumière. Observés vers 1940 par l’astronome américano-hollandais Bart Bok, celui-ci avait alors émis l’hypothèse qu’il s’agissait de régions subissant un effondrement gravitationnel débouchant sur la formation d’étoiles. Au début des années 90, l’observation en infra-rouge proche a effectivement permis de valider cette hypothèse.

L’Observatoire européen austral (ESO) vient de publier une nouvelle photo provenant du Very Large Telescope, situé au Chili. Celle-ci montre un globule de Bok, c’est à dire un amas de poussière et de gaz interstellaire, nommé CG4, qui est l’un des plus importants de notre galaxie.

Un globule de Bok est donc un amas de poussière, qui pourrait être à l’origine de la formation d’étoiles. Découvert en 1976, CG4 est distante de la Terre de près de 1300 année-lumières, dans la constellation Puppis, et fait montre d’une taille colossale. Elle est en effet souvent affublée de surnoms comme « La gueule de la bête », ou encore « La main de Dieu ». Sa forme rappelle une comète, et sa « tête » mesure près de 1,5 année-lumière de diamètre, tandis que la queue mesure environ 8 année-lumières de long.

Globule de Bok

–

40) Objets Herbig-Haro

En astronomie, les objets de Herbig-Haro (ou parfois simplement objets Herbig-Haro ; en abrégé objets HH) sont de petites nébulosités associées à certaines très jeunes étoiles, qui se forment lorsque de la matière éjectée par ces étoiles naissantes entre en collision avec les nuages de gaz et de poussières environnant, à des vitesses de plusieurs centaines de kilomètres par seconde. Les objets Herbig-Haro sont omniprésents dans les régions de formation stellaire, et bien souvent il est possible d’en observer plusieurs autour d’une même étoile, alignés le long de son axe de rotation.

Ces objets sont des phénomènes éphémères, ayant une durée de vie de quelques milliers d’années tout au plus. Il est possible de les voir évoluer sur une période de temps relativement courte, alors qu’ils s’éloignent de l’étoile dont ils sont issus à travers les nuages de gaz interstellaire. Les observations du télescope spatial Hubble montrent des évolutions complexes en quelques années seulement, certaines parties s’affaiblissant tandis que d’autres s’illuminent, suivant la densité du milieu rencontré.

Les objets Herbig-Haro ont été observés pour la première fois par Sherburne Wesley Burnham à la fin du XIX^e siècle, mais ce n’est que dans les années 1950 que l’on a compris qu’il s’agissait d’un nouveau type de nébuleuse en émission. Les premiers astronomes à les avoir étudiés en détail sont George Herbig et Guillermo Haro, d’où leur nom. Herbig et Haro étudiaient indépendamment la formation des étoiles lorsqu’ils ont analysé ces objets, et ont compris qu’ils étaient la conséquence du processus de formation des étoiles.

Les objets HH1 et HH2 sont séparés d’environ une année-lumière, symétriquement opposés par rapport à la jeune étoile qui éjecte de la matière le long de son axe de rotation.

L’objet Herbig-Haro HH47, vu par le télescope spatial Hubble. La barre d’échelle représente 1.000 ua, soit environ 30 fois la distance Soleil-Neptune.

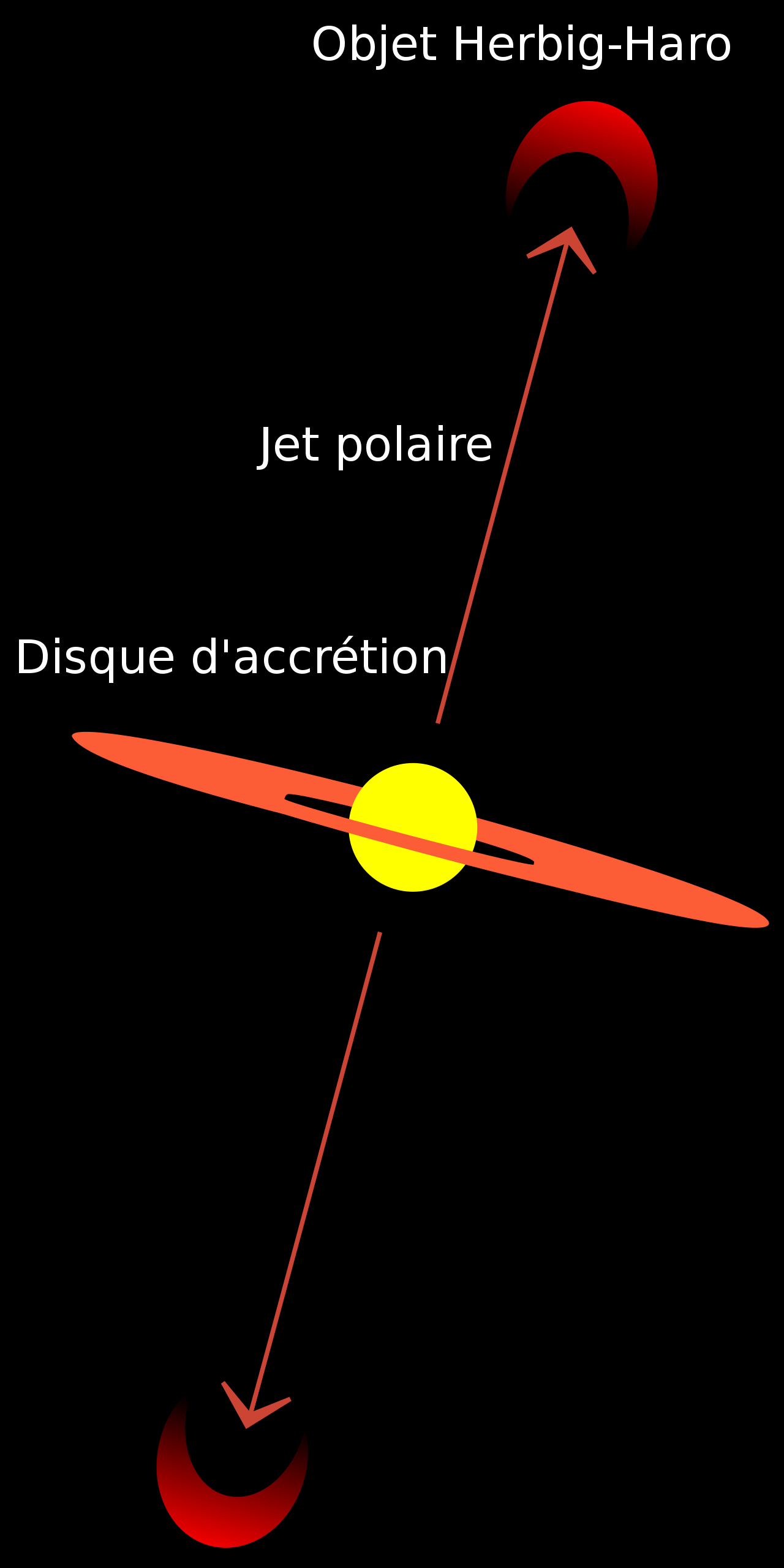Schéma du processus de formation d’un objet Herbig-Haro

Découverte et observations

Le premier objet Herbig-Haro a été découvert par Sherburne Wesley Burnham à la fin du XIX^e siècle : alors qu’il observait l’étoile T Tauri avec la lunette de 900 mm de l’observatoire Lick, Burnham aperçut juste à côté une toute petite nébulosité. Celle-ci fut cataloguée comme une nébuleuse en émission « standard », dénommée « nébuleuse de Burnham » par la suite (désormais HH 255), mais ne fut pas à cette date reconnue comme représentante d’une nouvelle classe d’objets. En revanche, on savait déjà à cette époque que T Tauri était une étoile variable très jeune, prototype d’une classe d’étoiles variables appelées « variables de type T Tauri ». Ces étoiles sont extrêmement jeunes et n’ont pas encore atteint le stade d’équilibre où l’effondrement gravitationnel est compensé par les réactions de fusion nucléaire en leur centre.

À la fin des années 1940, soit cinquante ans après la découverte de Burnham, certaines nébuleuses similaires avaient été observées, la plupart étant si petites qu’on pouvait presque les confondre avec des étoiles. Guillermo Haro et George Herbig menaient alors de façon indépendante des observations sur plusieurs de ces objets. Herbig se pencha à nouveau sur la nébuleuse de Burnham et trouva qu’elle possédait un spectre électromagnétique inhabituel, présentant des raies d’émission très marquées pour l’hydrogène, le soufre ([S II]) et l’oxygène ([O II]), et que d’autres objets, tels que HH 1, HH 2 et 3, présentaient des caractéristiques similaires. De son côté, Haro annonça en 1952-1953 la découverte de nombreux autres objets du même type et montra que tous étaient invisibles en infrarouge.

À la suite de leurs observations, Herbig et Haro se rencontrèrent à un colloque d’astronomie à Tucson en Arizona en 1949. Herbig n’avait pas porté beaucoup d’attention aux objets qu’il avait observés, s’attachant surtout à l’étude des jeunes étoiles proches, mais en prenant connaissance des découvertes de Haro, il décida de mener une étude plus poussée. L’astronome soviétique Viktor Ambartsumian donna alors leur nom actuel à ces objets. À partir de leur proximité avec les étoiles les plus jeunes (âgées de quelques centaines de milliers d’années tout au plus), il suggéra que les objets Herbig-Haro puissent être liés aux premières étapes de la formation des étoiles T Tauri.

Les études qui suivirent montrèrent que les objets HH étaient fortement ionisés, et les premières théories avançaient qu’ils puissent contenir des étoiles chaudes de faible luminosité. Toutefois, l’absence de rayonnement infrarouge provenant de la nébuleuse contredisait cette hypothèse. On imagina plus tard que la nébuleuse pouvait contenir des proto-étoiles, l’énergie libérée au cours du processus d’accrétion devenant la source de photoionisation.

Au fur et à mesure des avancées théoriques et observationnelles, il devint clair que les objets HH étaient engendrés par la matière éjectée par les jeunes étoiles proches, cette matière entrant en collision à des vitesses très élevées avec le gaz du milieu interstellaire.

Au début des années 1980, les progrès techniques permirent aux observations de révéler la forme en jets des objets HH. Ceci conduisit à comprendre que la matière éjectée et qui donne naissance aux objets HH est concentrée en jets bipolaires très fins (collimatés). En effet, les étoiles naissantes sont entourées, pendant les premiers milliers d’années de leur existence, par un disque d’accrétion formé par des restes du nuage de gaz initial. La rotation rapide des parties les plus internes de ce disque engendre l’émission de puissants jets de matière partiellement ionisée perpendiculairement au plan du disque. Lorsque ces jets entrent en collision avec le milieu interstellaire, ils donnent naissance à de petites nébuleuses en émission, dont les objets Herbig-Haro.

Caractéristiques physiques

Le rayonnement émis par les objets Herbig-Haro est dû aux ondes de choc provoquées par la collision avec le milieu interstellaire, mais leurs mouvements sont compliqués. Les observations spectroscopiques du décalage Doppler indiquent que la matière des jets se déplace à des vitesses de plusieurs centaines de kilomètres par seconde, mais les raies d’émission du spectre de ces objets sont trop faibles pour avoir été formées à de telles vitesses de collision. Ceci signifie probablement que la matière avec laquelle les jets entre en collision est également en mouvement, s’éloignant elle aussi de l’étoile centrale, mais à une vitesse inférieure à celle des jets.

L’estimation de la masse totale éjectée nécessaire pour former un objet HH est de l’ordre de une à vingt masses terrestres, soit une quantité relativement faible par rapport à la masse totale de l’étoile elle-même. Les températures observées dans les objets HH sont d’environ 8 000 à 12 000 kelvins, similaires à celles observées dans d’autres types de nébuleuses ionisées, telles que les régions HII ou les nébuleuses planétaires. Ils sont relativement denses, leur densité variant de quelques milliers à quelques dizaines de milliers de particules par centimètre cube, les régions HII ayant par comparaison une densité inférieure à 1 000 particules par centimètre cube en général. Les objets HH sont constitués principalement d’hydrogène et d’hélium, respectivement 75 % et 25 % en masse environ. Moins d’un pour cent de la masse totale de ceux-ci est constitué d’éléments plus lourds, et leur abondance est en général similaire à celle mesurée dans les jeunes étoiles proches.

Auprès de l’étoile source, entre 20 et 30 % du gaz d’un objet HH est ionisé, mais cette proportion a tendance à décroître avec la distance. Ceci implique que le gaz est ionisé dans le jet polaire, et se recombine ensuite alors qu’il s’éloigne de l’étoile, plutôt que d’être ionisé lors de la collision en elle-même. Le choc se produisant à l’extrémité du jet peut toutefois ré-ioniser une partie de la matière, donnant naissance à des « chapeaux » plus brillants à l’extrémité des jets.

L’objet Herbig-Haro HH32 est l’un des plus lumineux que l’on connaisse.

Nombre et distribution

Plus de 450 objets HH ou groupes d’objets sont actuellement répertoriés (2006). Ils sont omniprésents dans les régions de formation d’étoiles, et très souvent présents en groupes. On les observe très souvent auprès des globules de Bok (des nébuleuses obscures contenant des étoiles très jeunes), et ils émanent d’ailleurs souvent de ces globules. Il est fréquent d’en observer plusieurs auprès d’une seule étoile, formant ainsi une sorte de chapelet le long d’une ligne représentant l’axe de rotation de celle-ci.

Le nombre d’objets HH connus a augmenté rapidement ces dernières années, mais on pense généralement que ce nombre ne représente en réalité qu’une très faible proportion de la quantité existant réellement dans la Galaxie. Les estimations suggèrent qu’il en existe jusqu’à 150 000, la grande majorité d’entre eux étant trop éloignés et trop peu lumineux pour pouvoir être résolus avec les instruments actuels. La plupart des objets HH se trouvent à une distance n’excédant pas 0,5 parsec de l’étoile source, certains ayant été observés jusqu’à 1 parsec. Il en existe toutefois un petit nombre se situant à plusieurs parsecs de distance, probablement parce que le milieu interstellaire est très peu dense dans leur voisinage, permettant ainsi à la matière éjectée de voyager beaucoup plus loin avant d’être dispersée.

Mouvement propre et variabilité

Les observations spectroscopiques des objets HH montrent que ceux-ci s’éloignent de l’étoile source à des vitesses variant de 100 à 1 000 km/s. Ces dernières années, le télescope spatial Hubble a permis de mesurer le mouvement propre de plusieurs objets HH, grâce à des observations espacées de plusieurs années.

Lorsqu’ils s’éloignent de leur étoile, les objets HH évoluent de façon significative, variant en luminosité sur des périodes de quelques années seulement. Certains « nœuds » à l’intérieur de l’objet HH peuvent s’éclairer, s’affaiblir ou bien disparaître complètement, tandis que d’autres apparaissent à un endroit différent.

La matière des jets émis par l’étoile n’est pas éjectée en continu mais plutôt par impulsions. Ces pulsations peuvent produire des jets de gaz se déplaçant dans la même direction mais à des vitesses différentes, et les interactions entre ces différents jets produisent à leur tour des ondes de choc.

Etoiles sources

Les étoiles qui se cachent derrière la création des objets Herbig-Haro sont très jeunes, les plus jeunes d’entre elles étant encore des proto-étoiles en cours de formation à partir du gaz environnant. Les astronomes regroupent ces astres en quatre classes, 0, I, II et III, selon l’intensité du leur rayonnement infrarouge émis. Plus le rayonnement infrarouge est élevé, plus l’étoile est entourée de matière froide, ce qui indique qu’elle en est encore au stade de l’effondrement gravitationnel.

Les étoiles de classe O n’ont que quelques milliers d’années et sont si jeunes qu’elles n’ont pas encore commencé le processus de fusion nucléaire. Les réactions de fusion ont commencé dans le cœur des objets de classe I, mais le gaz et la poussière continuent d’être accrétés par l’astre en formation. À ce stade, ces étoiles sont généralement encore enveloppées dans un dense nuage de gaz et de poussières, qui obscurcit la lumière visible et fait qu’elles ne peuvent être observées que dans les domaines infrarouge et radio. L’accrétion du gaz et des particules de poussière est en grande partie terminée pour les étoiles de classe II, mais elles sont toujours entourées d’un disque de gaz et poussières, tandis que les étoiles de classe III ne possèdent plus que quelques traces de leur disque d’accrétion originel.

Des études ont montré qu’environ 80 % des étoiles donnant naissance à des objets Herbig-Haro sont en fait des étoiles doubles ou multiples, cette proportion étant beaucoup plus grande que celle trouvée pour les étoiles de faible masse sur la séquence principale. Ceci semble indiquer que les systèmes binaires sont plus propices à la formation des jets qui donneront ensuite naissance aux objets HH.